Треугольный импульс
Импульс определяется выражением (рис.2.6)
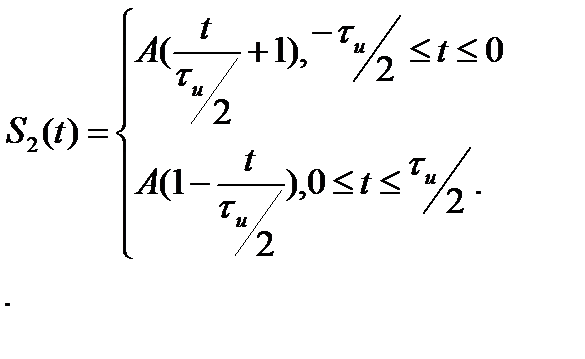
рис.2.6 рис.2.7
Применим свойства спектров. Найдем спектральную плотность функции, являющейся производной от заданного сигнала 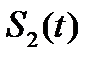 (рис.2.7)
(рис.2.7) 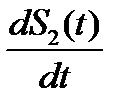 . Спектральная плотность прямоугольного импульса длительностью
. Спектральная плотность прямоугольного импульса длительностью 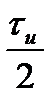 и амплитудой
и амплитудой 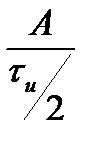 по аналогии с формулой (2.21) и с учетом сдвига середины импульса на время
по аналогии с формулой (2.21) и с учетом сдвига середины импульса на время 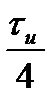 относительно точки
относительно точки 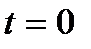 .
.
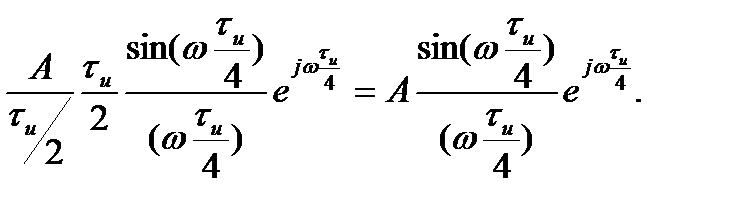
Спектральная плотность отрицательного импульса, показанного на рис.2.7, соответственно
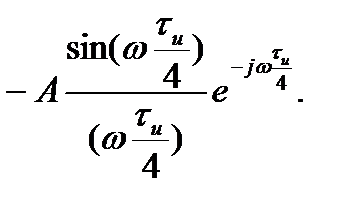
Суммарная плотность двух импульсов
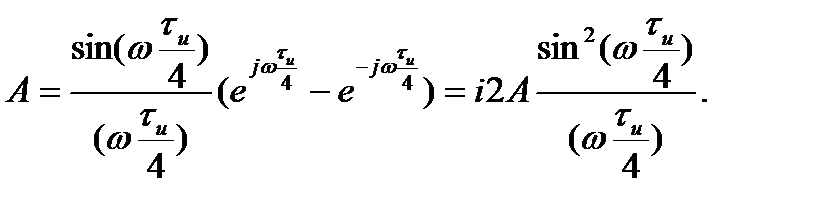
Спектральная плотность треугольного импульса, являющегося интегралом от функций 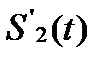 , получается делением предыдущего выражения на
, получается делением предыдущего выражения на 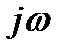 :
:
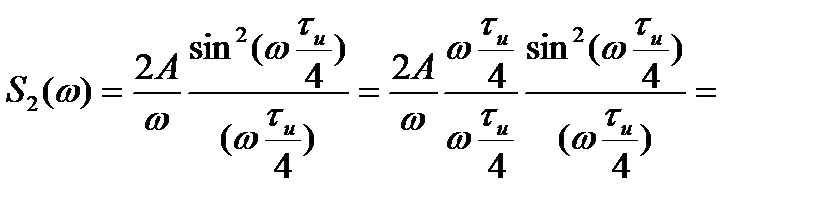
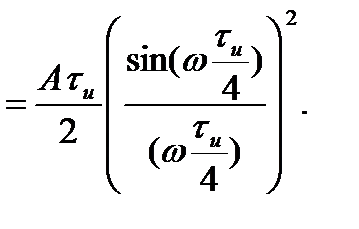 (2.22)
(2.22)
Множитель 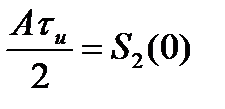 -площадь треугольного импульса. Уровень боковых лепестков спектра треугольного импульса убывает пропорционально
-площадь треугольного импульса. Уровень боковых лепестков спектра треугольного импульса убывает пропорционально 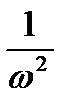 , а не на, как в случае прямоугольного импульса (рис.2.6)
, а не на, как в случае прямоугольного импульса (рис.2.6)
рис.2.6
