Информационная емкость дискретного сообщения

При описании информационных процессов часто пользуются следующими информационными характеристиками.

Производительность источника сообщений (P) — среднее количество информации, генерируемое источником в единицу времени

Единицей измерения производительности источника сообщений является бот:

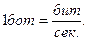
Информационная емкость сообщения (R) — это среднее количество информации, содержащееся в сообщении единичной длительности:

где I — количество информации, содержащееся в сообщении;

t – длительность сообщения.

Скорость создания (генерации) информации(Q)—это среднее количество информации, генерируемое источником сообщений за единицу времени

где W – скорость передачи символов (символ /сек);

H–среднее количество информации приходящееся на один символ (бит /символ).

Единицей измерения скорости генерации информации и информационной емкости сообщения служит бот.

В качестве примера, определим информационную емкость простейшего дискретного сообщения, состоящего из совокупности импульсов ипауз, причем длительность импульсов и пауз одинакова, а амплитуда импульсов постоянна, т.е. сообщение строится на использовании лишь двух символов (его объём алфавит равен 2).

Очевидно, если избыточность отсутствует, то на каждый символ такого сообщения приходится одна двоичная единица информации (1 бит), а на все сообщение, состоящее из n символов, приходится n бит информации.

Пусть длительность импульса ипаузы одинакова и равна 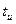, тогда длительность всего сообщения (T) будят равна

.

Из радиотехники известно, что импульсу с длительностью 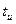соответствует определенная полоса частот Δw причем

Δw (1.12)

где k — коэффициент, зависящий от формы импульса .

Следовательно, количество информации в рассматриваемом двоичном сообщении длительностью Т не может превышать предельного значения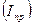

И с учетом формулы (1.12) имеем:

=T·Δw (бит).

Разделив на Т, получим предельную информационную ёмкость сообщения (R)

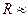Δw (бот).

Tаким образом, информационная емкость двоичного дискретного сообщения численно равна полосе частот сигнала, с помощью которого передаются символы сообщения, выраженной в герцах.

Рассмотрим дискретное сообщение состоящее из последовательности импульсов длительностью 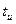, причем паузы между импульсами отсутствуют, а амплитуда каждого импульса соответствует одному из L заранее установленных дискретных уровней. Можно считать, что алфавит такого источника сообщений состоит из L равновероятных и независимых символов Количество информации в сообщении, состоящем из n таких символов (длительностью Т), не может превышать предельного значения ( ), определяемого по формуле Хартли

Δw (бит).

А информационная емкость такого сообщения (сигнала) (R) равна:

Δw

Следует отметить, что полученные выражения имеют смысл только тогда, когда разность между двумя соседними символами значительно превышает уровень помехи и когда отсутствует избыточность. В противном случае, а также в случае, когда символы, формирующие
сообщение имеют различную длительность, вычисление информационной емкости сообщения является более сложной задачей.