Мажорируемость функционального ряда

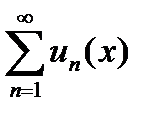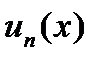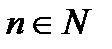Определение 6.2.6. Функциональный ряд называется мажорируемым на данном множестве Д (на котором определены функции , где ), если существует такой числовой сходящийся ряд 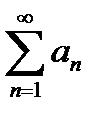с положительными членами, что члены ряда 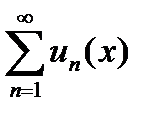(хотя бы начиная с некоторого) при всех 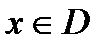не превосходят по модулю соответствующих членов ряда 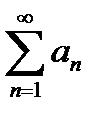, т. е.

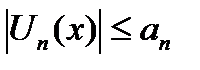
(При этом ряд 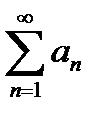называется мажорирующим или мажорантным рядом для функционального ряда).

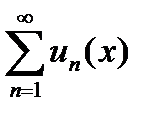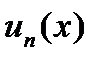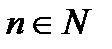! Другое определение6.2.7.Функциональный ряд (1) называется мажорируемым на данном множестве Д (на котором определены функции , где ), если существует такой сходящийся числовой ряд 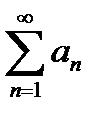(2) с положительными членами, что для всех 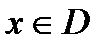выполняются соотношения

,( )

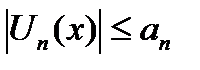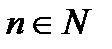Равномерная сходимость функционального ряда

Среди сходящихся функциональных рядов выделяются своей важностью так называемые равномерно сходящиеся ряды.

Определение 6.2.8. Ряд 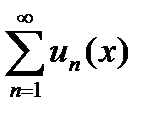(1) называется равномерно сходящимся на множестве Д, если для любого 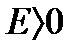можно указать такое число 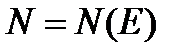, что при всех 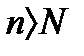будет выполнятся неравенство: 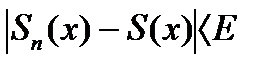для всех 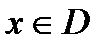(или ).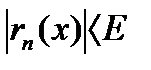

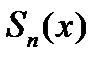- n-я частичная сумма ряда (1)

S(x)- сумма ряда (1)

Рассмотрим следующий признак, достаточный для равномерной сходимости функционального ряда.

Теорема (признак Вейерштрасса) 6.2.15.: Если функциональный ряд 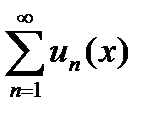(1) мажорирует на данном множестве Д, то он: 1) равномерно и 2) абсолютно сходится на этом множестве.

Пример 6.2.26.Доказать, что ряд 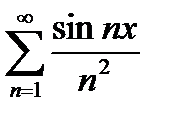сходится равномерно на всей оси ОХ.

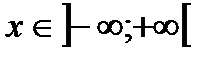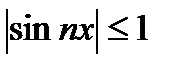Т. к. для " имеем , то 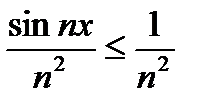( 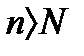). Ряд 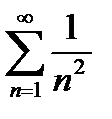сходится. По признаку Вейерштрасса данный ряд сходится равномерно на всей оси.

Замечание 6.2.8.Признак Вейерштрасса дает только достаточное условие равномерной сходимости функционального ряда, оно не является необходимым.

Замечание 6.2.9. Равномерно сходящийся в некотором промежутке ряд не обязательно сходится там и абсолютно.

Степенные ряды

Одним из важных классов функциональных рядов являются степенные ряды.

Определение 6.2.9.Функциональные ряды, членами которых являются целые положительные степени независимой переменной х или двучлена (х-х₀), ( где х₀=const), умноженные на числовые коэффициенты:

(1) 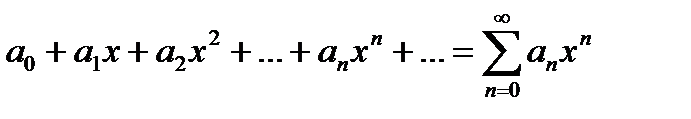, или

(2) 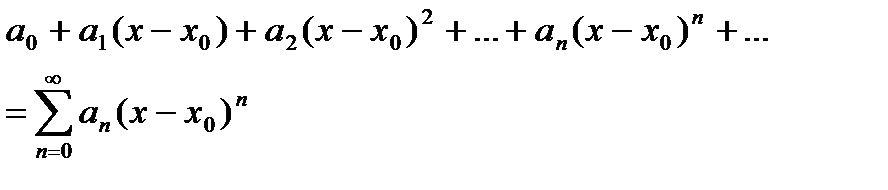называются степенными рядами.

Члены степенных рядов являются: 1) непрерывными и 2) дифференцируемыми функциями на всей числовой оси.

Ряд (1) получается из ряда (2) при х₀=0.

Все последующие рассуждения будем проводить для ряда (1), поскольку ряд (2) приводится к ряду (1) с помощью замены переменной х-х₀=Х.

Замечание 6.2.10. Для удобства n-м членом степенного ряда называют член 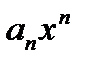, несмотря на то, что он стоит на (n+1)-м месте. Свободный член ряда a₀ считают нулевым членом.

Логически могут представиться 3 возможности:

1)ряд (1) сходится на свей числовой оси;

2)ряд сходится только в т. х=0 (в т. х=0 сходится всякий степенной ряд (1),

сумма ряда = a₀)

3) ряд сходится не только в точке х=0, но и не на всей числовой оси.