Вектори у декартовій системі координат

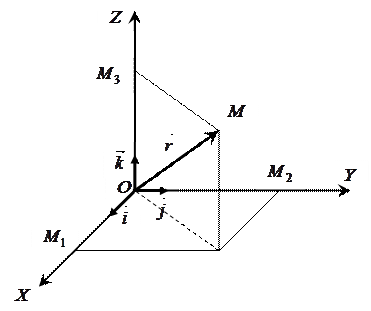
У прямокутній декартовій системі координат розглянемо довільний вектор 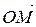(рис. .6).

Вектор 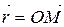називають полярним радіусом-вектором точки М. Спроектуємо цей вектор на координатні осі. Інакше кажучи, розкладемо вектор 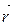на складові вектори за координатними осями. Як показано на рис. 2.6 точки 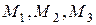– проекції точки на відповідні координатні осі.

Вектори 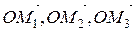– складові вектора 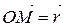за відповідними координатними осями.

Рис. 2.6

Вектор 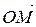є сумою векторів 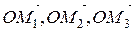, тобто

.

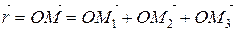(2.3)

Кожний з цих складових векторів можна надати у вигляді: 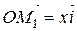, , 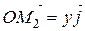, 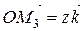де 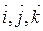– базисні вектори декартової системи координат у просторі. Підставляючи ці значення в (2.3), одержуємо:

,

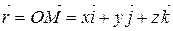(2.4)

де – скалярні величини, які називаються координатами радіус-вектора 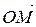у заданому базисі.

Точка має координати свого радіус-вектора 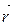, тобто 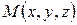. Координати точки у просторі або її радіус-вектор 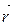однозначно вказують на її положення в просторі відносно вибраної системи координат.

Довільний вектор 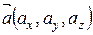можна надати у вигляді:

.

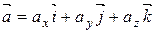(2.5)

Подання вектора у вигляді суми компонентів (2.5) називається розкладанням вектора за координатним базисом(рис. 2.7).

Довжина (модуль) вектора визначається за формулою

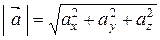.	(2.6)
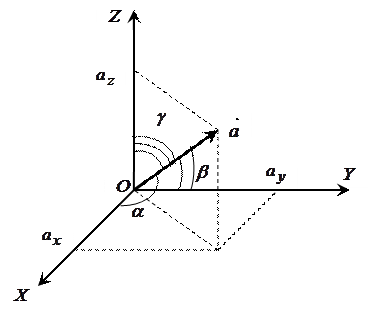Рис. 2.7

На рисунку 2.7 вектор 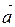утворює з координатними осям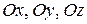и кути 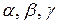відповідно. Тоді 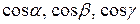називаються напрямними косинусами вектора 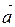. Очевидно, напрямні косинуси та модуль вектора повністю визначають положення вектора у просторі. Враховуючи властивості проекції вектора на вісь, маємо:

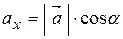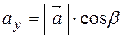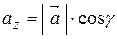, , ;	(2.7)
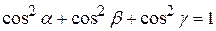	(2.8)

Лінійні операції над векторами у координатній формі:

Дано вектори та :

1) додавання та віднімання

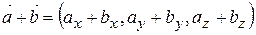;	(2.9)
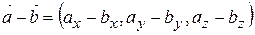;	(2.10)

2) множення вектора на скаляр

.

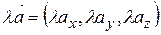(2.11)

Умови колінеарності двох векторів та визначаються співвідношенням

.

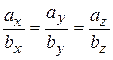(2.12)

Скалярний добуток векторів

Скалярним добутком двох векторів 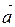та 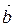(рис. 2.8) називається скаляр, який дорівнює добутку модулів цих векторів на косинус кута між ними:

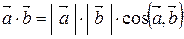.	(2.13)
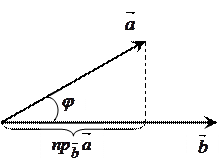Рис. 2.8

Фізичне тлумачення скалярного добутку двох векторів полягає в тому, що такий добуток являє собою роботу, виконану при переміщенні матеріальної точки під дією одного вектора вздовж другого.

Беручи до уваги властивості проекції вектора на вісь, маємо (рис. 2.9)

.

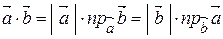(2.14)

Властивості скалярного добутку векторів:

1) ;

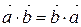2) ;

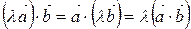3) ;

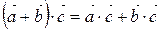4) ;

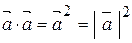5) 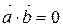, якщо ;

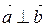6) добутки ортів , .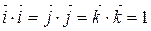

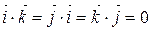Якщо вектори задані в координатній формі та , то скалярний добуток векторів можна записати у вигляді (2.15)

.

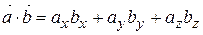(2.15)

Основні задачі, які розв’язуються з використанням скалярного добутку векторів:

1) довжина вектора

;

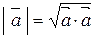(2.16)

2) косинус кута між векторами

;

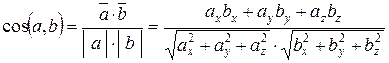(2.17)

3) проекція вектора на інший вектор

;

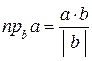(2.18)

4) умова перпендикулярності