Пример расчета переходного процесса операторным методом
Определим операторным методом uL(t) в электрической цепи, схема которой показана на рис. 6.1, если известно, что 
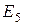= 70 В, L = 0,3 Гн, 
= 
Ф, 
Ф, 
=30 Ом, 
= 60 Ом, 
= 50 Ом.
Для подготовки задачи к решению определим независимые начальные условия из расчета установившегося режима до коммутации. Докоммутационная схема (рис. 6.2) работает при воздействии постоянной э.д.с., поэтому L представляет собой нулевое сопротивление, С – разрыв.
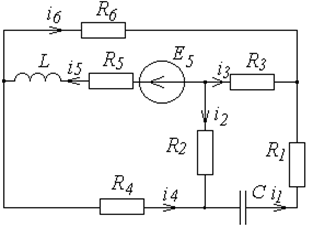 Рис. 6.1. Схема к примеру расчета цепи операторным методом |  Рис. 6.2. Схема для определения независимых начальных условий |
.
Из уравнения, составленного по 2-му закону Кирхгофа, находим
.
Откуда 
Строим эквивалентную операторную схему.
Рис. 6.3. Эквивалентная операторная схема
В операторной схеме индуктивное и емкостное сопротивления имеют вид pL и 
, в схему введены дополнительные источники, учитывающие ненулевые начальные условия 
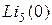и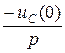 
. Вместо постоянной 
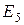появляется ее изображение 
.
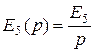Расчет построенной операторной схемы ведем любым известным методом, например, методом контурных токов.
Для выбранных на схеме рис. 6.3 контуров уравнения имеют вид:
,
.
Главный определитель системы D:
= 
.
Частный определитель 
:
= 
.
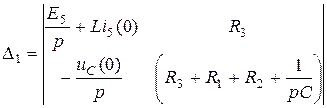При значении емкости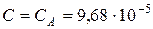 
Ф получаем:
;
= 
.
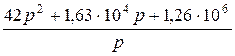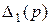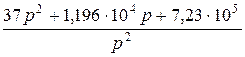Изображение контурного тока:
= 
= 
.
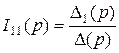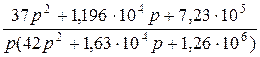Оригинал тока 
находим по теореме разложения. Корни полинома знаменателя 
. Режим, соответствующий различным отрицательным корням, апериодический.
;
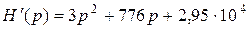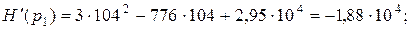
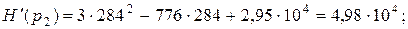
Таким образом, 
=
= 
.
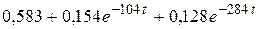Напряжение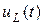 
можно вычислить как 
.
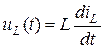Тогда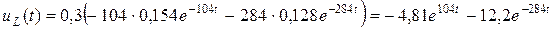 
Напряжение 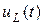можно было бы вычислить иначе, предварительно определив изображение его 
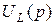по найденному изображению тока:
.
Затем от изображения 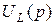перейти к оригиналу .
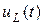Рассмотрим особенности применения операторного метода при комплексных корнях.
Для этого в приведенном выше примере изменим значение емкости. Пусть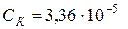 
Ф. Тогда главный определитель системы 
и частный определитель (p) подучат следующие значения:
,
= 
.
= 
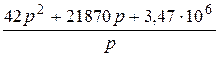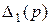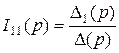Корни полинома знаменателя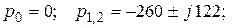 
Оригинал тока вычисляется как
=0,583+ 
=0,583+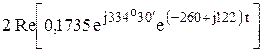 
= 
+ 
= 
.
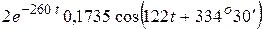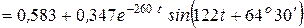Часто при наличии в схемах источников э.д.с. синусоидальной формы операторный метод используется только для расчета свободных составляющих искомых реакций. При этом принужденные составляющие рассчитываются известными методами анализа установившихся режимов.
Для нахождения изображений свободных составляющих искомых реакций составляется эквивалентная операторная схема для свободных составляющих. В этой схеме отсутствуют изображения источников тока или э.д.с., соответствующие заданным источниками тока или э.д.с. синусоидальной формы. Расчетные источники учитывают ненулевые начальные условия только свободных составляющих тока в катушке и напряжения на конденсаторе и имеют значения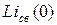 
и 
. Для вычисления 
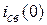и 
необходимо исходить из следующих равенств:
, 
,
, 
,
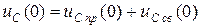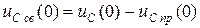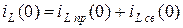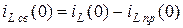где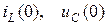 
– независимые начальные условия, найденные из расчета цепи до коммутации; 
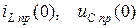– начальные значения соответствующих функций в установившемся режиме.