Замкнутые классы булевых функций

Выше показано, что любая функция может быть выражена в виде ДНФ, те. формулой, использующей функциональные знаки &,v,-> и

символы переменных Еще один интересный пример дает система функций

(1)

Выше показано, что . Используя это равенство и закон

де Моргана (свойство 11), выразим дизъюнкцию через функции

системы (1).

i

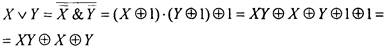
Поэтому в любой ДНФ можно выразить дизъюнкцию и отрицание через функции системы (1). Примеры:

1) = [заменяем знак отрицания] = -[заменяем знак дизъюнкции] = = [раскрываем скобки] =

2) = [заменяем знак дизъюнкции] =

3)

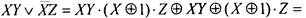
То же преобразование можно выполнить проще, заменяя сначала знак дизъюнкции

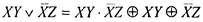. Первое слагаемое равно 0, так как

содержит произведение 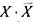, и его можно из формулы удалить

Оставшуюся часть преобразуем, заменяя знак отрицания

Как видно из рассмотренных примеров, если в формуле после произведенных замен раскрыть скобки и выполнить умножения и

сложения, а также поглощение по правилам эквивалентных преобразований, то получится формула, представляющая сумму по модулю 2 некоторых конъюнкций переменных (в каждой конъюнкции переменные не повторяются, но, в отличие от элементарных конъюнкций без отрицаний) и, быть может, константы 1

Полученная формула, порожденная логическими константами 0 и

1 и функциями называется многочленом Жегалкина

Можно показать, что различные (с точностью до перестановки слагаемых в сумме и сомножителей в конъюнкциях) многочлены представляют различные функции, т е. имеет место единственность представления булевой функции многочленом Жегалкина

В самом деле, пусть два многочлена и

равны как функции, т е на одинаковых наборах принимают одинаковые значения Тогда для какого-нибудь существенного переменного (пусть это 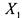), вынеся за скобки из

всех содержащих его членов, Р и Q можно представить в виде

где 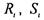- многочлены, зависящие от переменных

Достаточно показать, что 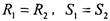как многочлены Легко

проверить, что для п = 1 утверждение о единственности многочлена верно: все функции одной переменной - в табл 5. Тем самым выполнено базовое условие для применения метода математической индукции по числу переменных п . Выполним индукционный шаг: предположим, что

утверждение справедливо для функций (л —1) переменных и докажем его для п . Поскольку Р и Q тождественно равны, то пр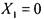и они

также равны Но при этом )

Значит, совпадают как многочлены, по предположению

индукции, и, прибавив к обеим частям (*) и, соответственно, к (**), получим

Левые части этих равенств равны, следовательно, равны и правые,

в том числе, при X = \ , откуда равны как функции. Тогда, по

предположению индукции, они совпадают и как многочлены, что завершает доказательство

Возникает вопрос' как определить для системы функций, можно ли с ее помощью выразить любую логическую функцию. В связи с этим рассмотрим несколько понятий

Замыкание системы булевых функцийD - класс всех суперпозиций функций системы D .

Примеры:1) Если система D - множество из двух функций: конъюнкции и дизъюнкции, то ее замыкание - всевозможные ДНФ такие, что входящие в них элементарные конъюнкции не содержат

*»••

отрицаний переменных (например, 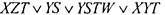). Любую

другую суперпозицию конъюнкции и дизъюнкции можно привести к такому виду: во всякой формуле, представляю'щей собой конъюнкцию дизъюнкций можно раскрыть скобки и преобразовать ее в дизъюнкцию конъюнкций. Так,

2) Если система D состоит из одной функции то ее

замыкание - всевозможные суммы различных переменных.

Замкнутый класс булевых функций- множество функций К ,

любая суперпозиция которых принадлежит К , т.е. замкнутый класс представляет собой множество булевых функций, замкнутое относительно операции суперпозиции.¹,

Примеры.1) Замыкание любой системы функций - замкнутый класс.

2) 4 функции одной переменной - замкнутый класс.

3) 2 функции 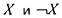образуют замкнутый класс.

4) Множество сумм по модулю 2 нечетного числа переменных является замкнутым классом, поскольку подстановка в такую функцию вместо переменной функции этого класса увеличивает число вхождений переменных в формулу на четное число; при этом некоторые слагаемые

могут взаимно сократиться ввиду эквивалентности 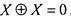, и число

переменных остается нечетным, поскольку при сокращениях в формуле переменные устраняются парами.

Упражнение.Показать, что указанные в последнем примере функции образуют замыкание системы, состоящей иэ одной функции

трех переменных

Упражнение.Проверить, является ли замкнутым класс,

содержащий все дизъюнкции переменных, состоящие из нечетного числа членов (т.е и т.д.).

Функционально полная система функций - система, замыкание которой составляет - множество всех логических функций.

Как показано выше, системы функций и

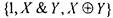полны.

Можно обобщить построения, примененные при рассмотрении полноты систем многочленов Жегалкина, и сформулировать следующее утверждение.

Пусть система - полная и пусть каждая из функций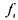

может быть выражена суперпозицией через функции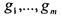

Тогда система тоже полная, потому что в формуле,

составленной из функциональных знаков системы , можно

заменить каждое вхождение символа функции на ее выражение через

символы функций

Вот несколько примеров.

(1) Система 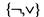полна, так как (закон деМоргана).

(2) Аналогично показывается полнота системы

(3) Система полна, поскольку