Образ и прообраз при отображении
Взятие образа
Положим,  и
и  — подмножества области определения. Взятие образа (или, что то же самое, применение оператора
— подмножества области определения. Взятие образа (или, что то же самое, применение оператора 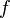 ) обладает следующими свойствами:
) обладает следующими свойствами:
· 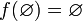 ;
;
· 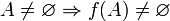 ;
;
· 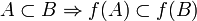 .
.
Далее
· образ объединения равен объединению образов: 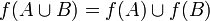 ;
;
· образ пересечения является подмножеством пересечения образов 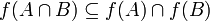 .
.
Последние два свойства, вообще говоря, допускают обобщение на любое количество множеств, большее двух (как оно здесь сформулировано).
15. Определение прообраза подмножества относительно функции. Теорема о прообразе объединения и пересечения подмножеств относительно отображения.
Взятие прообраза
Положим,  и
и  — подмножества множества
— подмножества множества  .
.
По аналогии с взятием образа, взятие прообраза (переход к прообразу) обладает также следующими двумя очевидными свойствами:
· прообраз объединения равен объединению прообразов: 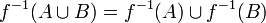 ;
;
· прообраз пересечения равен пересечению прообразов 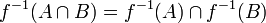 .
.
Данные свойства, также, допускают обобщение на любое количество множеств, большее двух (как оно здесь сформулировано).
В случае, если отображение обратимо (см. ниже), прообраз каждой точки области значений одноточечный, поэтому для обратимых отображений выполняется следующее усиленное свойство для пересечений:
· образ пересечения равен пересечению образов: 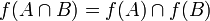 .
.
16. Определение образа и прообраза подмножества относительно функции. Теоремы об образе прообраза и прообразе образа подмножества относительно функции.
Образ и прообраз (при отображении)
Элемент 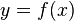 , который сопоставлен элементу
, который сопоставлен элементу 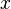 , называется образом элемента (точки)
, называется образом элемента (точки) 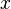 (при отображении
(при отображении 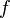 ).
).
Если взять целое подмножество  области определения функции
области определения функции 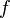 , то можно рассмотреть совокупность образов всех элементов множества
, то можно рассмотреть совокупность образов всех элементов множества  , а именно подмножество области значений (функции
, а именно подмножество области значений (функции 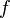 ) вида
) вида
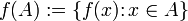 ,
,
которое, называется образом множества  (при отображении
(при отображении 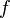 ). Это множество иногда обозначается как
). Это множество иногда обозначается как 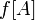 или
или 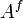 .
.
Наоборот, взяв некоторое подмножество  области значений функции
области значений функции 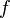 , можно рассмотреть совокупность тех элементов области определения (функции
, можно рассмотреть совокупность тех элементов области определения (функции 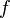 ), чьи образы попадают в множество
), чьи образы попадают в множество  , а именно — множество вида
, а именно — множество вида
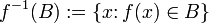 ,
,
которое называется (полным) прообразом множества  (при отображении
(при отображении 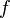 ).
).
В том частном случае, когда множество  состоит из одного элемента, скажем,
состоит из одного элемента, скажем, 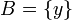 , множество
, множество 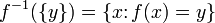 имеет более простое обозначение
имеет более простое обозначение 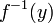 .
.
17. Свойства отображения – быть инъекцией, сюръекцией и биекцией. Теорема о композиции инъекций.
Инъективность
Основная статья: Инъекция (математика)
Функция 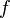 называется инъективной (или, коротко, инъекция), если разным элементам множества
называется инъективной (или, коротко, инъекция), если разным элементам множества 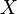 сопоставлены разные элементы множества
сопоставлены разные элементы множества 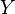 . Более формально, функция
. Более формально, функция 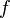 инъективна, если для любых двух элементов
инъективна, если для любых двух элементов 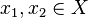 таких, что
таких, что 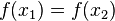 , непременно выполняется
, непременно выполняется 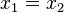 .
.
Другими словами, сюръекция — это когда «у каждого образа есть прообраз», а инъекция — это когда «разные — в разные». То есть при инъекции не бывает так, чтобы два или больше разных элементов 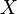 отображались в один и тот же элемент
отображались в один и тот же элемент 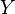 . А при сюръекции не бывает так, чтобы какой-то элемент
. А при сюръекции не бывает так, чтобы какой-то элемент 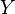 не имел прообраза.
не имел прообраза.
18. Свойства отображения – быть инъекцией, сюръекцией и биекцией. Теорема о композиции сюръекций.
Сюръективность
Основная статья: Сюръекция
Функция 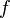 называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция
называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция 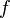 сюръективна, если образ множества
сюръективна, если образ множества 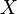 при отображении совпадает с множеством
при отображении совпадает с множеством 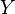 :
: 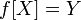 .
.
Такое отображение называется ещё отображением на.
Если условие сюръективности нарушается, то такое отображение называют отображением в.
19. Теорема о биективности отображения f:A ->B, для которого существует отображение g: B ->A с соотношениями g▫ f=1A и f ▫g =1B.
Биекция
Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением.
Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы.
Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества).
Определение
Функция 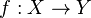 называется биекцией (и обозначается
называется биекцией (и обозначается 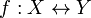 ), если она:
), если она:
1. Переводит разные элементы множества 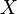 в разные элементы множества
в разные элементы множества 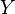 (инъективность). Иными словами,
(инъективность). Иными словами,
· 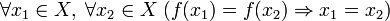 .
.
2. Любой элемент из 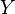 имеет свой прообраз (сюръективность). Иными словами,
имеет свой прообраз (сюръективность). Иными словами,
· 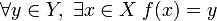 .
.
Примеры
· Тождественное отображение 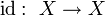 на множестве
на множестве  биективно.
биективно.
· 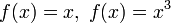 — биективные функции из
— биективные функции из 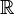 в себя. Вообще, любой моном одной переменной нечетной степени является биекцией из
в себя. Вообще, любой моном одной переменной нечетной степени является биекцией из 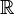 в себя.
в себя.
· 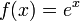 — биективная функция из
— биективная функция из 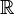 в
в 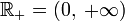 .
.
· 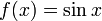 не является биективной функцией, если считать её определённой на всём
не является биективной функцией, если считать её определённой на всём 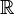 .
.
Свойства
· Функция 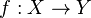 является биективной тогда и только тогда, когда существует обратная функция
является биективной тогда и только тогда, когда существует обратная функция 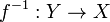 такая, что
такая, что
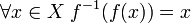 и
и 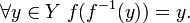
· Если функции 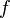 и
и 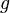 биективны, то и композиция функций
биективны, то и композиция функций 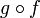 биективна, в этом случае
биективна, в этом случае 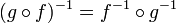 . Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если
. Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если 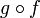 биективна, то мы можем утверждать лишь, что
биективна, то мы можем утверждать лишь, что 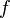 инъективна, а
инъективна, а 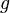 сюръективна.
сюръективна.
20. Понятие о равномощности множеств. Счетные множества. Теорема о счетности или конечности объединения счетного числа конечных множеств. Пример применения теоремы к доказательству счетности множества всех слов над конечным алфавитом.
Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощность множества — это соответствующий ему класс эквивалентности.
21. Понятие о равномощности множеств. Счетные множества. Теорема о счетности счетного объединения счетных или конечных множеств. Пример применения теоремы к доказательству счетности множества всех конечных подмножеств в множестве всех слов над конечным алфавитом.
Начнем с некоторых обозначений: через 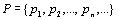 обозначим множество всех простых чисел. Нами было доказано, что Р бесконечно, кроме того, Р является подмножеством счетного множества, значит Р счетно. Обозначим через обозначим множество всех простых чисел. Нами было доказано, что Р бесконечно, кроме того, Р является подмножеством счетного множества, значит Р счетно. Обозначим через 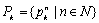 – множество всех степеней простого числа – множество всех степеней простого числа 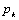 . Например . Например 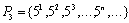 . Ясно, что для любого . Ясно, что для любого 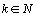 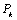 счетно и для любых i, j, счетно и для любых i, j, 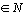 , , 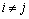 , , 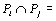 Ø. Наконец, обозначим через Ø. Наконец, обозначим через 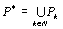 – множество всех степеней всех простых чисел. Поскольку – множество всех степеней всех простых чисел. Поскольку 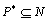 и бесконечно, то и бесконечно, то 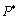 является счетным множеством. Теорема 1. Пусть является счетным множеством. Теорема 1. Пусть 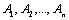 ,… – счетная совокупность счетных попарно непересекающихся множеств. Тогда множество ,… – счетная совокупность счетных попарно непересекающихся множеств. Тогда множество 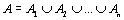 È... также является счетным. Доказательство. Так как È... также является счетным. Доказательство. Так как 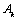 и и 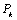 счетные множества, то существует биекция счетные множества, то существует биекция 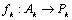 . Так как . Так как 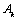 попарно не пересекаются, то семейство отображений попарно не пересекаются, то семейство отображений 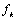 согласовано. Так как согласовано. Так как 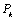 попарно не пересекаются, то попарно не пересекаются, то 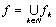 является биекцией между множествами является биекцией между множествами 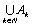 и и 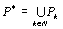 , то есть , то есть 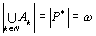 . Теорема доказана. Следствие 2. Пусть . Теорема доказана. Следствие 2. Пусть 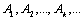 – счетная совокупность счетных или конечных множеств – счетная совокупность счетных или конечных множеств 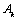 , которые попарно не пересекаются. Тогда , которые попарно не пересекаются. Тогда 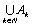 счетно. Доказательство. Легко понять, что объединение счетного числа конечных попарно пересекающихся множеств счетно. Для этого достаточно применить теорему 1, дополнив каждое конечное множество до счетного таким образом, чтобы эти расширенные множества по-прежнему попарно не пересекались. Разобьем совокупность всех данных множеств на две группы: счетно. Доказательство. Легко понять, что объединение счетного числа конечных попарно пересекающихся множеств счетно. Для этого достаточно применить теорему 1, дополнив каждое конечное множество до счетного таким образом, чтобы эти расширенные множества по-прежнему попарно не пересекались. Разобьем совокупность всех данных множеств на две группы: 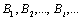 - все конечные множества исходной совокупности, - все конечные множества исходной совокупности, 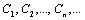 - все счетные множества исходной совокупности. Множество - все счетные множества исходной совокупности. Множество  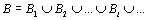 конечно или счетно, множество конечно или счетно, множество 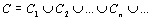 счетно, причем счетно, причем 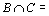 Ø. По доказанному ранее Ø. По доказанному ранее 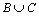 счетно. Следствие доказано. Теорема 3. Пусть счетно. Следствие доказано. Теорема 3. Пусть 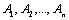 ,… – счетная совокупность счетных множеств и ,… – счетная совокупность счетных множеств и 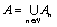 . Тогда А счетное множество. Доказательство. Построим счетную совокупность конечных или счетных попарно непересекающихся множеств, объединение которых равно А: . Тогда А счетное множество. Доказательство. Построим счетную совокупность конечных или счетных попарно непересекающихся множеств, объединение которых равно А: 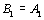 , , 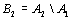 , , 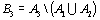 ,…, ,…, 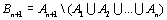 . Очевидно, что . Очевидно, что 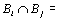 Ø при Ø при 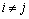 и и 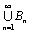 = А. По следствию 2 множество = А. По следствию 2 множество 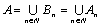 счетно. Следствие 4. Пусть счетно. Следствие 4. Пусть 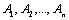 ,… – счетная совокупность конечных или счетных попарно различных множеств. Тогда множество ,… – счетная совокупность конечных или счетных попарно различных множеств. Тогда множество 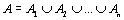 … счетно. Теорема 5. Пусть А и В счетные множества. Тогда декартово произведение … счетно. Теорема 5. Пусть А и В счетные множества. Тогда декартово произведение 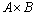 также является счетным множеством. Доказательство.Перечислим элементы множеств А и В: А= также является счетным множеством. Доказательство.Перечислим элементы множеств А и В: А= 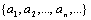 , , 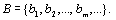 Тогда Тогда 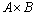 = = 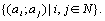 Разобьем Разобьем 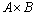 на счетное объединение счетных множеств: на счетное объединение счетных множеств: 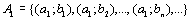 , , 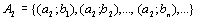 , .……………………………………. , .……………………………………. 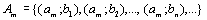 . Очевидно, что . Очевидно, что 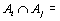 Ø при Ø при 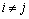 , т.к. , т.к. 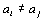 , и , и 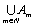 =А =А 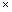 В, то есть В, то есть 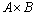 есть объединение счетного числа счетных попарно непересекающихся множеств. Значит есть объединение счетного числа счетных попарно непересекающихся множеств. Значит 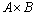 счетно. Следствие 6. Пусть счетно. Следствие 6. Пусть 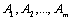 – счетные множества, тогда – счетные множества, тогда 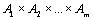 – счетно. Доказательство. Доказывается легко индукцией по m. С помощью доказанных теорем можно установить счетность некоторых общераспространенных множеств. Теорема 7.Множество рациональных чисел Q счетно. Доказательство. Множество целых чисел Z счетно, значит и множество – счетно. Доказательство. Доказывается легко индукцией по m. С помощью доказанных теорем можно установить счетность некоторых общераспространенных множеств. Теорема 7.Множество рациональных чисел Q счетно. Доказательство. Множество целых чисел Z счетно, значит и множество 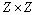 счетно. Множество Z счетно. Множество Z 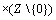 также счетно. Каждой паре (a; b), где также счетно. Каждой паре (a; b), где 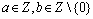 поставим в соответствие рациональное число а: b. Это отображение поставим в соответствие рациональное число а: b. Это отображение 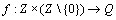 является отображением “на”, поэтому Q не более чем счетно, а так как оно бесконечно, то является отображением “на”, поэтому Q не более чем счетно, а так как оно бесконечно, то 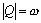 . Определение 8. а) Число . Определение 8. а) Число 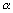 называется алгебраическим числом степени n, если называется алгебраическим числом степени n, если 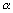 есть корень целочисленного многочлена есть корень целочисленного многочлена 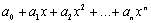 . б) Число . б) Число 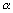 называется алгебраическим, если оно есть алгебраическое некоторой степени. Примеры. 1) Любое рациональное число а: b является алгебраическим степени 1, так как оно является корнем целочисленного уравнения называется алгебраическим, если оно есть алгебраическое некоторой степени. Примеры. 1) Любое рациональное число а: b является алгебраическим степени 1, так как оно является корнем целочисленного уравнения 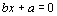 . 2) Число . 2) Число 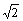 является алгебраическим числом степени 2, так как является корнем целочисленного уравнения является алгебраическим числом степени 2, так как является корнем целочисленного уравнения 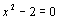 . 3) Докажем, что . 3) Докажем, что 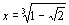 является алгебраическим числом степени 6. В самом деле, является алгебраическим числом степени 6. В самом деле, 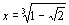 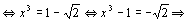 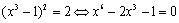 . Теорема 9.Множество алгебраических чисел счетно. Доказательство. Каждый многочлен степени n . Теорема 9.Множество алгебраических чисел счетно. Доказательство. Каждый многочлен степени n 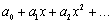 + + 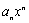 полностью определяется набором целых чисел полностью определяется набором целых чисел 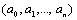 длины n+1. Поэтому целочисленных многочленов существует столько же, сколько существует таких наборов, то есть длины n+1. Поэтому целочисленных многочленов существует столько же, сколько существует таких наборов, то есть 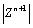 , но , но 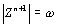 . Таким образом, целочисленных многочленов степени n существует счетное число. Пусть . Таким образом, целочисленных многочленов степени n существует счетное число. Пусть 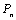 - множество всех целочисленных многочленов степени n и - множество всех целочисленных многочленов степени n и 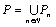 - множество всех целочисленных многочленов. Так как Р есть счетное объединение счетных множеств, то оно само счетно. Итак, множество всех целочисленных многочленов имеет счетную мощность. Перечислим все его элементы: P= - множество всех целочисленных многочленов. Так как Р есть счетное объединение счетных множеств, то оно само счетно. Итак, множество всех целочисленных многочленов имеет счетную мощность. Перечислим все его элементы: P= 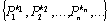 . Индекс сверху показывает степень многочлена . Индекс сверху показывает степень многочлена 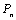 . По основной теореме алгебры многочлен . По основной теореме алгебры многочлен 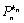 имеет имеет 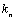 корней. Обозначим через корней. Обозначим через 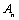 конечное множество всех корней многочлена конечное множество всех корней многочлена 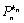 . Тогда . Тогда 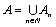 есть множество всех алгебраических чисел. Поскольку А есть счетное объединение конечных множеств, то А счетно. Теорема доказана. есть множество всех алгебраических чисел. Поскольку А есть счетное объединение конечных множеств, то А счетно. Теорема доказана. |
22. Понятие о равномощности множеств. Счетные множества. Теорема о счетности произведения счетных множеств. Доказательство счетности множества рациональных чисел.
23. Мощность континуума. Теорема Кантора о несчетности множества точек на отрезке [0;1].
24. Понятие равномощности множеств. Теорема Кантора - Бернштейна о равномощности двух множеств (без доказательства). Примеры доказательства равномощности некоторых множеств с использованием теоремы Кантора-Бернштейна (например, множества действительных чисел R и отрезка [0;1]).
