Конечные поля

Множество остатков 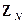с операциями сложения и умножения является коммутативным кольцом, которое часто называется кольцом вычетов по модулю .

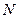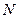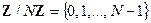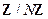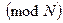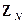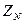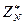Все возможные остатки от деления чисел на образуют множество . Очевидно, что - множество значений оператора модуля . Некоторые авторы обозначают это множество . Обозначим множество обратимых элементов в как , т. е. .

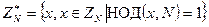Поле – это коммутативное кольцо, в котором каждый ненулевой элемент обратим.

Множество 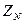является конечным полем, которое обычно называется полем вычетов по модулю 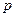и обозначается символом 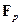. Из определения следует, что мультипликативная группа 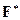поля 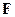совпадает с множеством 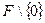. В частном случае поля вычетов получаем 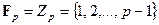и .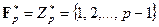

Закрепим букву 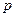за простым числом и рассмотрим множество многочленов от переменной 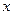с коэффициентами из 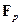. Это множество обозначается 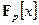и образует кольцо относительно естественных операций суммы и умножения многочленов.

Особый интерес представляет случай 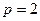. Например, в кольце 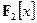выполнены равенства 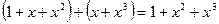и .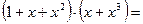

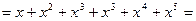
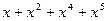Можно зафиксировать многочлен 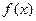и рассматривать остальные элементы кольца 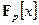по модулю 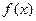, т. е. оперировать с остатками от деления многочленов на 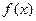. Как и натуральные числа по модулю 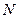, возможные остатки будут образовывать кольцо. Оно обозначается 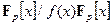или .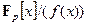

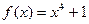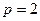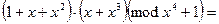
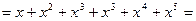
Пример. Пусть и . Тогда 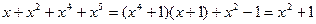, так кА все коэффициенты рассматриваются по модулю 2.

При знакомстве с целыми числами по модулю 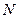нас интересовало уравнение . Можно поставить аналогичный вопрос и для многочленов.

Пусть 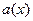, , 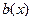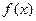- многочлены из 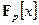. Существует ли решение уравнения 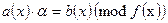. Относительно 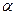? Ответ здесь, как и для чисел по модулю 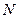зависит от наибольшего общего делителя многочленов 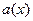и 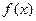. Возможны три случая. Самым интересным является случай, когда 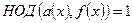, т. е. многочлены 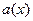и 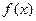взаимно простые.

Определение. Многочлен называется неприводимым, если у него нет делителей, отличных от него самого и констант.

Таким образом, неприводимость многочленов - то же самое, что и простота целых чисел. Вспомним, что целые числа по модулю 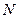образуют поле, только если 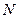- простое число. Аналогично кольцо 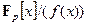является конечным полем тогда и только тогда, когда многочлен 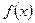неприводим.

Предположим, что 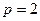и рассмотрим два неприводимых многочлена 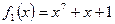и 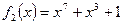. Возникают два конечных поля 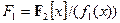и 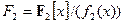, каждое из которых состоит из 2⁷ двоичных многочленов ( любой такой многочлен имеет ровно 7 коэффициентов, равных 0 или 1, поэтому всех многочленов будет 2⁷), степень которых не превосходит 6. Сложение в обоих полях выглядит одинаково, т. к. при вычислении суммы складываются коэффициенты по модулю 2. А вот умножаются элементы этих полей по-разному: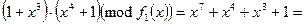 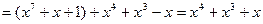и .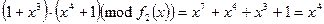

Будут ли поля 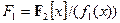и 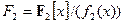действительно различны или это различие кажущееся?

Определение. Поля 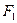и 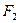называются изоморфными, если существует отображение 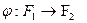, называемое изоморфизмом, которое удовлетворяет условиям: 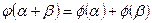и .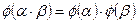

Изоморфизм существует между любыми двумя конечными полями с одинаковым числом элементов. В частности, он существует и между полям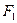и и .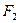

Приведенные выше конструкции по существу одинаковы и дают единственный способ построения конечных полей. Следовательно, все конечные поля фактически совпадают либо с целыми числами по простому модулю, либо с многочленами по модулю неприводимого многочлена (который тоже можно назвать простым). Также имеет место равенство 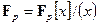. Поэтому можно утверждать единственность конструкции конечных полей. Таким образом, приходим к фундаментальной теореме о конечных полях.

Теорема. Существует единственное (с точностью до изоморфизма) конечное поле с числом элементов, равным степени простого числа.

Обозначим поле из 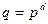элементов символом 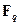или 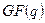(поле Галуа из элементов). Так иногда называют конечные поля

Любое конечное поле 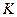содержит в себе поле целых чисел по некоторому простому модулю 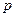. Это поле называется простым подполем поля 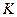. Число 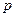элементов простого подполя называется характеристикой поля и обозначается 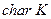. В частности, .

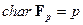На конечном поле характеристики 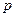можно определить так называемое отображение Фробениуса: 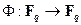, 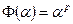. Отображение Фробениуса является изоморфизмом поля 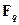с самим собой. Такие изоморфизмы называется автоморфизмами. Отображение Фробениуса замечательно тем, что множество элементов из 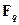, остающихся неподвижными при отображении 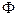, совпадает с его простым подполем, т. е. .

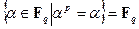Если 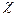- произвольный автоморфизм конечного поля, то множество неподвижных относительно него элементов тоже образует подполе, которое принято называть неподвижным полем автоморфизма 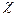. Таким образом, предыдущее утверждение говорит о том, что неподвижное поле автоморфизма Фробениуса совпадает с простым подполем .

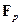Кроме того, что поле 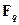содержит копию 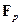можно добавить, что 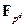содержит подполе 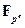для любого числа 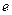, делящего 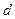. Это подполе может быть определено как неподвижное поле автоморфизма 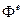, т. е.

.

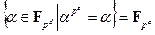Другое интересное свойство характеристики 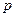поля 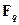заключается в том, сто взяв произвольный элемент 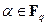и сложив его с собой 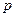раз, получим ноль. Например, в поле 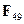имеет место равенство:

.

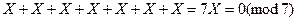Ненулевые элементы конечного поля, множество которых обычно обозначают через 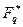составляют конечную циклическую абелеву группу. Образующая этой группы называется примитивным элементом конечного поля. Примитивный элемент есть в любом конечном поле, поскольку группа его ненулевых элементов всегда циклическая.