Гіпотеза про рівність математичних сподівань двох нормально розподілених ознак генеральної сукупності

Нехай в генеральній сукупності досліджуються дві нормально розподілені випадкові величини (ознаки) x і h з параметрами (a_x, s_x) і (a_h, s_h), відповідно. З цією метою проведено дві незалежні вибірки (x₁, x₂, ..., 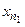) i (y_1­, y₂, ..., 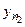_­) з об’ємами n₁ і n₂.

Необхідно перевірити таку параметричну гіпотезу:

H₀:a_x=a_h. (4.21)

Розглянемо два випадки:

а) s_x i s_h – відомі.

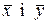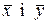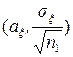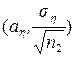Враховуючи, що значення математичних сподівань a_x i a_h випадкових величин x i h – невідомі, то для перевірки гіпотези (4.21) використовують їх точкові оцінки відповідно. Відомо [6], що, у випадку нормально розподілених x i h, вибіркові середні мають нормальний закон розподілу з параметрами i . Оскільки вибірки незалежні, то випадкові величини 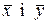також незалежні.

З цього факту випливає, що випадкова величина ( 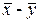) також є нормально розподіленою. Дійсно, використовуючи властивості математичного сподівання, дисперсії та їх точкових оцінок з врахуванням змісту гіпотези (4.21), будемо мати: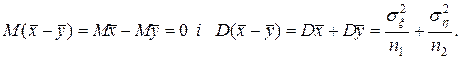

Отже, випадкова величина ( 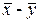) нормально розподілена з параметрами 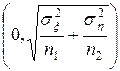. Це дає змогу зробити висновок, що оскільки випадкова величина

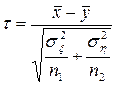, (4.22)

як неважко показати, є нормально розподіленою з параметрами (0,1), то вона може бути вибрана за міру різниці між математичними сподіваннями a_x i a_h.

При альтернативній гіпотезі 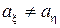для заданого рівня значущості a критичну область 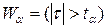можна знайти з рівняння:

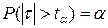. (4.23)

А оскільки 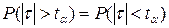, то враховуючи те, що 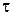– нормально розподілена випадкова величина, отримаємо, що рівняння (4.23) запишеться у вигляді:

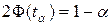, (4.24)

де 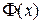– функція Лапласа.

Розв’язуючи рівняння (4.24), для заданого a за таблицею 2 у додатку для функції Лапласа отримаємо, що межа (критична точка) критичної області знаходиться в точці .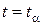

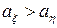
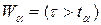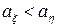
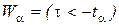При альтернативних гіпотезах: Н₁: ; Н₁: , де 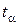– розв’язок рівняння .

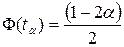Нехай 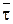– точкова оцінка випадкової величини 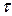, яка обчислюється на основі вибірок 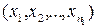і 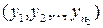за формулою (4.22). Тоді, якщо 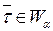, то гіпотеза відхиляється, а в протилежному випадку – приймається.

Приклад 4.13. В результаті проведення двох вибірок об’ємами n₁=40 і n₂=50 при дослідженні деякої ознаки в генеральній сукупності отримані такі середні значення: 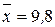і 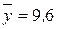. Зробивши припущення про те, що дана ознака в генеральній сукупності нормально розподілена, необхідно перевірити гіпотезу H₀: a_x=a_h, якщо відомо, що s_x=s_h=0,3 i a=0,01.

Розв’язок. За формулою (4.22), виходячи з умови задачі, знайдемо, що: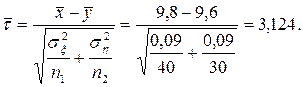

Розв’язавши рівняння (4.21), із таблиці 2 у додатку для функції Лапласа отримаємо значення межі критичної області t_0,01 = 2,58.

Оскільки 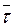>t_0,01, то, згідно із вищенаведеним критерієм, дану гіпотезу треба відхилити.

б) s_x i s_h– невідомі.

Необхідно підкреслити, що побудувати критерій узгодження для гіпотези H₀ (4.21) в загальному у даному випадку не вдається. Це складає, так звану, проблему Беренса -Фішера. Тому розглянемо лише частковий випадок, а саме: будемо вважати, що s²_x=s²_h=s², оскільки при виконанні цієї умови можна знайти випадкову величину t, як міру відхилення між математичними сподіваннями a_x i a_h.

Дійсно, можна показати, аналогічно як і в попередньому випадку, що якщо x i h - нормально розподілені випадкові величини, то випадкова величина ( 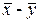) також має нормальний розподіл з параметрами 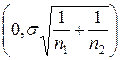. У математичній статистиці, наприклад, в [6], доведено, що, якщо за точкову оцінку дисперсії 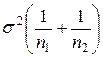вибрати наступну зміщену (це неважко показати) точкову оцінку:

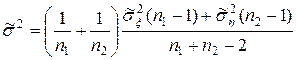,(4.25)

де 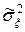i 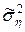- виправлені вибіркові дисперсії випадкових величин x i h, а випадкова величина ( 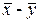) є нормально розподіленою, то випадкова величина

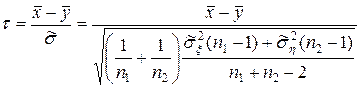(4.26)

має t - розподіл Стьюдента з 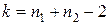числом ступенів свободи. Саме це дає змогу знайти критичну область виду 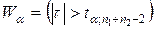, де a - рівень значущості.

Згідно з (4.2), рівняння для отримання межі (критичної точки) критичної області, виходячи з (4.26), буде мати вигляд:

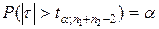. (4.27)

Розв’язуючи рівняння (4.27), для заданого рівня значущості a і числа ступенів свободи 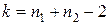за таблицею 4 для t-розподілу Стьюдента дістанемо, що межа критичної області знаходиться в точці .

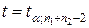А це дозволяє сформулювати шуканий критерій узгодження таким чином.

Нехай 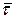– точкова оцінка випадкової величини t, яка обчислена на основі вибірок (x₁, x₂, ..., 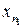) і (y₁, y₂, ..., 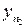) за формулою (4.26). Тоді:

1. Якщо 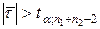, то гіпотеза H₀ відхиляється;

2. Якщо ж 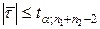, то гіпотеза H₀ приймається.

Зауваження 4.9. При перевірці гіпотези (4.18) для заданого рівня значущості a контролюється лише помилка першого роду. Задача про перевірку гіпотези про рівність математичних сподівань випадкових величин (ознак) x і h в генеральній сукупності має велике прикладне значення. Зокрема, у промисловості та торгівлі задача порівняння середніх часто виникає при вибірковому контролю якості виробів. Критерій узгодження, який сформульований у випадку б) можна застосувати до задачі про виключення грубих помилок при проведенні вибіркових спостережень.