Общее понятие о колебательном звене

Математическое описание колебательного звена выражается следующим дифференциальным уравнением, выражающим связь между выходной величиной Y и входной величиной X:

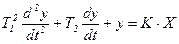, (3.79)

Переходя к изображению по Лапласу и рассматривая отношения изображений выходной и входной величин, получим передаточную функцию

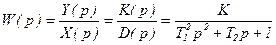, (3.80)

С подобной передаточной функцией мы уже встречались при математическом описании двигателя постоянного тока (2.41).

Так же как и звенья первого порядка, колебательное звено может быть получено путем соединения простейших звеньев. Один из вариантов показан на рисунке 3.7, а.

Дифференциальным уравнением вида (3.79) обладает колебательный контур RLC (рисунок 3.7, б). Входным сигналом цепи является напряжение U₀, а выходной величиной напряжение на конденсаторе U.

Определяя передаточную функцию как отношение изображений U(p)/U₀(p) или как отношение выходного комплексного сопротивления 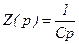к входному

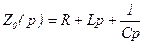, (3.81)

получим передаточную функцию (3.80) при k=1;

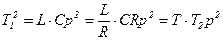, (3.82)

и

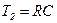, (3.83)

При рассмотрении дифференциального уравнения (3.79) становится очевидным, что динамические свойства колебательного звена зависят от соотношения постоянных времени T₁ и T₂. Для оценки этого влияния определим корни характеристического уравнения D(p)=0, т.е.

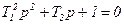, (3.84)

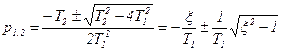, (3.85)

где x=T₂/2T₁ - коэффициент затухания (декремент затухания).

Коэффициент затухания x характеризует динамические свойства звена и является коэффициентом, связывающим постоянные времени Т₂ и Т₁. Учитывая это, удобнее уравнение колебательного звена представлять в виде:

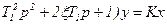, (3.86)

Из (3.84) следует, что при x<1 корни комплексные: при x=0 корни мнимые, равные; при x³1 корни вещественные.

Рассмотрим характеристики колебательного звена для этих трех случаев.

3.8 Колебательное звено (корни комплексные (x<1))

Передаточная функция

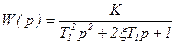, (3.87)

Представив p=jv, получим частотную передаточную функцию

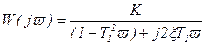, (3.88)

Разделяя на вещественную и мнимую части получим

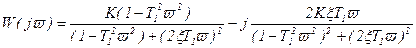,(3.89)

Амплитудно-фазовая частотная характеристика при различных x представлена на рисунке 3.7, в.

Амплитудная частотная характеристика

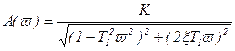, (3.90)

Фазовая частотная характеристика (рисунок 3.7, в), изменяется от 0 до -p и определяется выражением.

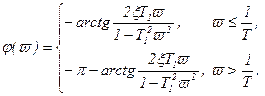, (3.91)

АЧХ и ФЧХ представлены на рисунке 3.7, г, д.

Логарифмируя выражение (3.90), получим логарифмическую амплитудную частотную характеристику

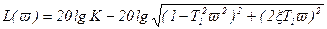, (3.92)

ЛАХ для различных значений x показаны на (рисунок 3.8, а). Видно, что асимптотическая ЛАХ может быть построена только для определенных значений x. Эти значения находятся в пределах 0,4 £ x£ 0,7.

В этом случае уравнение асимптотической ЛАХ может быть представлено в виде:

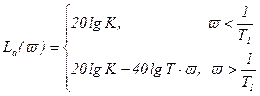, (3.93)

Асимптотическая ЛАХ при 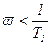параллельна оси частот, а при 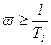имеет наклон -40 дБ/дек.

Асимптотическая ЛАХ представлена на рисунке 3.8,б, а соответствующая ей ЛФХ на рисунке 3.8, в.

Следует иметь ввиду, что при малых коэффициентах демпфирования асимптотическая ЛАХ довольно сильно отличается от точной ЛАХ. Точную ЛАХ можно построить по асимптотической, воспользовавшись кривыми отклонений точных ЛАХ от асимптотических.

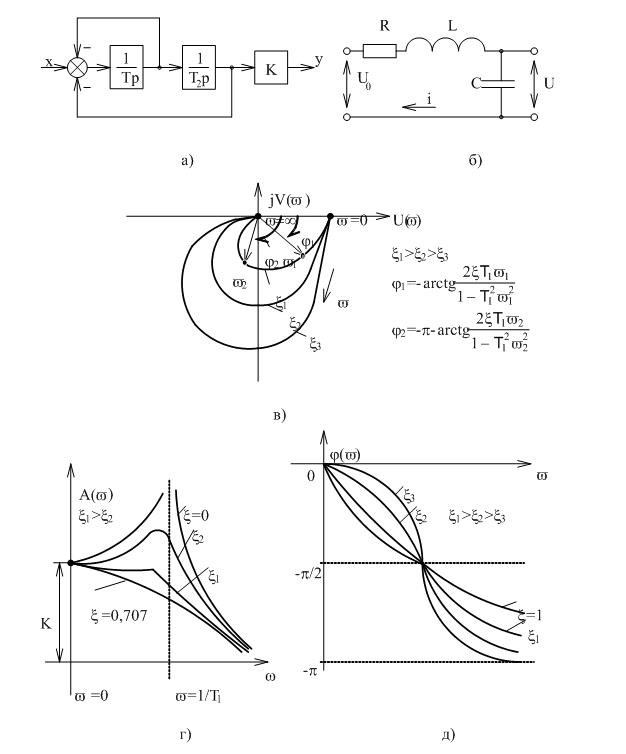
Рисунок 3.7 Частотные характеристики колебательного звена

Переходя от изображения (3.87) к оригиналу при единичном воздействии, получим переходную функцию колебательного звена:

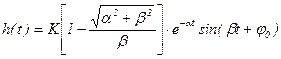, (3.94)

где

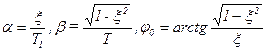, (3.95)

Весовая функция

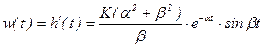, (3.96)

Переходные и весовые функции при различных значениях x представлены на рисунке 3.9, а, б.

По переходной характеристике (рисунок 3.9,а) можно определить параметры колебательного звена. Для этого необходимо знать значения амплитуд А₁ и А₂ двух соседних колебаний и период колебаний Т_к.

Тогда можно составить следующие соотношения:

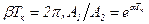, (3.97)

откуда

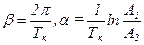, (3.98)

Параметры колебательного звена определим из выражений:

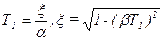, (3.99)

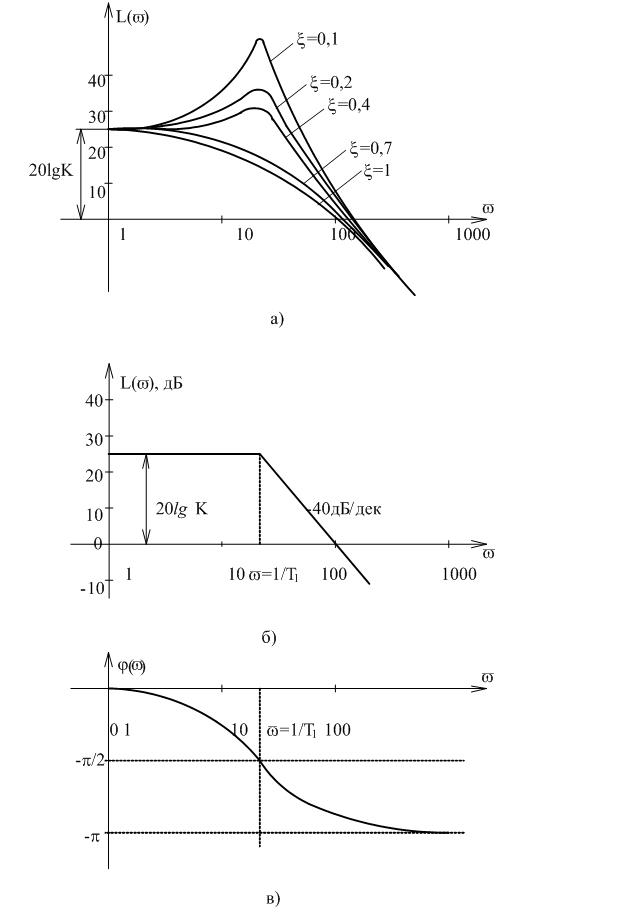
Рисунок 3.8 Логарифмические характеристики колебательного звена

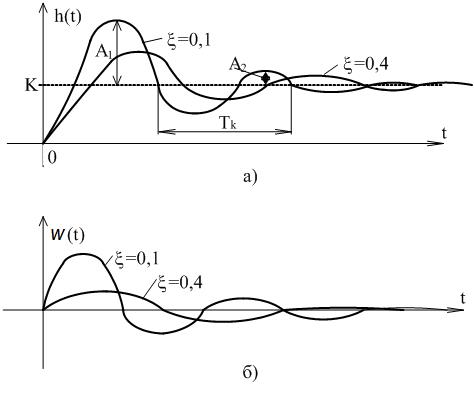
Рисунок 3.9 Временные характеристики колебательного звена

3.9 Консервативное звено (x=0)

При x=0 передаточная функция (3.87) примет вид:

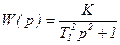, (3.100)

Частотная передаточная функция:

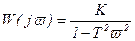, (3.101)

Из выражения (3.101) следует, что амплитудно-фазовая характеристика консервативного звена совпадает с действительной осью и начинается на вещественной оси в точке v=0 [U(v)=K] и при подходе к частоте 1/Т со стороны меньших значений уходит в бесконечность в положительном направлении действительной оси. При дальнейшем увеличении частоты характеристика возвращается из бесконечности и стремится к началу координат со стороны отрицательного направления действительной оси (рисунок 3.10, а).

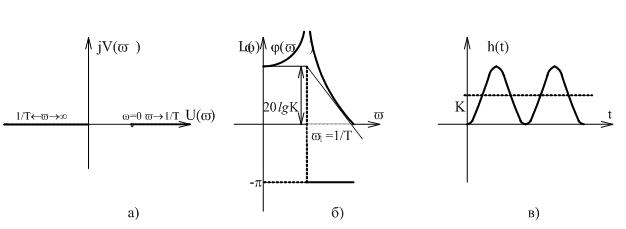
Рисунок 3.10 Характеристики консервативного звена

Таким образом, на частоте v=1/Т амплитудно-частотная характеристика консервативного звена имеет разрыв, соответствующий бесконечному возрастанию амплитуды, а фазочастотная характеристика скачком изменяет свое значение от 0 до -180°. Тогда фазочастотной характеристике можно поставить в соответствие выражение:

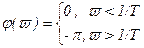, (3.102)

Графики ЛАХ и ЛФХ приведены на (рисунок 3.10, б).

Переходная функция консервативного звена характеризуется незатухающими колебаниями и описывается уравнением:

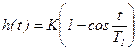, (3.103)

Переходная характеристика (рисунок 3.10, в) представляет собой график гармонических колебаний.

Производная от переходной функции, как было показано ранее, определяет импульсную переходную функцию, которая в то же время может быть определена и как оригинал, имеющий изображение в виде передаточной функции (3.100). Следовательно,

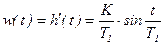, (3.104)

3.10 Апериодическое звено второго порядка (x>1)

Если 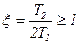, то корни характеристического уравнения отрицательные и действительные, и звено не является колебательным.

При этом выражение:

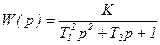, (3.105)

может быть представлено в виде:

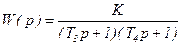, (3.106)

где

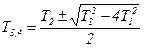, (3.107)

Очевидно, что это апериодическое звено второго порядка можно получить только при .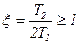

Апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка. Поэтому оно не относится к числу элементарных звеньев.