Общие теоремы динамики точки

Для решения многих задач динамики, особенно в динамике системы, вместо метода интегрирования дифференциальных уравнений движения оказывается более удобным пользоваться так называемыми общими теоремами, являющимися следствиями основного закона динамики.

Значение общих теорем состоит в том, что они устанавливают наглядные зависимости между основными динамическими характери­стиками движения материальных тел и открывают тем самым новые возможности исследования движений механических систем, широко при­меняемые в инженерной практике. Кроме того, общие теоремы позво­ляют изучать отдельные, практически важные стороны данного явле­ния, не изучая явление в целом. Наконец, применение общих теорем избавляет от необходимости проделывать для каждой задачи те опе­рации интегрирования, которые раз и навсегда производятся при выводе этих теорем; тем самым упрощается процесс решения. Сейчас мы рас­смотрим, как выглядят эти теоремы для одной материальной точки.

Количество движения (импульс) точки

Основными динамическими характеристиками движения точки являются количество движения и кинетическая энергия.

Количеством движения точки называется векторная величина равная произведению массы точки на вектор ее скорости. Направлен вектор так же, как и скорость точки, т. е. по каса­тельной к ее траектории.

Кинетической энергией (или живой силой) точки называетсяскалярная величина , равная половине произведения массы точки на квадрат ее скорости.

Необходимость введения двух динамических характеристик объяс­няется тем, что одной характеристикой нельзя охватить все особен­ности движения точки.

Например, зная количество движения автомобиля (т.е. величину Q=mv) а не величины m и v в отдельности) и действующую на него при торможении силу, можно определить, через сколько секунд автомобиль остановится, но по этим данным нельзя найти пройденный за время торможения путь. Наоборот, зная начальную кинетическую энергию автомобиля и тормозящую силу, можно определить тормоз­ной путь, но по этим данным нельзя найти время торможения.

Импульс силы

Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Введем сначала понятие об элементарном импульсе, т. е. об импульсе за бесконечно малый промежуток времени dt. Элементарным импульсом силы называется векторная величина , равная произведению вектора силы на элементарный промежуток времени dt.

.

Направлен элементарный импульс по линии действия силы.

Импульс 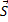любой силы 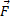за конечный промежуток времени t₁ вычисляется как интегральная сумма соответствующих элементарных импульсов:

Следовательно, импульс силы за любой промежуток времени, равен определенному интегралу от элементарного импульса, взятому в пределах от 0 до .

В частном случае, если сила и по модулю, и по направлению постоянна ( ), будем иметь . Причем, в этом случае и модуль . В общем случае модуль импульса может быть вычислен через его проекции.

Проекции импульса силы на прямоугольные декартовы оси координат равны:

.

Единицей измерения импульса в СИ является – 1 .

Пример 28.Стальной шарик массой m = 10 г, летящий со скоростью v=100 м/с по нормали к стенке, ударяется о нее и упруго отскакивает без потери скорости (рис.31). Найти импульс, полученный стенкой за время удара.

Рис.31

Решение.Из II закона Ньютона

Величина называется импульсом силы. Видно, что по модулю импульс силы равен

т.е. изменению импульса шарика.

Выберем ось х и спроецируем импульсы шарика:

Поскольку по условию задачи v₁=v₂=v, то F∆t=2mv=2∙10^-2∙10²=2 кг∙м/с.