П.4. Декартов квадрат множества.

П.1. Отображение множеств.

Определение. Пусть А и В – произвольные множества. Отображением множества А в множество В называют правило (соответствие), которое каждому элементу множества А ставит в соответствие единственный для этого элемента элемент множества В.

Обозначение. 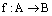. Здесь, 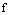– имя (наименование) отображения. Если 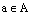– элемент множества А, то элемент множества В, который ставится ему в соответствие при этом отображении обозначают 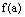и пишут 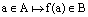. Элемент 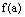называют значением отображения 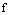"в точке а" или образом элемента а. При этом сам элемент а называют прообразом элемента .

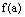Замечание. Слова отображение и функция являются синонимами, при этом множество А называют областью определения функции (отображения) 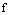и обозначают 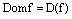, а множество значений 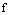обозначают 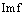и называют образом отображения 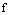. 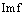является подмножеством множества В: .

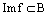П.2. Задание отображений.

Для того, чтобы определить (задать) отображение множества А в множество В нужно задать сами множества А и В, а затем задать правило с помощью которого мы сможем для каждого 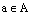находить соответствующий ему элемент 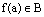. Это правило можно задать простой таблицей, если множество А конечное и имеет небольшое число элементов. Это правило можно задать с помощью формулы (математического выражения). Это правило можно задать с помощью некоторого алгоритма (процедуры). Все зависит от конкретной ситуации.

П.3. Декартово (прямое) произведение множеств.

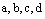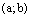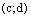Определение. Пусть – элементы каких-то множеств (не обязательно одного множества). Две пары элементов и будем называть равными и писать 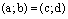, есл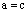и и .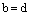

Такие пары называют упорядоченными парами, т.е. пару элементов 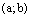называют упорядоченной парой, есл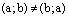и при .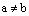

Определение. Декартовым (прямым) произведением множества А на множество В называют множество всех упорядоченных пар 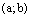, где первый элемент пары является элементом множества А, а второй – множества В и обозначается .

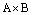Иначе, 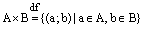. Здесь знак 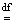означает равенство по определению.

Пример. Пусть 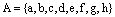– множество первых восьми букв латинского алфавита. 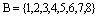– множество первых восьми натуральных чисел. Тогда декартово произведение множества А на множество В есть множество 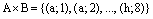. Для удобства записи все элементы этого множества можно записывать проще: 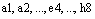и мы получаем обозначение всех 64 клеток шахматной доски.

п.4. Декартов квадрат множества.

Определение. Декартовым квадратом множества А называют декартово произведение множества А на множество А (т.е. само на себя).

Обозначение: .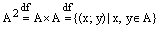

Пример. Пусть 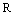– множество действительных чисел. Тогда 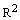– множество всех упорядоченных пар действительных чисел. Это множество можно интерпретировать как множество точек на координатной плоскости с соответствующими координатами.

3. Сочетания, размещения и перестановки из элементов множеств.

· В комбинаторике размещением называется расположение «предметов» (объектов) на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Более формально, размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных же n элементов.

Пример 1: 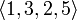— это 4-х элементное размещение из 6-ти элементного множества .

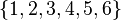Пример 2: некоторые размещения элементов множества 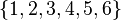по 2: ... ... ...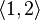

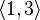
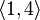
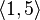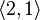
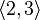
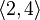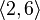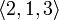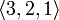В отличие от сочетаний, размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов 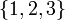(то есть совпадают как сочетания).

· перестано́вка — это упорядоченный набор чисел 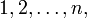обычно трактуемый как биекция на множестве 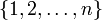, которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка.

Свойства перестановок:

· Число всех перестановок порядка 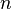равно числу размещений из n по n, то есть факториалу

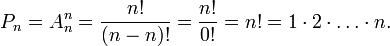
· Композиция определяет операцию произведения на перестановках одного порядка: 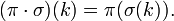Относительно этой операции множество перестановок порядка nобразует группу, которую называют симметрической и обычно обозначают .

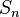· Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент 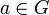сопоставляется с перестановкой 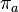, задаваемой тождеством 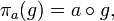где g — произвольный элемент группы G, а — групповая операция.

· сочетанием из 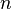по 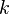называется набор 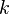элементов, выбранных из данного множества, содержащего 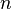различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-хэлементные сочетания, подмножества, ) {2, 1, 3} и {3, 2, 1} 6-тиэлементного множества {1, 2, 3, 4, 5, 6} ( ) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

4. Четные и нечетные перестановки.

Пусть имеется перестановка чисел 1, 2, . . . 𝑛. Мы говорим, что два числа, входящих в данную перстановку, образуют инверсию, если большее число из нашей пары предшествует меньшему. Число пар, образующих инверсию, называется числом инверсий перестановки. Минимальное число инверсий = 0 (1, 2, . . . , 𝑛)

Максимальное число инверсий = 𝐶𝑛 2 = 𝑛(𝑛−1) (𝑛, 𝑛 − 1, . . . , 3, 2, 1)

Определение. Перестановка называется четной, если

она содержит четное чилос инверсий, и называется нечетной

в противном случае.

5. Определители 2-го и 3-го порядков, вычисление, свойства.

Определителем 2-го порядка, соответствующим матрице A (или просто определителем матрицы A) называется число

detA=a11a22−a12a21.

Аналогично если квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число

detA=

a11a22a33+a21a32a13+a12a23a33−a13a22a31−a12a21a33−a21a32a11.

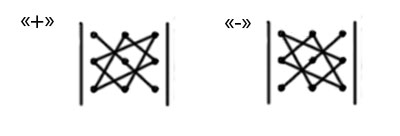Эту формулу называют "правило треугольника": одно из трех слагаемых, входящих в правую часть со знаком "+", есть произведение элементов главной диагонали матрицы, каждое из двух других - произведение элементов лежащих на параллели к этой диагонали и элемента из противоположного угла матрицы, а слагаемые, входящие в со знаком минус, строятся таким же образом, но относительно второй (побочной) диагонали.

6. Матрицы и операции над ними.

Определение: Матрицейразмера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца.

Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Основные действия над матрицами:

1) Сумма (разность) матриц.

Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

2) Умножение матрицы на число.

Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число.

3) Произведение двух матриц.

Замечание:Операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.В противном случае произведение матриц не определено.

Свойства:

1) Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение:

a(AB) = (aA)B = A(aB).

4) Транспонирование матриц:

Определение. Матрицу А^Т называют транспонированнойматрицей А, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы А^Т.(т.е. строки матрицы А заменены на столбцы и наоборот).

7. Миноры и алгебраические дополнения элементов матрицы.

Минором 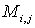элемента 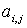матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца.

Алгебраические дополнения – это одно из понятий матричной алгебры, применяемое к элементам матрицы. Нахождение алгебраических дополнений является одним из действий алгоритма определения обратной матрицы, а также операции матричного деления.

Алгебраическим дополнением А_ij элемента а_ij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

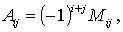
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.

Название «алгебраическое дополнение» связано с формулами разложения определителя матрицы по строке (по столбцу).

8. Обратная матрица. Условие существования, вычисление.

Матрицей, обратной матрице А, называется матрица A^-1 такая, что A^-1A = A A^-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠0 ). Это условие является и достаточным для существования A-1матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.
1. Находим определитель матрицы. Если Δ ≠0, то матрица A^-1 существует.
2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i - ой строки и j - го столбца будет алгебраическое дополнение A_ij (см. 1.3.) элемента a_ij исходной матрицы.
3. Транспонируем матрицу В и получим B^T.

Транспонировать матрицу - это значит поменять строки и столбцы местами (первый столбец с первой строкой, второй столбец со второй строкой и т. д.).
4. Найдем обратную матрицу.

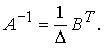
После вычисления обратной матрицы рекомендуется убедиться в том, что выполняется одна из частей условия.

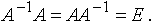
9. Ранг матрицы и каноническая форма матрицы.

Рангом системы строк (столбцов) матрицы 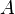с 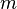строк и 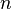столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Обычно ранг матрицы 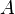обозначается 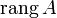( 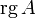) или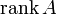

Свойства ранга матрицы:

1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы.

2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.

Квадратичная форма называется канонической, если вс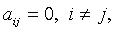е т. е.

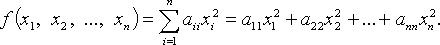
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

1. Ортогональное преобразование пространства Е_п.

2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если а₁₁ не равен 0

3. Метод Якоби (в случае, когда все главные миноры 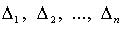квадратичной формы отличны от нуля)

10. Эквивалентность матриц и элементарные преобразования.

Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.

Надо отметить, что равные матрицы и эквивалентные матрицы - понятия совершенно различные.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

· перестановка местами любых двух строк матрицы;

· умножение любой строки матрицы на константу , ;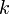

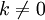· прибавление к любой строке матрицы другой строки.