Спектры периодических сигналов

СИГНАЛЫ

Под сигналом s(t) будем понимать изменение во времени одного из параметров физического процесса.

Классификация сигналов

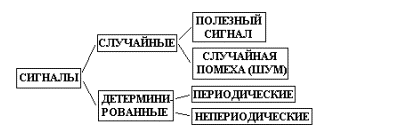
Сигналы:

- случайные

= полезный сигнал

= случайная помеха (шум)

- детерминированные

= периодические

= непериодические

Детерминированным называется сигнал, который точно определен в любой момент времени (например, задан в аналитическом виде). Детерминированные сигналы могут быть периодическими и непериодическими.

Периодическим называется сигнал, для которого выполняется условие
s(t) = s(t + kT), где k – любое целое число, Т – период, являющийся конечным отрезком времени. Пример периодического сигнала – гармоническое колебание

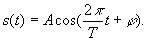
Любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с частотами, кратными основной частоте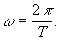

Непериодический сигнал, как правило, ограничен во времени.

Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. В качестве основных характеристик случайных сигналов принимают:

а) закон распределения вероятности (относительное время пребывания величины сигнала в определенном интервале);

б) спектральное распределение мощности сигнала.

Формы представления детерминированных сигналов

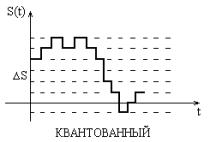
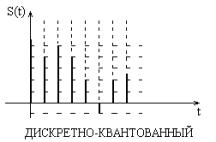
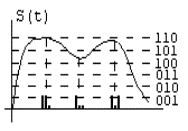
Цифровой сигналпредставляет из себя комбинацию узких импульсов одинаковой амплитуды, выражающих в двоичном виде дискретные отсчеты сигнала.

Спектры периодических сигналов

Известно, что любую функцию s(t), кусочно-непрерывную на интервале
а < t < b и ограниченную по норме , можно разложить в ряд, называемый обобщенным рядом Фурье по полному набору (базису) ортогональных функций

.

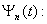
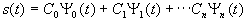(2.1)

Функции называются ортогональными, если выполняется соотношение:

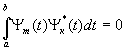при m ¹ к; 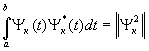- норма.

Для комплексных функций Y_k(t), Y_k^*(t) есть комплексносопряженная ей функция.

Коэффициенты ряда определяются умножением поочередно (2.1) на 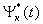и интегрированием по периоду, при этом из-за ортогональности функций справа остается только один член:

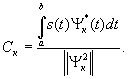(2.2)

Обобщенный ряд Фурье при заданной системе функций и при фиксированном числе слагаемых ряда обеспечивает минимум среднеквадратичной ошибки разложения:

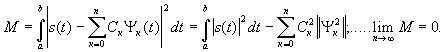
При этом говорят о среднеквадратичной, энергетической сходимости ряда к функции s(t).

Для представления периодических сигналов s(t+T) = s(t)с периодом T = b-a вне интервала a<t<b базисные функции Y_k(t) также должны быть периодическими с периодом 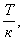k – целое число.

В радиотехнике в качестве базисных функций разложения Фурье используют преимущественно тригонометрические функции. Это объясняется следующими причинами:

а) функции cos wt, sin wt являются простыми, определены при всех значениях t, являются ортогональными и составляют полный набор при кратном уменьшении периода;

б) гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через линейную систему с постоянными параметрами, могут изменяться лишь амплитуда и фаза;

в) для гармонических функций и их комплексного анализа имеется мощный математический аппарат, найдены спектры множества форм сигналов;

г) гармоническое колебание легко осуществить на практике.

Кроме гармонического ряда Фурье применяются и другие типы разложения: по функциям Уолша, Бесселя, Хаара, полиномам Чебышева, Ляггера, Лежандра и др.

Гармонический ряд Фурье может быть представлен в следующих видах:

(2.3)

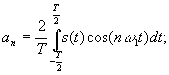
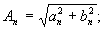
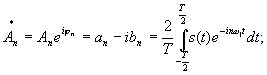
где A_n – амплитуда гармоник, nw₁ – частота гармоник, j_n – фаза гармоник,
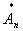- комплексная амплитуда гармоник. Все виды разложения (2.3) тождественны и переходят один в другой.

При выбранном знаке перед j_n фаза гармоник является аргументом комплексной амплитуды.

Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Одним из преимуществ разложения сигнала в спектр является следующее. Сигнал, проходя по цепи, претерпевает изменения (усиление, задержка, детектирование, изменение фазы, ограничение и т.д.). Токи и напряжения в цепи под действием сигнала описываются дифференциальными уравнениями, соответствующими элементам цепи и способу их соединения. Линейные цепи описываются линейными дифференциальными уравнениями, причем для линейных цепей верен принцип суперпозиции, согласно которому действие на систему сложного сигнала, состоящего из суммы простых сигналов, равно сумме действий от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на какой-либо простой сигнал, например, на синусоидальное колебание с определенной частотой, определить реакцию системы на любой сложный сигнал, разложив его в ряд по синусоидальным колебаниям.