Формула Ньютона – Лейбница

Пусть функция непрерывна на отрезке - некоторая первообразная функции . Тогда .

Доказательство. Из теоремы о производной интеграла по переменному верхнему пределу следует, что , т.е. 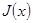- первообразная для функции . По теоремам о первообразных две первообразных отличаются на константу т.е. 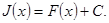Но 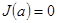(свойство 4 определенного интеграла), поэтому . Тогда . Следовательно, .

Формула Ньютона – Лейбница - это одна из немногих формул - связок, связывающих различные разделы математики воедино. Если бы не было формулы Ньютона – Лейбница, то неопределенные интегралы не нашли бы приложения, а определенные интегралы нельзя было бы вычислить аналитически. Именно эта формула делает интегральное исчисление важнейшим инструментом исследования процессов. Любой процесс описывается дифференциальными или интегральными уравнениями, а они решаются в интегралах.

Мы встречались с такими формулами или теоремами – связками. Например, теорема о связи функции, ее предела и бесконечно малой связывает бесконечно малые и пределы. Теорема Ферма и ее следствия – теоремы о средних значениях связывают дифференциальное исчисление и теорию экстремума. В дальнейшем мы тоже будем встречаться с теоремами – связками, они всегда играют фундаментальную роль, например теоремы Остроградского – Гаусса и Стокса в векторном анализе.

Методы вычисления определенного интеграла.

Методы вычисления остаются теми же, что и методы вычисления неопределенного интеграла, но разница есть. В неопределенном интеграле, делая замену переменной, надо затем возвратиться к исходной функции, в определенном интеграле этого делать не нужно, при замене пересчитываются и пределы интегрирования для новой переменной. Определенный интеграл при постоянных пределах интегрирования – число и все равно, в каких переменных считать это число. Но требование взаимной однозначности функции – замены и в определенном интеграле сохраняется, просто оно маскируется условиями теоремы о замены переменной.

Метод замены переменной.

Пусть

1) непрерывны при ,

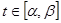1) значения 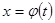, 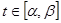не выходят за границы ,

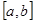2) ,

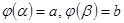Тогда

Доказательство. .

Пример .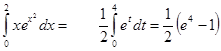

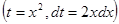
Упражнение. Найдите ошибки в применении теоремы о замене переменной.

Метод интегрирования по частям.

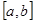Пусть функции непрерывны на . Тогда

Доказательство остается тем же, что для неопределенного интеграла, только интегрирование проводится в пределах от a до b.

Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат.

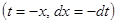
,так как

.