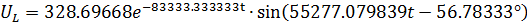Метод комплексных амплитуд

Введение

Целью данного курсового проекта является приобретение навыков определения токов, напряжений, мощностей на различных участках электрической цепи, освоить символический метод расчета электрических цепей при гармоническом внешнем воздействии, получить навыки перехода от одной формы записи комплексного числа к другой, понять физическую сущность каждой из этих форм применительно к параметрам и характеристикам электрической цепи. Уяснить порядок расчета электрической цепи в переходном режиме классическим и операторным методами. Научиться определят начальные условия и принужденные составляющие токов и напряжений, при расчете операторным методом освоить применение формул разложения.

Теоретические основы расчета цепей синусоидального тока.

Синусоидальный ток

Синусоидальным током называют ток, изменяющийся во времени по синусоидальному закону.

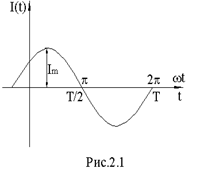
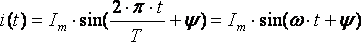
Ток i(t) называют мгновенным. Максимальное значение тока называют амплитудой и обозначают 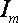. Период 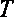– это время, за которое совершается одно полное колебание. Частота равна числу колебаний в секунду 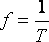, единица частоты 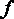- герц (Гц).

Угловая частота 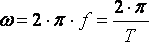, единица угловой частоты рад/с или 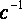. Аргумент синуса, т.е. 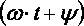, называют фазой. Фаза характеризует состояние колебания в данный момент времени .

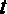Начальная фаза тока - .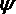

Любая синусоидальная функция характеризуется тремя величинами: амплитудой, угловой частотой и начальной фазой.

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи.

Метод комплексных амплитуд

Метод комплексных амплитуд — метод расчета линейных электрических цепей, содержащих реактивные элементы, в установившемся режиме при гармонических входных сигналах.

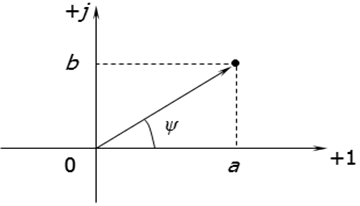
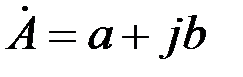Возможны три формы записи комплексного числа.

(алгебраическая форма)

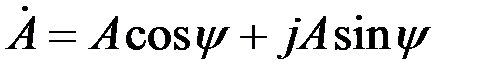(тригонометрическая форма)

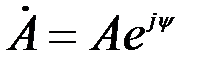
(показательная форма)

Суть метода заключается в следующем:

Для всех реактивных элементов определяется их комплексный импеданс (комплексное сопротивление двухполюсника для гармонического сигнала.).

Все токи и напряжения рассматриваются в виде комплексных амплитуд.

После введения этих замен задача анализа цепи сводится к задаче анализа цепи на постоянном токе:

импедансы трактуются как обычные сопротивления

комплексные амплитуды токов и напряжений как обычные токи и напряжения

Таким образом, мы избавились от реактивности элементов и зависимости от времени сигналов. Эти факторы, затрудняющие математическое описание схемы, теперь перенесены в сигнал: все параметры зависят от частоты гармонического сигнала и являются комплекснозначными.

Задача анализа цепи на постоянном токе решается соответствующими методами, например, методом узловых потенциалов или методом контурных токов. После нахождения всех искомых комплексных амплитуд их можно при необходимости перевести обратно в гармонические сигналы.

Переходные процессы

2.1.Законы коммутации:

Первый закон коммутации

Ток в индуктивности не может меняться скачком, поэтому мгновенное значение тока в ветви с индуктивностью в первый момент переходного процесса остается таким же, каким было в последний момент предшествующего установившегося режима.

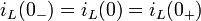
Второй закон коммутации

Напряжение на емкости не может изменяться скачком, поэтому мгновенное значение напряжения на емкости в первый момент переходного процесса остается таким же, каким было в последний момент предшествующего установившегося режима.

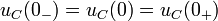
2.2.Методы расчёта переходных процессов:

Классический метод — использует решение дифференциальных уравнений с постоянными параметрами методами классической математики.

Операторный метод — перенос расчёта переходного процесса из области функций действительной переменной (времени t) в область функций комплексного переменного, в которой дифференциальные уравнения преобразуются в алгебраические.

Классический метод расчёта переходных процессов

Название метода «классический» отражает использование в нем решений дифференциальных уравнений с постоянными параметрами методами классической математики. Данный метод обладает физической наглядностью и удобен для расчета простых цепей (расчет сложных цепей упрощается операторным методом).

Расчет выполняется следующим образом.

Найти независимые начальные условия, то есть, напряжения на ёмкостях и токи на индуктивностях в момент начала переходного процесса.

Далее необходимо составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение, в общем случае неоднородное относительно искомого тока или напряжения. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе.

Далее следует составить общее решение полученного неоднородного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения.

Наконец, в общем решении следует найти постоянные интегрирования из начальных условий, т. е. условий в цепи в начальный момент времени после коммутации.

Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают установившийся режим в рассматриваемой цепи (если он существует), т. е. постоянные токи и напряжения, если в цепи действуют источники постоянных ЭДС и токов, или синусоидальные напряжения и токи при действии источников синусоидальных ЭДС и токов. Токи и напряжения установившегося режима называют установившимися.

Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который поэтому называют свободным процессом. Токи и напряжения свободного процесса называют свободными, а их выражения должны содержать постоянные интегрирования, число которых равно порядку однородного уравнения.

Операторный метод расчёта переходных процессов

Операторный метод — это метод расчёта переходных процессов в электрических цепях, основанный на переносе расчёта переходного процесса из области функций действительной переменной (времени t) в область функций комплексного переменного (либо операторной переменной), в которой дифференциальные уравнения преобразуются в алгебраические.

Прямое преобразование Лапласа:

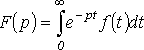
Обратное преобразование Лапласа:

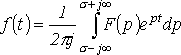
Преобразование функций действительного переменного в операторную функцию производится с помощью методов операционного исчисления. Например, если в цепи имеется источник постоянной ЭДС 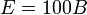, то в операторной схеме замещения вместо неё будет операторная ЭДС .

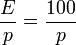Последовательность расчёта операторным методом:

1. Определяются независимые начальные условия;

2. Вычерчивается операторная схема замещения, при этом электрические сопротивления заменяются эквивалентными операторными сопротивлениями, источники тока и источники ЭДС заменяются соответствующими операторными ЭДС, при этом следует учесть, что на месте реактивных сопротивлений помимо операторных сопротивлений появляются дополнительные операторные ЭДС;

3. Находятся операторные функции токов и напряжений в цепи одним из методов расчёта электрической цепи с помощью решения обыкновенных алгебраических уравнений и их систем;

4. Производится преобразование найденных операторных функций токов и напряжений в функцию действительного переменного с помощью методов операционного исчисления.

Операторный метод позволяет производить расчёт сложных схем менее трудоёмко, чем классический метод.

Вариант 24

1. Расчет электрической цепи при гармоническом воздействии.

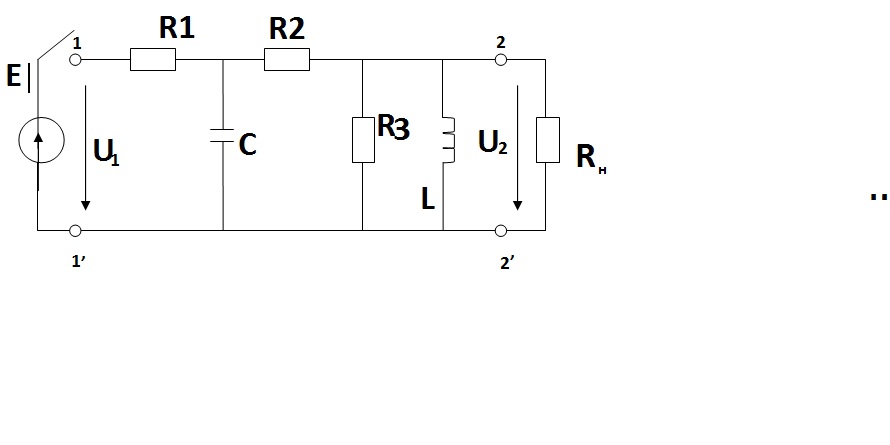
1.Определим угловую частоту:

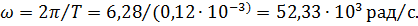
2.Находим реактивные сопротивления:

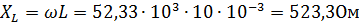
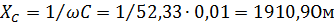
3.Методом свертывания определим общее комплексное сопротивление цепи:

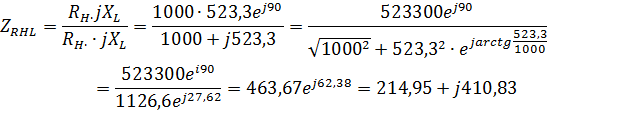
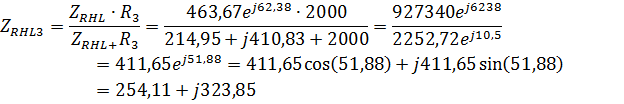
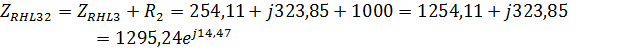
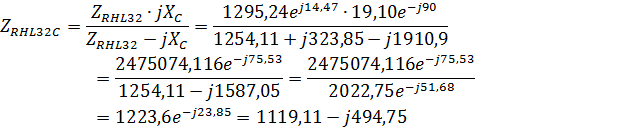
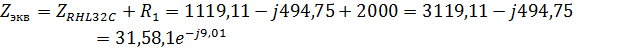
4.Найдем токи и напряжения:

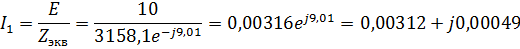
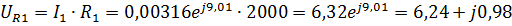
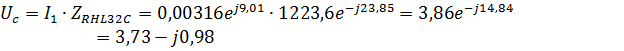
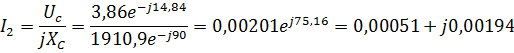
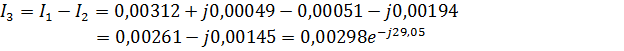
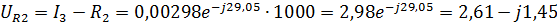
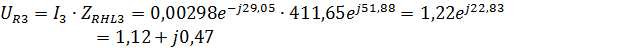
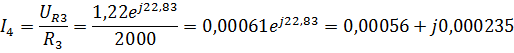
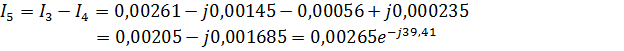
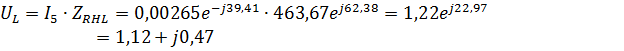
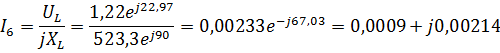
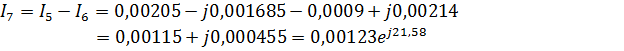
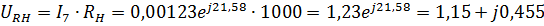
Мгновенные значения токов и напряжений:

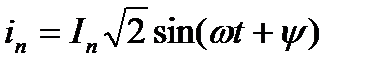
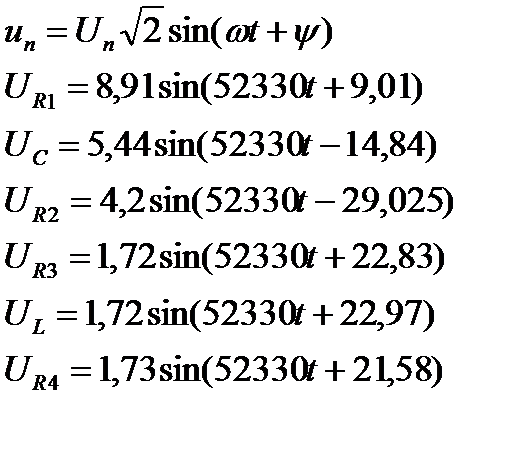
Баланс мощностей:

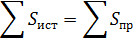
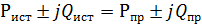
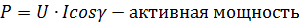
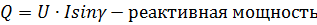
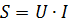
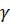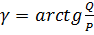
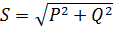Q S

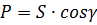
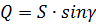
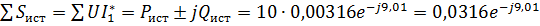=0,03121-j0,00494

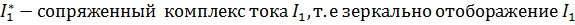
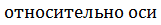
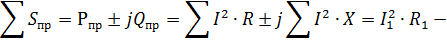
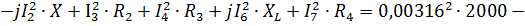
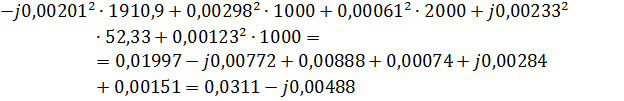
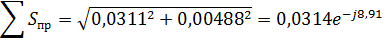
II.часть

Расчет переходных процессов.

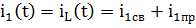
В установившемся режиме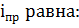

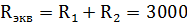
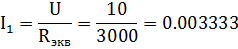
Свободная составляющая:

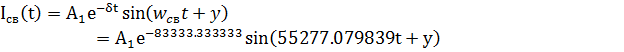
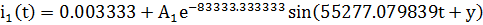
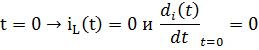
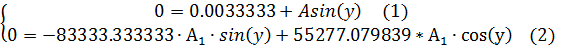
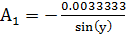, подставим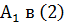

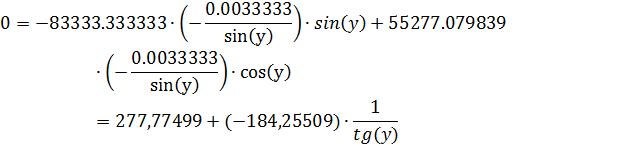
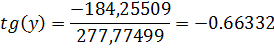
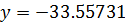
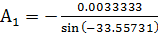=-0.00603