Примеры решения задач по множественной регрессии

Пример 1. Уравнение регрессии, построенное по 17 наблюдениям, имеет вид:

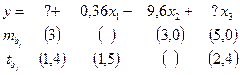
Расставить пропущенные значения, а также построить доверительный интервал для b₂ с вероятностью 0,99.

Решение. Пропущенные значения определяем с помощью формул:

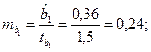
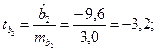
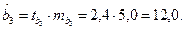
Таким образом, уравнение регрессии со статистическими характеристиками выглядит так:

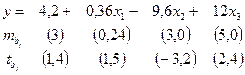
Доверительный интервал для b₂ строим по соответствующей формуле. Здесь уровень значимости равен 0,01, а число степеней свободы равно n – p – 1 = 17 – 3 – 1 = 13, где n = 17 – объём выборки, p = 3 – число факторов в уравнении регрессии. Отсюда

,

или 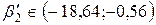. Этот доверительный интервал накрывает истинное значение параметра 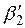с вероятностью, равной 0,99.

Пример 2.Уравнение регрессии в стандартизованных переменных выглядит так:

.

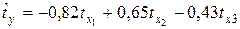При этом вариации всех переменных равны следующим величинам:

.

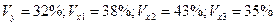Сравнить факторы по степени влияния на результирующий признак и определить значения частных коэффициентов эластичности.

Решение.Стандартизованные уравнения регрессии позволяют сравнивать факторы по силе их влияния на результат. При этом, чем больше по абсолютной величине коэффициент при стандартизованной переменной, тем сильнее данный фактор влияет на результирующий признак. В рассматриваемом уравнении самое сильное воздействие на результат оказывает фактор х₁, имеющий коэффициент – 0,82, самое слабое – фактор х₃ с коэффициентом, равным – 0,43.

В линейной модели множественной регрессии обобщающий (средний) коэффициент частной эластичности определяется выражением, в которое входят средние значения переменных и коэффициент при соответствующем факторе уравнения регрессии натурального масштаба. В условиях задачи эти величины не заданы. Поэтому воспользуемся выражениями для вариации по переменным:

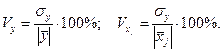
Коэффициенты b_j связаны со стандартизованными коэффициентами β_j соответствующим соотношением, которое подставим в формулу для среднего коэффициента эластичности:

.

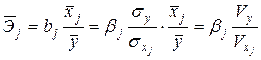При этом знак коэффициента эластичности будет совпадать со знаком β_j:

■

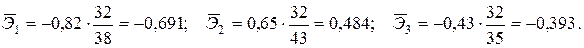
Пример 3. По 32 наблюдениям получены следующие данные:

Определить значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра а.

Решение. Значение скорректированного коэффициента детерминации определим по одному из формул для его вычисления:

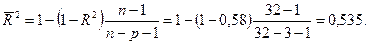
Частные коэффициенты эластичности (средние по совокупности) вычисляем по соответствующим формулам:

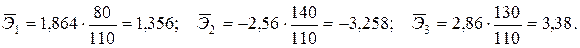
Поскольку линейное уравнение множественной регрессии выполняется при подстановке в него средних значений всех переменных, определяем параметр а:

■

Пример 4. По некоторым переменным имеются следующие статистические данные:

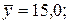
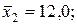
Построить уравнение регрессии в стандартизованном и натуральном масштабах.

Решение.Поскольку изначально известны коэффициенты парной корреляции между переменными, начать следует с построения уравнения регрессии в стандартизованном масштабе. Для этого надо решить соответствующую систему нормальных уравнений, которая в случае двух факторов имеет вид:

или, после подстановки исходных данных:

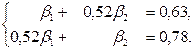
Решаем эту систему любым способом, получаем: β₁ = 0,3076, β₂ = 0,62.

Запишем уравнение регрессии в стандартизованном масштабе:

Теперь перейдем к уравнению регрессии в натуральном масштабе, для чего используем формулы расчета коэффициентов регрессии через бета-коэффициенты и свойство справедливости уравнения регрессии для средних переменных:

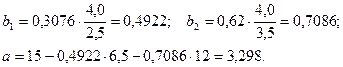
Уравнение регрессии в натуральном масштабе имеет вид:

■

Пример 5.При построении линейной множественной регрессии по 48 измерениям коэффициент детерминации составил 0,578. После исключения факторов х₃, х₇ и х₈ коэффициент детерминации уменьшился до 0,495. Обоснованно ли было принятое решение об изменении состава влияющих переменных на уровнях значимости 0,1, 0,05 и 0,01?

Решение.Пусть 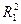- коэффициент детерминации уравнения регрессии при первоначальном наборе факторов, 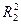- коэффициент детерминации после исключения трех факторов. Выдвигаем гипотезы:

;

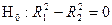Основная гипотеза предполагает, что уменьшение величины 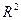было несущественным, и решение об исключении группы факторов было правильным. Альтернативная гипотеза говорит о правильности принятого решения об исключении.

Для проверки нуль – гипотезы используем следующую статистику:

,

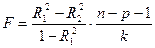где n = 48, p = 10 – первоначальное количество факторов, k = 3 – количество исключаемых факторов. Тогда

Сравним полученное значение с критическим F(α; 3; 39) на уровнях 0,1; 0,05 и 0,01:

F(0,1; 3; 37) = 2,238;

F(0,05; 3; 37) = 2,86;

F(0,01; 3; 37) = 4,36.

На уровне α = 0,1 F_набл > F_кр, нуль – гипотеза отвергается, исключение данной группы факторов не оправдано, на уровнях 0,05 0,01 нуль – гипотеза не может быть отвергнута, и исключение факторов можно считать оправданным.

■

Пример 6. На основе квартальных данных с 2000 г. по 2004 г. получено уравнение 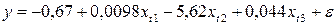. При этом ESS=110,3, RSS=21,4 (ESS – объясненная СКО, RSS – остаточная СКО). В уравнение были добавлены три фиктивные переменные, соответствующие трем первым кварталам года, и величина ESS увеличилась до 120,2. Присутствует ли сезонность в этом уравнении?

Решение. Это задача на проверку обоснованности включения группы факторов в уравнение множественной регрессии. В первоначальное уравнение с тремя факторами были добавлены три переменные, соответствующие первым трем кварталам года.

Определим коэффициенты детерминации уравнений. Общая СКО определяется как сумма факторной и остаточной СКО:

ТSS = ESS₁ + RSS₁ = 110,3 + 21,4 = 131,7

Отсюда:

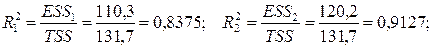
Проверяем гипотезы . Для проверки нуль – гипотезы используем статистику

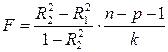
Здесь n = 20 (20 кварталов за пять лет – с 2000 г. по 2004 г.), p = 6 (общее количество факторов в уравнении регрессии после включения новых факторов), k = 3 (количество включаемых факторов). Таким образом:

Определим критические значения статистики Фишера на различных уровнях значимости:

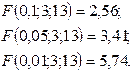
На уровнях значимости 0,1 и 0,05 F_набл> F_кр, нуль – гипотеза отвергается в пользу альтернативной, и учет сезонности в регрессии является обоснованным (добавление трех новых факторов оправдано), а на уровне 0,01 F_набл< F_кр, и нуль – гипотеза не может быть отклонена; добавление новых факторов не оправдано, сезонность в регрессии не является существенной.

■

Пример 7. При анализе данных на гетероскедастичность вся выборка была после упорядочения по одному из факторов разбита на три подвыборки. Затем по результатам трехфакторного регрессионного анализа было определено, что остаточная СКО в первой подвыборке составила 180, а в третьей – 63. Подтверждается ли наличие гетероскедастичности, если объем данных в каждой подвыборке равен 20?

Решение. Рассчитаем–статистику для проверки нуль–гипотезы о гомоскедастичности по тесту Голдфелда–Квандта:

.

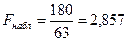Найдем критические значения статистики по Фишеру:

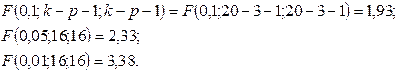
Следовательно, на уровнях значимости 0,1 и 0,05 F_набл> F_кр, и гетероскедастичность имеет место, а на уровне 0,01 F_набл< F_кр, и гипотезу о гомоскедастичности отклонить нельзя.

■

Пример 8. На основе квартальных данных получено уравнение множественной регрессии 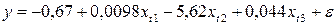, для которого ESS = 120,32 и RSS = 41,4. Для этой же модели были раздельно проведены регрессии на основе следующих данных: 1 квартал 1991 г. – 1 квартал 1995 г. и 2 квартал 1995 г. – 4 квартал 1996 г. В этих регрессиях остаточные СКО соответственно составили 22,25 и 12,32. Проверить гипотезу о наличии структурных изменений в выборке.

Решение. Задача о наличии структурных изменений в выборке решается с помощью теста Чоу.

Гипотезы имеют вид: 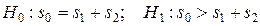, где s₀, s₁ и s₂ – остаточные СКО соответственно для единого уравнения по всей выборке и уравнений регрессии двух подвыборок общей выборки. Основная гипотеза отрицает наличие структурных изменений в выборке. Для проверки нуль – гипотезы рассчитывается статистика (n = 24; p = 3):

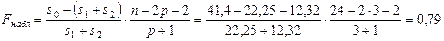
Поскольку F – статистика меньше единицы, нуль – гипотезу нельзя отклонить ни для какого уровня значимости. Например, для уровня значимости 0,05 :

.

■
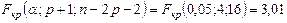