Для исследования функции в критических точках сформулируем достаточное условие экстремума функции двух переменных. Следующую теорему примем без доказательства

Теорема 2.2 (достаточное условие экстремума). Пусть функция 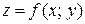имеет непрерывные частные производные до третьего порядка включительно в некоторой области, содержащей стационарную точку 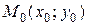. Вычислим в точке 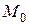значения . Обозначим

.

Тогда:

1. если , то функция 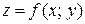имеет экстремум в точке :

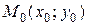§ максимум, если ;

§ минимум, если ;

2. если , то функция 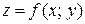не имеет экстремума в точке ;

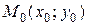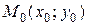3. если , то экстремум в точке может быть, а может и не быть. Необходимы дополнительные исследования.

Пример 2.1. Найти экстремум функции .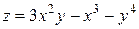

Решение. 1) Найдем частные производные первого порядка:

.

Чтобы найти стационарные (критические) точки, составляем и решаем систему уравнений:

Û или .

Таким образом, получаем две стационарные точк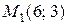и и .

2) Находим частные производные второго порядка:

.

Исследуем характер каждой стационарной точки.

а) В точке 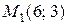имеем

Тогда

.

Так как , то в точке функция имеет локальный максимум.

.

б) В точке имеем

.

Тогда . Проведем дополнительное исследование. Значение функции в точке равно нулю, т.е. . Можно заметить, что при ; при . Значит, в окрестности точки функция принимает как отрицательные, так и положительные значения. Следовательно, в точке функция экстремума не имеет.

Неопределенный интеграл и его свойства.

Определение. Неопределенным интегралом f(x)dx называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. $ \int f(x)dx=F(x)+C,$ или $ d(F(x)+C)=f(x)dx.$ Функцию $ F(x)$ называют первообразной функции $ f(x)$ . Первообразная функции $ f(x)$ определяется с точностью до постоянной величины.

Свойства неопределенного интеграла

Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если , то

Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению

Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы

Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов

Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов

Свойство 6. Постоянный множитель можно выносить за знак интеграла

Свойство 7. Если

то

Таблица интегралов.

8. Методы интегрирования неопределенного интеграла: непосредственное, подстановки, по частям, разложение дроби на простейшие, тригонометрических функций.