Определение динамических характеристик элементов систем по временным характеристикам

Для исследования процессов в реальных системах пользуются идеализированными схемами, которые точно описываются математически и приближенно характеристики реальных объектов.

Независимо от назначения объектов, физических принципов действия и т.д. можно выделить ряд типовых звеньев, описываемых обыкновенными дифференциальными уравнениями первого или второго порядков:

- простейшие (пропорциональные, интегрирующие и дифференцирующие);

- звенья первого порядка (инерционные, инерционно-дифференцирующие, форсирующие и инерционно-форсирующие);

- колебательные звенья второго порядка.

Введение типовых звеньев удобно для представления сложного звена с передаточной функцией

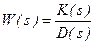(4.1)

параллельным или последовательным соединением типовых звеньев.

Передаточные функции типовых звеньев представляют собой рациональную дробь вида (4.1), причем нули и полюса функции 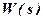, соответствующие уравнениям

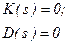, (4.2)

лежат в левой полуплоскости s или на ее границе, совпадающей с мнимой осью.

Зависимость изменения выходных координат от изменения входных может быть описана математической моделью [3], в которые входят:

- уравнения статики;

- уравнения динамики.

4.2.1. Определение статических характеристик

Уравнения статики описывают установившееся состояние координат объекта, когда

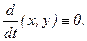(4.3)

Уравнения статики представляют собой алгебраические зависимости.

Статической характеристикой объекта называется зависимость

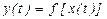
или

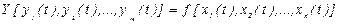
между входной и выходной координатами на отрезке времени, когда все производные входа и выхода равны нулю: .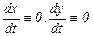

На практике чаще всего определяют статические характеристики отдельно каждой координаты выхода от каждой отдельной входной координаты 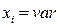при постоянных значениях остальных входных 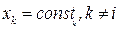вида .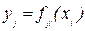

Схема снятия характеристики представлена на рисунке 4.1.

Для экспериментального определения статических зависимостей применяют активный и пассивный методы исследования.

Активный метод

Метод включает несколько этапов.

1. Испытатель выбирает одну их входных координат j объекта (если их несколько) 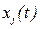и устанавливает минимально возможное по технологическому регламенту значение этой координаты.

(Все остальные входные координаты при этом поддерживаются постоянными).

Этому значению дается обозначение 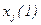. После окончания переходных процессов в объекте регистрируется установившееся значение выходной координаты 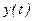, которому присваивается номер .

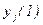2. Затем экспериментатор дает приращение 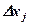входной координате 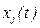, получает новое ее значение 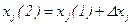, регистрирует .

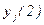3. Снова изменяет 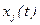на 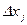и т.д.

В результате серии опытов получают таблицу соответствий

где n - число различных уровней входной координаты .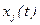

4. По данным таблицы строится график, который аппроксимируется кусочно-линейной зависимостью.

5. Задаются статической характеристикой 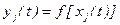в виде линейной зависимости

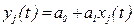. (4.4)

При существующем разбросе значений 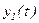коэффициенты

определяют из системы линейных уравнений (метод наименьших квадратов):

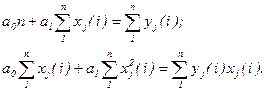(4.5)

Активный метод исследования применяют в тех случаях, когда уровень помех и флуктуаций входных и выходных координат невысок [3].

Пример.

Пусть получен массив данных в виде следующей таблицы соответствий из трех столбцов

xj	xj(1)	xj(2)	xj(3)
yj	yj(1)	yj(2)	yj(3)

Пусть j=1, а конкретные значения в таблице следующие

x1
y1

Допустим, что статическая характеристика аппроксимируется линейной зависимостью (4.4).

Тогда, применив эту зависимость к каждому столбцу таблицы, получим систему из трех уравнений

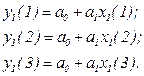
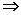
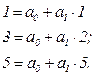(4.6)

Просуммируем левые и правые части уравнений и получим (первое уравнение из (4.5))

.

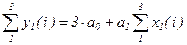
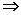
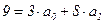Перемножим левую и правую часть каждого уравнения i на значения соответствующей переменной 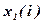и получим:

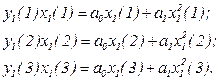
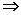
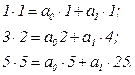(4.7)

Просуммируем левые и правые части уравнений полученной системы и получим (второе уравнение из (4.5))

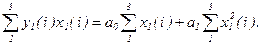
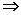
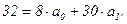
Перепишем полученную систему уравнений

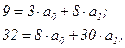
из которой находим коэффициенты статической характеристики .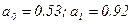

На рисунке 4.2 для сравнения представлены зависимости

:

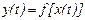исходная и полученная по аппроксимирующему выражению при определенных приведенным способом коэффициентах аппроксимации.

Пассивный метод.

Пассивный метод исследования статических зависимостей сводится к следующему.

1. Производится регистрация случайных изменений входных координат x₁(t), x₂(t),…, x_n(t), имеющих место в режиме нормальной эксплуатации объекта, и соответствующих им флуктуаций выходной координаты y₁(t).

2. Случайные процессы x₁(t), x₂(t),…, x_n(t), y₁(t) квантуются во времени и составляется таблица их значений

x₁(i), x₂(i),…, x_n(i), y₁(i); i=1, 2, …, n.

Примерный вид такой таблицы приведен в таблице 4.1.

Таблица 4.1. К определению статических характеристик

x1(i)	x2(i)	…	y1(i)
x1(1)	x2(1)	…	y1(1)
x1(2)	x2(2)	…	y1(2)
…	…	…	…
x1(n)	x2(n)	…	y1(n)

3. Составляется линейная статическая зависимость

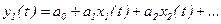
4. Коэффициенты 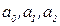определяют из системы линейных алгебраических уравнений (метод наименьших квадратов):

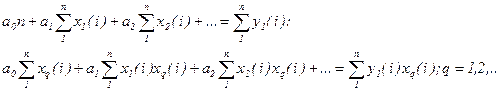
Заметим, что по рассматриваемому методу для составления таблицы необязательна постановка специальных опытов, часто можно использовать показания функционирования приборов.

Уравнения динамики однозначно характеризуют поведение 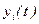во времени при изменении 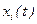и представляют собой дифференциальные или интегральные соотношения.

Изложенное в этом подразделе материал иллюстрирует методический подход к определению характеристик объектов.

В настоящее время существует множество прикладных программ (в том числе в составе EXCEL) для аппроксимации зависимостей в виде полиномов различного порядка – первого (дают линейные зависимости), второго и т.д.

4.2.2. Определение динамических характеристик объектов с помощью периодических воздействий

Динамические свойства объекта с сосредоточенными параметрами однозначно описываются амплитудно-фазовой характеристикой 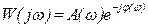, где 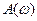- АЧХ, 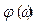- ФЧХ объекта.

Определение АФХ объектов производится чаще всего экспериментально. Суть такого определения сводится к следующему.

Искусственным путем возбуждаются гармонические или иные периодические колебания входной координаты x(t) и с частотой w и регистрируются установившиеся колебания y(t).

Опыты проводятся при и различных частотах w .

Для нахождения АЧХ 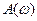требуется измерить амплитуды x(t) и y(t), а для вычисления ФЧХ 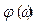- временные сдвиги между гармониками входа и выхода DT.

Схема снятия АФХ с использованием автоматического регулятора

Схема для снятия амплитудно-фазовых характеристик объекта представлена на рисунке 4.3.

Применение синусоидальных воздействий упрощает обработку результатов эксперимента.

Обработка результатов эксперимента по снятию АФХ

Обработку экспериментов по снятию АФХ производят в следующей последовательности (рисунок 4.4):

1) Выбирается несколько периодов установившихся колебаний и провести средние линии входного выходного сигналов 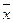и .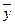

2) Определяются удвоенные амплитуды входного и выходного сигналов и вычислить АФХ для данной частоты 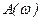по зависимости:

.

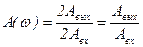Подобные измерения производятся для нескольких периодов (3-5) и определяется среднее арифметическое значение .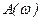

3) Находится фазовый сдвиг выходного сигнала относительно входного. Для этого определяется отрезок 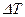между моментами пересечения 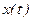и 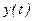средних значени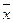й и 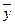при одном номере периода.

Значения 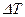усредняются по множеству измерений и вычисляются ФЧХ на частоте :

.

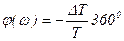Знак “-“ означает отставание выходных колебаний относительно входных.

Повторяют действия для других .

4) Строится график А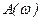ЧХ и ФЧХ .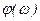

Обработка сильно искаженных помехами гармонических колебаний

Пусть выходной сигнал имеет вид (см. рисунок 4.5)

,

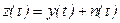где 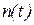- помеха как случайный процесс.

В этих случаях применяют метод статистической обработки результатов эксперимента.

Схема определения АФХ по данному методу (иногда называемому амплитудным) представлена на рисунке 4.6.

На входе объекта задается сигнал

.

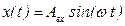На выходе имеем

.

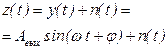Далее вычисляются оценки взаимных корреляционных функций между x(t) и z(t)при нулевом сдвиге

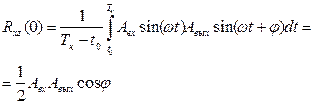(4.7)

и между 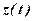и некоторой дополнительной функцией

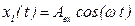
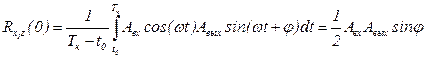, (4.8)

где 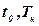- начало и конец интервала наблюдения выходного сигнала.

Из (4.7) и (4.8) находятся АФХ по следующим зависимостям:

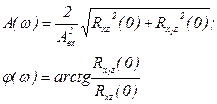. (4.9)

Вся трудность применения этого метода заключается в том, что для определения 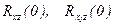необходимо, как следует из рисунка 4.6, вычислительное устройство.

Применение ЛАЧХ для аппроксимации экспериментальных АФХ

Существует много способов определения аналитических выражений коэффициентов АФХ объекта 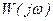. Они громоздки и мало наглядны.

В общем случае динамические свойства объекта можно описать АФХ следующего вида

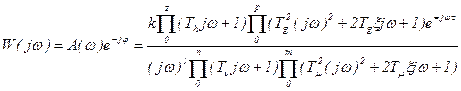. (4.10)

Из этого выражения можно получить ЛАЧФХ:

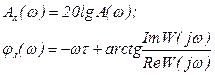. (4.11)

Используя простые кусочно-линейные зависимости ЛАЧХ от частоты, можно провести приближенную аппроксимацию экспериментальной АЧХ набором аналитических выражений:

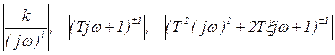. (4.12)

ЛФЧХ используется для определения структуры передаточной функции (определяются величина τ, кратность нулевых полюсов, иногда – порядок знаменателя и т.д.) и проверки правильности аппроксимации всей АФХ.

Этот метод определения передаточной функции по экспериментальным данным связан с графическими построениями и позволяет лишь приближено аппроксимировать экспериментальную АФХ. Поэтому необходимо использовать и комбинированный способ, когда эффективным является и априорный выбор структуры передаточных функций.

4.4.1. Временные характеристики и их свойства

При исследовании поведения САУ во времени достаточно очевидно, что все воздействия имеют случайный, непредсказуемый характер. Следовательно, при анализе и синтезе необходимо сформировать систему типовых воздействий и реакций на них САУ, наиболее достоверно отражающую качество процессов управления. При этом принято считать, что, если САУ хорошо реагирует на некоторое типовое воздействие, а, значит, имеет хорошую типовую динамическую характеристику, то и при произвольных входных воздействиях она будет справляться с задачами управления.

Временная характеристика - это зависимость изменения той или иной величины САУ от времени, возникающего под действием тех или иных факторов. Из временных характеристик в ТАУ наибольшее распространение получили переходная функция и импульсная переходная функция (функция веса, весовая функция).

Схема формирования переходной функции отображена на рисунке 4.7. Переходная функция САУ (объекта, блока, элемента, звена) - это реакция на единичное ступенчатое воздействие. Обычно переходную функцию обозначают символом .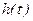

Для снятия переходных характеристик элементов с малой постоянной времени используются быстро действующие измерительные приборы с электрическим сигналом на выходе.

Запись измеряемых сигналов осуществляется с помощью шлейфовых осциллографов или цифровых накопителей.

Переходные характеристики элементов с большой постоянной времени регистрируются обычными многоточечными приборами (потенциометрами).

Один из способов получения динамических характеристик (передаточной функции) связан с проведением экспериментов и с последующей идентификацией свойств объекта.

Условно данная задача может быть представлена в виде рисунка слева. На входе объекта задан известный сигнал u(t). На выходе регистрируется сигнал y(t).

Требуется определить передаточную функцию объекта.

Передаточная функция объекта численно равна отношению преобразования Лапласа его выходной величины и преобразования Лапласа входного воздействия при нулевых начальных условиях.

4.4.2. Определение характеристик апериодического звена

Схема апериодического звена и его реакция на единичный скачок на входе представлены на рисунке 4.8, где W(s) – передаточная функция звена, T – постоянная времени, k – коэффициент передачи.

Как следует из рисунка, график переходной характеристики звена асимптотически стремится к установившемуся уровню k.

При этом плавный характер, отсутствие колебаний и обусловили название “апериодическое” (т.е. непериодическое).

Другое название “инерционное” связано с тем, что постоянная времени T препятствует мгновенному достижению уровня k.

Таким образом, чем больше величина постоянной времени T, тем звено “инерционнее”.

Аналитическое выражение для переходной характеристики звена определяется функцией времени

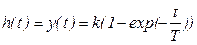(4.13)

Отсюда следует, что при t = T соблюдаются условие 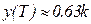, а при - .

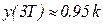4.4.3. Определение характеристик колебательного звена

Как известно, колебательное звено может быть выражено передаточной функцией вида

,

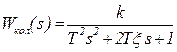где 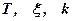- соответственно постоянная времени, коэффициент демпфирования колебаний и k – коэффициент передачи.

Схема колебательного звена и его реакция на единичный скачок на входе представлены на рисунке 4.9. Переходная функция колебательного звена имеет вид [7]

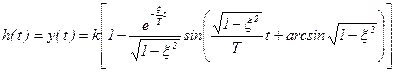. (4.14)

Используя выражение (4.14) можно определить параметры 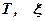колебательного звена. Они находятся из следующих соотношений:

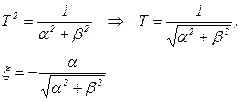(4.15)

Входящие в эти выражения параметры 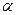и 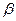вычисляются непосредственно по переходной характеристике следующим образом:

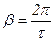- круговая частота, 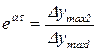- степень затухания (4.16)

где τ - период колебаний;

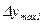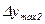, - амплитуды колебаний относительно установившегося значения, отстоящие друг от друга на период колебаний τ.

Из последнего выражения (4.16) имеем:

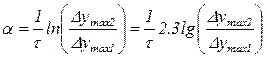. (4.17)

Таким образом, по экспериментально снятой переходной характеристике (подобной представленной на рисунке 4.9) можно найти все параметры колебательного звена, входящие в выражение передаточной функции звена.