Определение удельного заряда электрона методом магнитной фокусировки

ЭЛЕКТРОННОГО ПУЧКА

Физическое обоснование эксперимента

Удельным зарядом электрона называется отношение заряда этой частицы к ее массе . Знание этого отношения является существенным во многих физических явлениях. Так, например, по известным значениям величины заряда и удельного заряда можно вычислить массу частицы. Заряд частицы может быть определен весьма точно. Заряд же любого иона кратен заряду электрона. Кроме того, удельный заряд электрона является одним из параметров, характеризующих движение заряженных частиц в электромагнитных полях.

Существует несколько различных способов определения удельного заряда электрона. Один из них – это метод фокусировки в продольном магнитном поле. Предлагаемый в данной работе метод определения величины важен еще и тем, что позволяет уяснить физическую сущность магнитной фокусировки электронных пучков.

Действие магнитного поля на движущийся заряд

На электрический заряд, движущийся в магнитном поле, действует сила Лоренца

, (38.1)

где q – величина заряда, 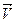– скорость заряда, – индукция магнитного поля.

Эта сила, определяемая как векторное произведение двух векторов, перпендикулярна как к магнитному полю, так и к направлению движения электрического заряда. Если движется отрицательный заряд (электрон), то сила Лоренца направлена в противоположную сторону (рис. 38.1).

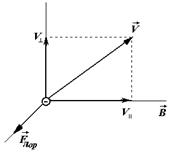
Рис. 38.1 Пространственное соотношение величин магнитной индукции, вектора скорости и силы Лоренца для электрона.

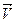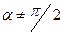Отсюда следует, что если вектор скорости движения заряда составляет с вектором индукции некоторый угол , то вектор скорости можно разложить на две составляющие: продольную 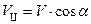и поперечную . При этом значение величины силы Лоренца определяется только поперечной составляющей параметра скорости (е – величина заряда электрона)

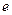
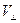
= = . (38.2)

Заряженная частица, движущаяся в однородном магнитном поле перпендикулярно линиям магнитной индукции под действием силы Лоренца, всегда направленной перпендикулярно вектору скорости, приобретает нормальное ускорение и начинает описывать окружность радиусом 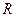в плоскости, перпендикулярной направлению поля. Сила Лоренца в этом случае является центростремительной силой

. (38.3)

В самом общем случае, когда вектор скорости 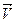движущейся в магнитном поле частицы направлен под углом 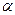к вектору индукции , движение частицы можно представить как наложение двух движений: перемещения вдоль направления магнитного поля и равномерного движения по окружности. В направлении вдоль поля никакие силы на движущуюся частицу не действуют, и она будет двигаться поступательно со скоростью 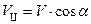. В результате наложения в пространстве поступательного движения и движения по кругу траектория частицы представляет собой винтовую линию (рис.38.2).

Рис. 38.2 Винтовая траектория движения заряженной частицы в магнитном поле

Расстояние, на которое перемещается заряженная частица вдоль поля за один оборот, называется шагом этой линии и определяется из соотношения

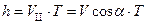, (38.4)

где 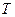– период обращения.

Период обращения – это время, в течение которого частица совершает полный оборот по окружности

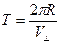. (38.5)

Радиус траектории движения частицы в плоскости, перпендикулярной направлению поля определяется из уравнений (38.2) и (38.3).

Таким образом, для электрона, движущегося в магнитном поле

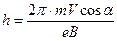. (38.6)

Рассмотрим важный для практики случай, когда угол 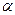невелик и 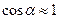. В этом случае путь 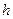, пройденный электроном в магнитном поле за один оборот, практически не зависит от угла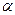

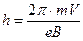. (38.7)

Из этого следует, что все электроны, вышедшие из одной точки под небольшими, но разными углами к магнитному полю, сделав один оборот, вновь соберутся в одной точке. В этом и заключается принцип магнитной фокусировки электронов.

Определение удельного заряда электрона

Метод магнитной фокусировки может быть применен для определения удельного заряда электрона. Впервые этот эксперимент был проведен Бушем и носит его имя.

Установка представляет собой электронно-лучевую трубку, которая помещается внутрь длинного соленоида, создающего достаточно однородное магнитное поле с индукцией . В опытах Буша электроны, испущенные раскаленным катодом, ускоряются, проходя разность потенциалов 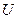, приложенную между катодом и анодом. В результате они приобретают скорость, значение которой может быть найдено из соотношения

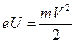(38.8)

Совместное решение уравнений (38.7) и (38.8) дает нам значение удельного заряда электрона, определяемое по формуле

. (38.9)

Параметры анодного потенциала 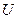и значение индукции магнитного поля определяются экспериментально. Значение величины 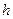является параметром электронно-лучевой трубки, используемой в работе, носит название «постоянная осциллографической трубки» и указывается на приборе.

Описание экспериментальной установки

Для получения пучка электронов с определенной кинетической энергией и фокусировки электронного луча в работе используется стандартная электронно-лучевая трубка (рис. 38.3) с малым диаметром экрана.

Рис. 38.3 Общий вид электронно-лучевой трубки.

Электроны, испускаемые подогретым катодом, проходят сквозь управляющую сетку (первый управляющий электрод или модулятор) и два ускоряющих анода. Для фокусировки электронного пучка на управляющий электрод подается отрицательный потенциал. Поле этого электрода сжимает электронный пучок, выходящий из катода. На ускоряющие аноды подаются положительные потенциалы, изменением которых достигается фокусировка электронного пучка на экране и яркость свечения. Сфокусированный электронный пучок проходит далее систему вертикально и горизонтально отклоняющих электродов (управляющие пластины), на которые подается переменное напряжение. Управляющие пластины позволяют перемещать электронный пучок на экране в произвольном направлении. Принципиальная электрическая схема установки приведена на рис.38.4.

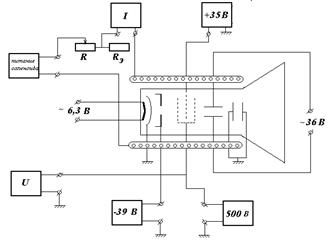
Рис. 38.4 Электрическая блок-схема установки.

Напряжение на электроды трубки подается от источников высокого напряжения типа У-1136 и блока питания Б3-2. Напряжение накала катода ~ 6,3 В. Отрицательное напряжение, подаваемое на модулятор, составляет величину -39 В. На первый анод электронно-лучевой трубки подается напряжение +35 В. Напряжение, подаваемое на второй анод, регулируется в диапазоне от 500 до 800 вольт и измеряется с помощью электронного вольтметра ВК 7-10А/1. На вертикально отклоняющие пластины подается переменное напряжение порядка 36 В от понижающего трансформатора. Горизонтальные пластины заземлены и соединены с катодом.

Электронно-лучевая трубка располагается по оси соленоида, внутри которого постоянным током, проходящим по катушке соленоида, создается осевое магнитное поле. Катушка соленоида питается от стабилизированного источника напряжения ВС-25, при этом величина протекающего по катушке тока регулируется реостатом 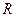. Для точного измерения тока соленоида применяется эталонное сопротивление 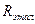, падение напряжение на котором измеряется электронным вольтамперметром ВК2-20.

Порядок выполнения работы

Учитывая тот факт, что магнитное поле на оси соленоида определяется следующим выражением

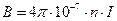, (38.10)

где – индукция магнитного поля в теслах, – число витков катушки на единицу длины, 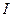– ток в амперах, рабочую формулу (38.9) для расчета величины удельного заряда электрона можно преобразовать к виду

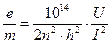, (38.11)

где характеристические параметры установки и 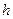– постоянные величины, соответственно равные = 2393 витка на 1 метр, 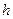= 0,00253 м; параметры напряжения 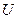на втором аноде и значение величины тока катушки соленоида 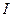измеряются в процессе эксперимента.

На втором аноде трубки устанавливают несколько значений анодного потенциала с шагом 20 В. При данном анодном напряжении ток катушки соленоида устанавливают таким, чтобы луч электронной трубки на экране фокусировался бы в одно маленькое пятно. После этого измеряют падение напряжения на эталонном сопротивлении 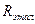и по закону Ома рассчитывают ток соленоида 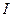. Фокусировка луча при заданном анодном потенциале производится не менее пяти раз, при этом каждый раз определяют ток соленоида. Для каждой фокусировки определяют отношение 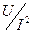, затем определяют среднее значение и среднеквадратичную погрешность этой величины.

Содержание отчета

1. Электрическая схема установки.

2. Среднее значений отношений 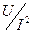для выбранных анодных напряжений и окончательный расчет по алгоритму прямых измерений доверительной границы этого значения.

3. Окончательное значение величины удельного заряда электрона с указанием его доверительной границы.

Контрольные вопросы

s Как движется электрон в электронно-лучевой трубке при наличии магнитного поля?

s Почему электрон движется равномерно, хотя на аноде имеется анодное напряжение?

s Почему по окружности электрон движется равномерно, несмотря на то, что существует центростремительное ускорение?

Лабораторная работа 39