Гармонические колебания. Комплексные токи и напряжения

СВОЙСТВА И МЕТОДЫ РАСЧЕТА ЛИНЕЙНЫХ ЦЕПЕЙ

С ИСТОЧНИКАМИ ГАРМОНИЧЕСКОГО ТОКА (37с.)

Гармонические колебания. Комплексные токи и напряжения

Гармоническими называются сигналы, ток и напряжение которых изменяются во времени по закону косинуса (или синуса) :

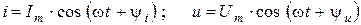, (2. 1)

где 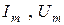— амплитуды тока и напряжения,

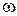— угловая частота,

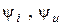— начальные фазы тока и напряжения.

Угловая частота 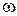определяется через период и частоту колебаний

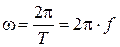рад/с

где 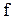— частота (Гц) .

В установившемся режиме начальная фаза гармонических колебаний не играет роли и выбирается из соображений удобства. Если рассматриваются одновременно несколько колебаний, то имеет значение разность их начальных фаз (сдвиг фаз). На рисунке 2. 1 показаны гармонические колебания тока и напряжения в некотором участке цепи, описываемые формулами (2. 1) .

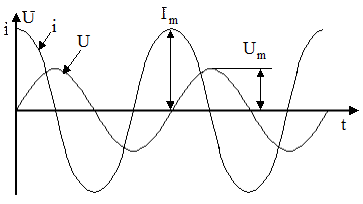
Рисунок 2. 1

Начальная фаза тока принята равной нулю, а начальная фаза напряжения равна — :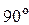

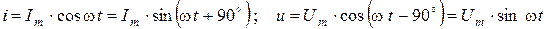
Угол сдвига фаз напряжения и тока 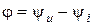в данном случае равен 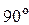. Это значит, что напряжение отстает по фазе от тока на .

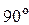Часто пользуются понятием “действующее значение” периодического тока. Под действующим значением тока понимают такой постоянный ток, который в одном и том же сопротивлении за один период выделяет такое же количество тепла, как и периодический ток. Этому определению соответствует равенство

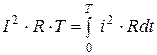, (2. 2)

где i — мгновенное значение периодического тока,

I — действующее значение.

Из выражения (2. 2) находим

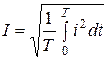. (2. 3)

В частности, для гармонического тока, подставляя его формулу из (2. 1) в соотношение (2. 3), получим

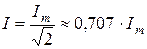. (2. 4)

Аналогично можно ввести понятие и величину действующего значения гармонического напряжения

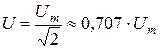. (2. 5)

В радиоэлектронике обычно приходится иметь дело с амплитудными значениями токов и напряжений. Но в ряде случаев, например, при проектировании источников питания, расчеты ведут, используя действующие значения, как это принято в электроэнергетике.

Если в линейных электрических цепях действуют гармонические источники, то в установившемся режиме токи и напряжения во всех участках цепи будут также гармоническими. В общем случае линейная цепь гармонического тока может содержать резисторы, катушки индуктивности, конденсаторы, некоторые участки могут быть магнитно-связанными (взаимная индуктивность). Расчет цепи может заключаться в определении токов ветвей, напряжений на отдельных участках, а также в отыскании характеристических функций цепи (коэффициентов передачи, входного сопротивления и т. д.). Очевидно, что оперировать с токами и напряжениями в гармонической форме при составлении и решении уравнений по законам Кирхгофа крайне неудобно, отношения токов и напряжений (сопротивления, коэффициенты передачи и т. д.) и вовсе не имеют смысла, так как они изменяются во времени. Поэтому анализ электрических цепей при гармонических воздействиях ведется на основе так называемого символического, или комплексного метода, согласно которому гармонические функции времени (ток, напряжение и др. ) представляются векторами или комплексными числами.

Пусть ток изменится по гармоническому закону. Рассмотрим комплексную плоскость, заданную ортами 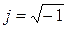— мнимая ось и +1 — вещественная ось. Поместим на плоскости вектор 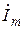длиной 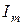под углом 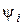к вещественной оси и приведем его во вращение вокруг начала координат с угловой скоростью 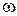(рисунок 2. 2) .

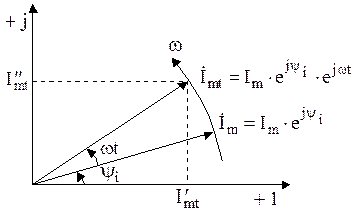
Рисунок 2. 2

По истечении времени t вектор займет положение. Угол, на который он повернется относительно вещественной оси, будет равен 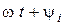. Его проекция 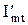и 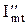на вещественную и мнимую оси будут соответственно равны

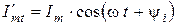и .

Таким образом, проекция вектора 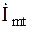на вещественную ось является исходной гармонической функцией. Вектор 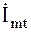можно записать и как комплексное число через его проекции

.

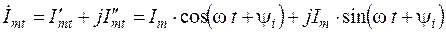Используя формулу Эйлера 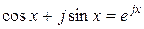, последнее выражение можно переписать в виде

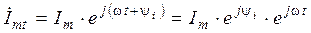(2. 6)

Эта формула является комплексным изображением тока в любой момент времени. Однако в большинстве случаев достаточно знать положение вектора в начальный момент времени t = 0 . Тогда выражение (2. 6) приобретает вид

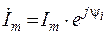. (2. 7)

Это комплексное число (вектор) , модуль которого равен амплитуде тока 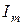, а угол- начальной фазе 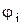, называется комплексной амплитудой тока или комплексным током.

По аналогии можно ввести понятия и величины : комплексное напряжение 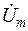, комплексная ЭДС 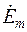, комплексный магнитный поток 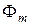и т. д.

С помощью комплексного метода расчет цепей при гармонических воздействиях существенно упрощается.

Пример . Найти напряжение, приложенное ко входу цепи на рисунке 2. 3,

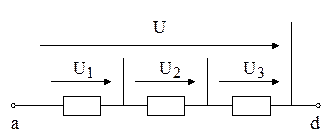
Рисунок 2. 3

если напряжение на элементах изменяется по гармоническим законам

.

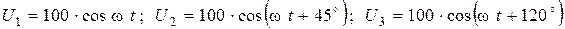Для наглядности изобразим эти напряжения в виде векторов (векторная диаграмма, рисунок 2. 4) .

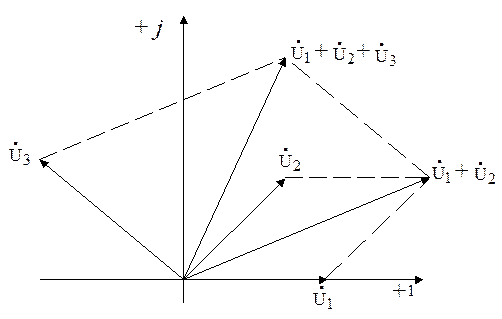
Рисунок 2. 4

При вращении векторов их взаимное положение не будет изменяться. Поэтому достаточно указать их начальные положения. Согласно второму закону Кирхгофа

.

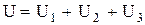Сложение мгновенных значений можно заменить сложением векторов или комплексных чисел, изображающих эти напряжения. Такая замена основана на том, что проекция суммы векторов равна сумме проекций. В аналитической форме общее комплексное напряжение находится следующим образом

.

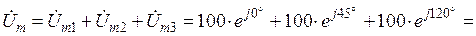
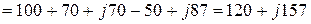Амплитуда общего напряжения 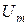находится как модуль :

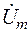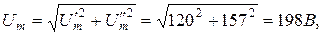
а начальная фаза с помощью соотношения

.

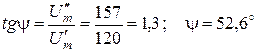Аналогично можно находить и сумму гармонических токов. Вместо комплексных амплитуд напряжений и токов при анализе можно использовать комплексное действующее значение

.
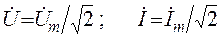