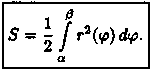Теорема о среднем для определённого интеграла.
Если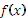 
-неотрицательная функция на промежутке 
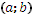и ограничена на нём, то 
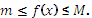Проинтегрируем:
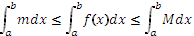
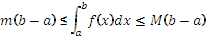; разделим все на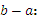 
.
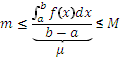
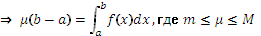Следствие: если 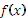- непрерывна на отрезке 
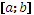, то она принимает все значения от 
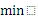до 
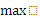, в том числе и 
.
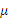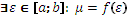
19. Критерий интегрируемости ограниченной на отрезке функции.
Критерии интегрируемости.
Необходимое условие: функция f должна быть ограниченной на отрезке [a,b].
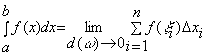
Критерий Коши:
Для существования неопределенного интеграла необходимо и достаточно, чтобы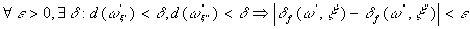 
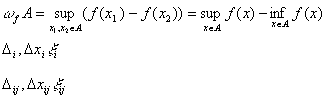
Достаточный признак:
Для интегрирования f достаточно.
.
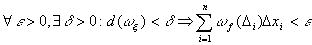Доказательство:
В отрезке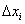 
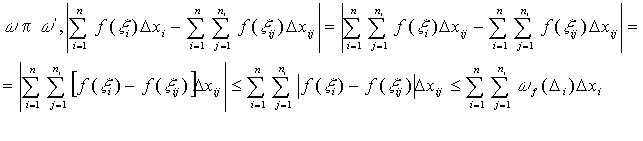Пусть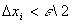 
, тогда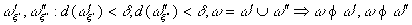 
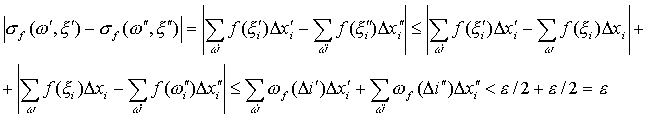
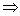
f интегрируемая функция, ч.т.д.
Следствие №1
Если функция f ограничена на [a, b] и имеем на нем конечное число точек разрыва, то функция fинтегрируема на [a, b].
Доказательство:
Пусть f имеет на [a, b] k-точек разрыва
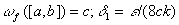
Рассмотрим у каждой точки разрыва с радиусом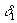 
и вычтем из отрезка
+ 
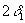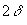
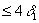
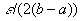выберем 
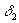, такое, что 
; 
; 
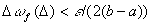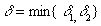
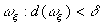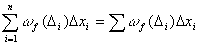{берётся по отрезкам, которые не пересекаются с окрестностью точек разрыва}+ 
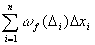{все остальные}
< 
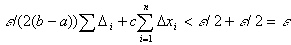ч.т.д.
20. Теорема об интегрируемости непрерывной на отрезке функции.
Следствие №2
Если функция f непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Доказательство:
f - непрерывна на [a, b] 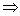она равномерно непрерывна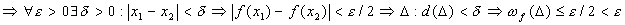 
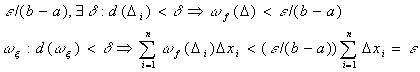ч.т.д.
21. Теорема об интегрируемости монотонной на отрезке функции.
Следствие №3
Если f(x) ограничена и монотонна на [a, b], то она интегрируема на этом отрезке.
Доказательство:
; 
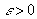
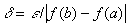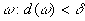
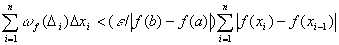
в силу монотонности функции все разности под знаком модуля в получившейся сумме имеют один знак
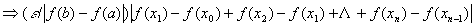{т.к. 
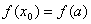и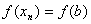 
}= 
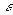ч.т.д.
22. Интеграл с переменным верхним пределом. Производная интеграла с переменным верхним пределом.
________
23. Формула Ньютона-Лейбница.
_________
Геометрические приложения определённого интеграла: площади плоских фигур, длина кривых. Вычисление объёма тел, в том числе тел вращения.
Вычисление площадей плоских фигур
Прямоугольные координаты
Площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному интегралу:
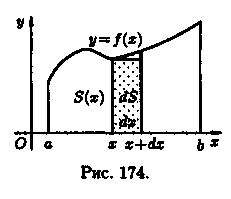
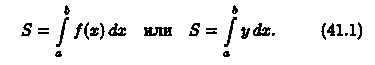
Формула (41.1) получена путем применения метода сумм. Пусть криволинейная трапеция ограничена линиями у = ƒ(х) ≥ 0, х = а, х = b, у = 0 (см. рис. 174).
Для нахождения площади S этой трапеции проделаем следующие операции:
1. Возьмем произвольное х [а; b] и будем считать, что S = S(x).
2. Дадим аргументу х приращение Δх = dx (х + Δх є [а; b]). Функция S = S(x) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).
Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у • dx.
3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем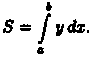 
Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь может быть найдена по формуле
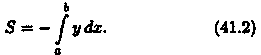
Формулы (41.1)и (41.2) можно объединить в одну:
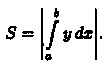
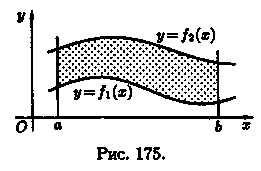
Если криволинейная трапеция ограничена прямыми у = с и у=d, осью Оу и непрерывной кривой х = φ(у) ≥ 0 (см. рис. 177), то ее площадь находится по формуле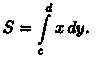 
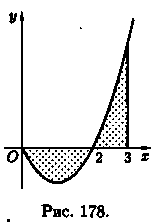И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически
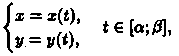
прямыми х = а и х = b и осью Ох, то площадь ее находится по формуле
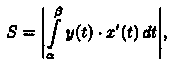
где а и β определяются из равенств х(а) = а и х(β) =b.
Полярные координаты
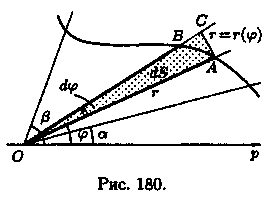
Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ — полярные координаты (см. рис. 180).
1. Будем считать часть искомой площади S как функцию угла φ, т. е. S = S(φ), где а ≤φ≤β (если φ = а, то S(a) = 0, если φ=β, то S(β) = S).
2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.
Дифференциал dS представляет собой главную часть приращения ΔS при dφ→0 и равен площади кругового сектора О АС (на рисунке она заштрихована) радиуса r с центральным углом dφ. Поэтому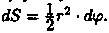 
3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь
