Правило дифференцирования сложной функции
Следующая теорема даёт правило дифференцирования сложной функции.
Теорема 6.2.Если функция х = φ(t) имеет производную в точке t0, а функция у = f(x) имеет производную в соответствующей точке х0 = φ(t0), то сложная функция f(φ(t)) имеет производную в точке t0, причём имеет место следующая формула
у'(t0) = f '(x0) × φ'(t0).
Пример 6.4.Вычислить у', если у = 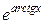 .
.
Решение. Данную функцию можно представить в виде у = 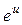 , где
, где 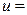
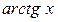 . Тогда по теореме 6.2 у'(
. Тогда по теореме 6.2 у'( 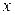 ) = у'(
) = у'( 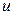 ) ×
) × 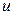 '(
'( 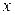 ) = (
) = ( 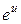 )' × (
)' × ( 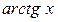 )' = =
)' = = 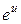 ×
× 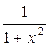 =
= 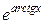 ×
× 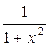 .
.
Замечание 6.1. В теореме 6.2 мы рассмотрели сложную функцию, где у зависит от переменной t через одну промежуточную переменную х. Возможна и более сложная зависимость – с несколькими промежуточными переменными. При этом правило дифференцирования остаётся прежним.
Пример 6.5.Вычислить производную функцию у = tg2( 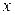 2+1).
2+1).
Решение. Данную функцию можно представить в виде у = 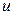 2,
2, 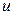 = tg
= tg 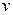 ,
, 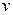 =
= 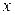 2+1. Тогда
2+1. Тогда
у'( 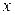 ) = у '(
) = у '( 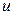 ) ×
) × 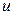 '(
'( 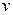 ) ×
) × 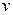 '(
'( 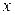 ) = (
) = ( 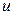 2)' × (tg
2)' × (tg 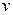 )' × (
)' × ( 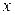 2+1)' = =
2+1)' = = 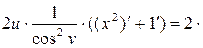 tg
tg 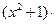
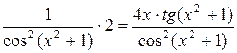 .
.
Мы уже отмечали, что производная f '(х) функции у = f(x) сама является функцией аргумента х. Следовательно, по отношению к ней снова можно ставить вопрос о существовании и нахождении производной.
6.4 Производная n-го порядка
Определение 6.4.Назовём f '(х) производной первого порядкафункции у = f(x), дифференцируемой на некотором промежутке ( 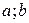 ). Производная от f '(х) называется производной второго порядкафункции у = f(x) и обозначается f ''(x). Производная от f ''(x) называется производной третьего порядка, обозначается f '''(x). Таким образом определяется производная n-го порядка для любого натурального n. Производные, начиная со второй, называются производными высшего порядка и обозначаются: у'', у''', у(4), у(5),…, у(n),… . Итак, по определению
). Производная от f '(х) называется производной второго порядкафункции у = f(x) и обозначается f ''(x). Производная от f ''(x) называется производной третьего порядка, обозначается f '''(x). Таким образом определяется производная n-го порядка для любого натурального n. Производные, начиная со второй, называются производными высшего порядка и обозначаются: у'', у''', у(4), у(5),…, у(n),… . Итак, по определению
у(n) = (у(n – 1))' , n = 2, 3, … .
Пример 6.6.Вычислить производную третьего порядка функции у = 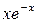 .
.
Решение.1) у' = 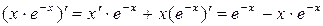 ;
;
2) у'' = (у')' = 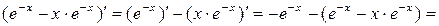
= 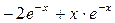 ;
;
3) у''' = (у'')' = ( 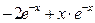 )' =
)' = 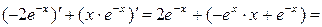 =
= 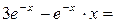
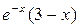 .
.
Определение 6.5.Пусть функция у = f (x) дифференцируема в каждой точке некоторого промежутка. Дифференциал dy = f '(x)dx называется дифференциалом первого порядкафункции у = f(x). Дифференциалы высших порядков(второго, третьего и т. д.) определяются следующей формулой
dny = f (n)(x)(dx)n, n = 2, 3,… .
Пример 6.7.Вычислить дифференциал d2y, где у = х4 − 3х2 + 4.
Решение.1) dy = (х4 − 3х2 + 4)'dx = (4х3 – 6х)dx;
2) d2y = (4x3 – 6x)'(dx) = (12x2 – 6)(dx)2.
Вопросы для самоконтроля
1. Сформулируйте определение производной.
2. Каков геометрический смысл производной?
3. Какая функция называется дифференцированной в точке?
4. Что называют дифференциалом функции?
5. Сформулируйте основные правила дифференцирования функции.
6. По какому правилу находится дифференцирование сложной функции?
7. Как находятся производные и дифференциал высших порядков?
Основные теоремы дифференциального исчисления
Основные теоремы дифференциального исчисления
Теорема Ферма
Теорема 7.1.Пусть функция f(x) определена ( 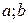 ) и в некоторой точке х0 этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке х0 существует производная, то она равна нулю, т. е. f ¢(x) = 0.
) и в некоторой точке х0 этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке х0 существует производная, то она равна нулю, т. е. f ¢(x) = 0.
Доказательство.Пусть для определённости в точке х0 функция f (x) имеет наибольшее значение, т. е. для любого х Î ( 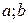 ) выполняется неравенство f (x) £ f (x0). Это означает, что ∆у = f (x0 + ∆x) – f (x0) £ 0 для любого приращения аргумента ∆х. Возможны два случая:
) выполняется неравенство f (x) £ f (x0). Это означает, что ∆у = f (x0 + ∆x) – f (x0) £ 0 для любого приращения аргумента ∆х. Возможны два случая:
1) ∆х > 0. Тогда 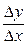 £ 0 и, следовательно,
£ 0 и, следовательно,
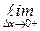
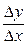 =
= 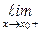
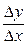 £ 0;
£ 0;
2) ∆х < 0. Тогда 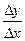 ³ 0 и, следовательно,
³ 0 и, следовательно,
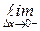
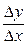 =
= 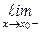
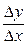 ³ 0.
³ 0.
По условию, f ¢(x) существует, поэтому существует 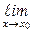
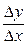 . Но тогда существуют односторонние пределы
. Но тогда существуют односторонние пределы 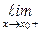
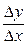 и
и 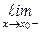
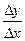 , причём
, причём
0 £ 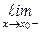
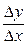 =
= 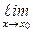
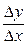 =
= 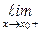
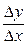 £ 0.
£ 0.
Всё это возможно только при 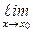
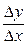 = 0, т. е. при f ¢(x) = 0.
= 0, т. е. при f ¢(x) = 0.
Аналогично рассматривается случай, когда в точке х0 функция f (x) имеет наименьшее значение.
Теорема Ролля
Теорема 7.2.Пусть на [  ] определена функция f (x), причём: 1) f (x) непрерывна на [
] определена функция f (x), причём: 1) f (x) непрерывна на [  ]; 2) f (x) дифференцируема на (
]; 2) f (x) дифференцируема на (  ); 3) f (
); 3) f ( 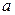 ) = f (
) = f ( 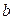 ). Тогда существует точка
). Тогда существует точка 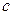 Î(
Î(  ), в которой f ¢(
), в которой f ¢( 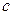 ) = 0.
) = 0.
Доказательство.Так как функция f (x) непрерывна на [  ], то по второй теореме Вейерштрасса она имеет на этом отрезке максимальное значение М и минимальное значение m, т. е. существуют такие точки х1, х2 Î [
], то по второй теореме Вейерштрасса она имеет на этом отрезке максимальное значение М и минимальное значение m, т. е. существуют такие точки х1, х2 Î [  ], в которых f (x1) = m, f (x2) = M и выполняются неравенства
], в которых f (x1) = m, f (x2) = M и выполняются неравенства
m £ f (x) £ M для всех х Î [  ].
].
Возможны два случая:
1) M = m. Тогда f (x) = const = M = m. В этом случае для любого х Î ( 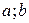 ) имеем f '(x) = 0. Теорема верна;
) имеем f '(x) = 0. Теорема верна;
2) m < M. Так как f ( 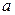 ) = f (
) = f ( 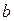 ), то хотя бы одно значение m или М достигается на (
), то хотя бы одно значение m или М достигается на ( 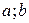 ), т. е. существует
), т. е. существует 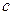 Î (
Î (  ) такая, что f (
) такая, что f ( 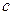 ) = m или f (
) = m или f ( 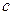 ) = M. Поскольку f (x) дифференцируема в точке
) = M. Поскольку f (x) дифференцируема в точке 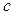 , то по теореме Ферма f '(
, то по теореме Ферма f '( 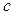 ) = 0.
) = 0.
Теорема Лагранжа
Теорема 7.3.Пусть на отрезке [  ] определена функция f (x), причём 1) f (x) непрерывна на [
] определена функция f (x), причём 1) f (x) непрерывна на [  ]; 2) f (x) дифференцируема на (
]; 2) f (x) дифференцируема на (  ). Тогда существует точка
). Тогда существует точка 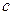 Î (
Î (  ) такая, что справедлива формула
) такая, что справедлива формула
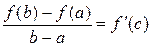 .
.
Доказательство.Введём в рассмотрение на [  ] вспомогательную функцию
] вспомогательную функцию
F(x) = f (x) – f ( 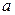 ) −
) − 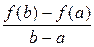 × (x −
× (x − 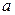 ).
).
Функция F(x) удовлетворяют всем трём условиям теоремы Ролля:
1) F(x) непрерывна на [  ] как разность двух непрерывных функций f (x) и линейной функции
] как разность двух непрерывных функций f (x) и линейной функции
f ( 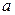 ) +
) + 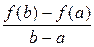 × (x −
× (x − 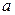 );
);
2) F(x) дифференцируема на (  ). Действительно, f (x) дифференцируема на (
). Действительно, f (x) дифференцируема на (  ) по условию, поэтому производная F '(x) = f '(x) −
) по условию, поэтому производная F '(x) = f '(x) − 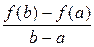 существует на (
существует на (  );
);
3) F( 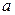 ) = 0; F(
) = 0; F( 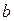 ) = 0, т. е. F(
) = 0, т. е. F( 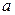 ) = F(
) = F( 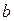 ).
).
Тогда по теореме Ролля существует точка 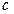 Î (
Î (  ) такая, что F '(
) такая, что F '( 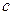 ) = 0, т. е.
) = 0, т. е.
f '( 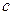 ) =
) = 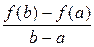 .
.
Равенство f ( 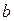 ) – f (
) – f ( 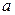 ) = f '(
) = f '( 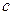 )(
)( 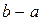 ) называется формулой Лагранжаили формулой конечных приращений.
) называется формулой Лагранжаили формулой конечных приращений.
Теорема Коши
Теорема 7.4.Пусть функции f (x) и g(x) непрерывны на [  ] и дифференцируемы на (
] и дифференцируемы на (  ). Пусть, кроме того, g'(x) ≠ 0. Тогда на (
). Пусть, кроме того, g'(x) ≠ 0. Тогда на (  ) существует точка
) существует точка 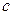 такая, что справедлива формула
такая, что справедлива формула
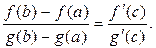 (7.1)
(7.1)
Доказательство.Прежде всего отметим, что g( 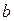 ) ≠ g(
) ≠ g( 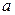 ), т. е. формула (7.1) имеет смысл. Если предположить, что g(
), т. е. формула (7.1) имеет смысл. Если предположить, что g( 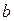 ) = g(
) = g( 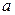 ), то по теореме Ролля для функции g(x) на (
), то по теореме Ролля для функции g(x) на (  ) найдётся точка h такая, что g'(h) = 0. Это противоречит условию g'(x) ≠ 0 на (
) найдётся точка h такая, что g'(h) = 0. Это противоречит условию g'(x) ≠ 0 на (  ).
).
Рассмотрим на [  ] вспомогательную функцию
] вспомогательную функцию
F '(x) = f '(x) − 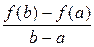 × g'(x), то f '(
× g'(x), то f '( 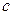 ) −
) − 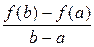 × g'(
× g'( 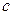 ) = 0,
) = 0,
откуда, учитывая g'( 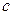 ) ≠ 0, получим
) ≠ 0, получим
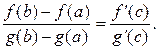
Формула (7.1) называется формулой Кошиили обобщённой формулой конечных приращений.
Замечание 7.1. Если в формуле Коши взять функцию g(x) = x, то получим формулу Лагранжа.
Снова вернёмся к вопросу раскрытия неопределённостей. Познакомимся с простым и эффективным методом раскрытия неопределённостей, который называется правилом Лопиталя–Бернулли. Основано это правило на следующей теореме.
7.2 Правило Лопиталя–Бернулли
Теорема 7.5.Пусть функции f (x) и g(x) определены и дифференцируемы на некотором интервале (  ), содержащем точку х0, за исключением, быть может, самой точки х0. Пусть, далее,
), содержащем точку х0, за исключением, быть может, самой точки х0. Пусть, далее, 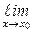 f (x) =
f (x) = 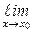 g(x) = 0 и g'(x) ≠ 0 на (
g(x) = 0 и g'(x) ≠ 0 на (  ). Тогда, если существует
). Тогда, если существует 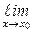
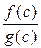 , причём
, причём
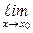
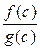 =
= 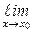
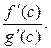
Пример 7.1.Найти 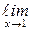
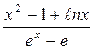 .
.
Решение.Функции f (x) = 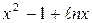 и g(x) =
и g(x) = 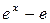 определены и дифференцируемы на (
определены и дифференцируемы на ( 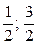 ), причём
), причём 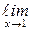 f (x) =
f (x) = 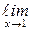 g(x) = 0. Предел отношения производных этих функций существует:
g(x) = 0. Предел отношения производных этих функций существует:
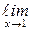
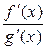 =
= 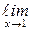
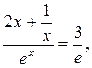
причём g'(x) = 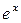 ≠ 0 для х Î (
≠ 0 для х Î ( 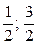 ). Теперь по теореме Лопиталя–Бернулли существует
). Теперь по теореме Лопиталя–Бернулли существует 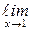
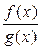 , причём
, причём
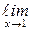
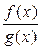 =
= 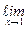
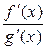 =
= 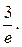
Замечание 7.2.Теорема Лопиталя–Бернулли позволяет раскрывать неопределённости 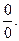
Замечание 7.3.Обычно при вычислении пределов записывают только необходимые преобразования, а проверку выполнения условий теоремы Лопиталя–Бернулли делают по ходу вычислений. Если при этом окажется, что отношение производных снова представляет неопределённость 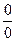 , то правило Лопиталя–Бернулли применяют повторно.
, то правило Лопиталя–Бернулли применяют повторно.
Пример 7.2.
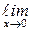
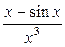 =
= 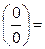
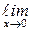
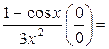
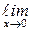
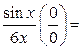
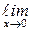
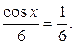
Замечание 7.4.Теорема Лопиталя–Бернулли остаётся верной и в случае, когда х → ∞, х → +∞, х → −∞.
Пример 7.3.
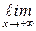
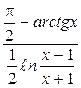
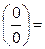
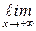
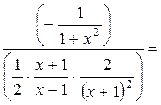
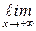
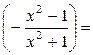 −
− 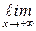
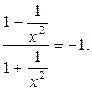
Замечание 7.5. Если в теореме Лопиталя–Бернулли заменить требование
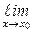 f (x) =
f (x) = 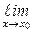 g(x) = 0 на условие
g(x) = 0 на условие 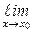 f (x) =
f (x) = 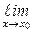 g(x) = ∞,
g(x) = ∞,
то теорема остаётся верной. В такой формулировке правило Лопиталя-Бернулли позволяет раскрывать неопределённости вида 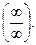
Пример 7.4.Найти 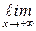
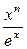 .
.
Решение. 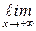
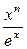
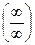 =
= 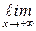
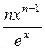
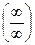 =
= 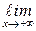
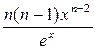 =…=
=…= 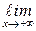
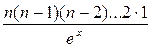 =
=
= 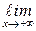
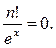
Замечание 7.6.Неопределённости вида 0 × ∞ и ∞ − ∞ можно свести к неопределённостям вида 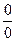 и
и 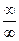 , а затем раскрыть с помощью правила Лопиталя–Бернулли.
, а затем раскрыть с помощью правила Лопиталя–Бернулли.
Пример 7.5.Найти предел 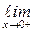
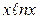 .
.
Решение. 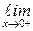 (
( 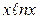 ) = (0 × ∞) =
) = (0 × ∞) = 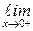
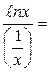
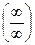 =
= 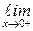
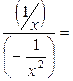
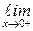
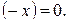
Пример 7.6. 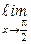
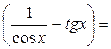 (∞ − ∞)=
(∞ − ∞)= 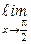
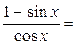
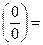
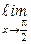
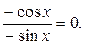
Замечание 7.7.Неопределённости вида 00, 1∞, ∞0 имеют место при рассмотрении функций у = f (x)g(x). Эти неопределённости с помощью тождества
f (x)g(x) = еg(x)ℓnf (x)
сводятся к неопределённостям, которые рассмотрены выше.
Пример 7.7. 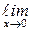
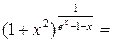 (1∞) =
(1∞) = 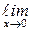
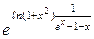 =
= 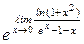 =
= 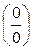 = =
= = 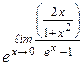 =
= 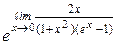 =
= 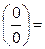
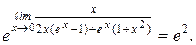
Пример 7.8. 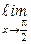
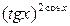 = (∞0) =
= (∞0) = 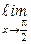
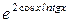 =
= 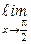
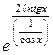 =
= 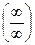 = =
= = 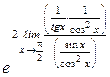 =
= 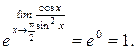
Замечание 7.8.Однако правило Лопиталя–Бернулли не всегда применимо.
Пример 7.9.Найти 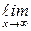
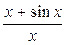 .
.
Решение.Имеем неопределённость вида 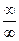 . Однако правило Лопиталя–Бернулли применить здесь нельзя, т. к.
. Однако правило Лопиталя–Бернулли применить здесь нельзя, т. к.
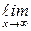
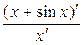 =
= 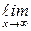
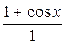 не существует.
не существует.
В таких случаях ищут методы раскрытия неопределённостей без правила Лопиталя–Бернулли.
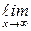
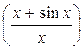 =
= 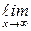
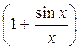 = 1+
= 1+ 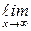
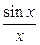 = 1.
= 1.
Вопросы для самоконтроля
1. Сформулируйте основные теоремы дифференциального исчисления.
2. В чем заключается теорема Ферма?
3. Каким условиям должна удовлетворять функция f (x) на отрезке [  ],чтобы для нее была справедлива теорема Ролля?
],чтобы для нее была справедлива теорема Ролля?
4. Сформулируйте теорему Лагранжа.
5. В чем заключается теорема Коши?
6. Какие неопределенности раскрывает правило Лопиталя–Бернулли?
7. Сформулируйте правило Лопиталя–Бернулли.
Исследование функций
