RC - тізбегінің қысқа тұйықталуы
R,L,C элементтерінің тізбектей жалғануы.Векторлық диаграммасы.
 ;
; 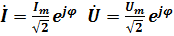
u=uR+uL+uC
u=i*R+L*di/dt+1/cʃidt
U=I*R+I*jXL+I*(-jXc)= I(R+j(Xl-Xc));
RC - тізбегінің қысқа тұйықталуы.
R, C тізбекте қысқа тұйықталу
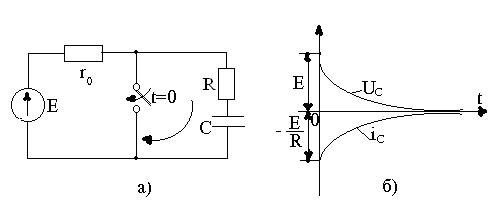
2.7сурет- R, C тізбектің қысқа тұйықталғаны.
а)- есептеу сүлбе;
б)- кернеудің және тоқтың қисықтары.
Тұрақты кернеу көзіне Е жалғанған тізбек  кезде қысқа тұйықталады (2.7, а-сурет). Сол себептен, R және С элементтерден құралған контурда лезде сыйымдылықтағы кернеу жоқ болып кетпейді: электр ағынның энергия есебімен сыйымдылықтағы кернеудің өзгеруі байсалды өтеді (2.7, б сурет). Контурдағы қалыптасқан кернеу және ток нөлге тең болады. (2.1) теңдеуде
кезде қысқа тұйықталады (2.7, а-сурет). Сол себептен, R және С элементтерден құралған контурда лезде сыйымдылықтағы кернеу жоқ болып кетпейді: электр ағынның энергия есебімен сыйымдылықтағы кернеудің өзгеруі байсалды өтеді (2.7, б сурет). Контурдағы қалыптасқан кернеу және ток нөлге тең болады. (2.1) теңдеуде  деп алғанда, шығады
деп алғанда, шығады
 .
.
Конденсатор Е кернеуге дейін қысқа тұйықталу алдында зарядталған. Интегралдаудың тұрақтысын басты жағдайлардан белгілейміз:
 кезде
кезде  .
.
Сонымен, конденсатордағы кернеу 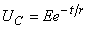 . (2.7)
. (2.7)
Ток  . (2.8)
. (2.8)
R кедергіде өтпелі процесс кезде таратылатын энергия электр өрісте коммутацияға дейін жиналған энергияға тең:
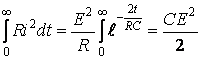 .
.
35. RL - тізбегінің қысқа тұйықталуы.  Тұрақты немесе айнымалы кернеу көзіне қосылып тұрған R, L тізбек t=0 кезде тұйықталып қалады.
Тұрақты немесе айнымалы кернеу көзіне қосылып тұрған R, L тізбек t=0 кезде тұйықталып қалады.
R, L тізбектегі қысқа тұйықталу. a)-есептеу сүлбе; б) і тоқтың және UL кернеудің қисықтары.
Сол себептен құрылған, R және L контурда индуктивтік орауыштың ішінде магнит ағыны болғандықтан ток лезде жоқ болып кетпейді: магнит ағынының азаюымен пайда болатын өздік индукцияның ЭҚК-і контурдағы токты мгнит өрістің энергиясы есебімен қолдайды. Магнит өрістің энергиясы тарап, R кедергіде жылулыққа айналады, ал контурдағы ток 0-ге жақындайды, яғни:ік=0.
ік=0 деп алғанда, шығады:
i=Ae-(R/L)*t=Ae-t/r
Интегралдаудың тұрақтысы басты жағдайдан табылады i(0)=i(-0),
i(t)=i(0)e-t/r=i(0)e(-R/L)*t
Индуктивтегі кернеудің қисығы:
UL=Ldi/dt= -Ri(0)e-t/r
33. Айным1алы кернеу көзіне қосылған RL тізбегіндегі өтпелі кезең.R, L тізбекке синусоидалды ЭҚК е = Emsin(ωt + ψ) қосылғанда қалыптасқан ток болады
іқ =Imsin (ωt + ψ - φ),
мұнда 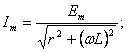
 .
.
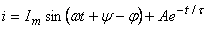 , мұнда
, мұнда 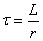 .
.
Интегралдаудың тұрақтысы басты жағдай і(0) = і(0-) = 0 бойынша белгіленеді.
Сондықтан, 0 = Imsin (ψ - φ) + А, ал бұдан А = -Imsin (ψ - φ).
Өтпелі ток тізбекте
 .
.
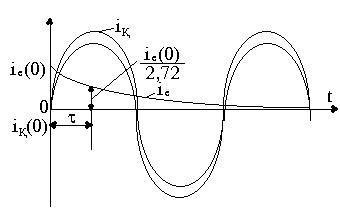 2.4 сурет- Қалыптасқан, еркін және өтпелі токтар R,
2.4 сурет- Қалыптасқан, еркін және өтпелі токтар R,
L тізбекті синусоидалды ЭҚк-ке қосқанда
34)Айнымалы кернеу көзіне қосылған RC тізбегіндегі өтпелі кезең
Тізбек 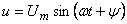 кернеуге қосылады.
кернеуге қосылады.
Сыйымдылықтағы қалыптасқан кернеу
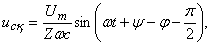 мұнда
мұнда 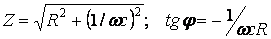 .
.
Сыйымдылықтағы еркін кернеу
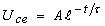 .
.
Сыйымдылықтағы өтпелі кернеу
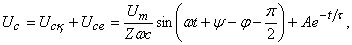
басты жағдайдан шығады  кезде
кезде 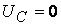 .
.
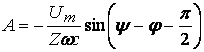 .
.
Сыйымдылықтағы кернеу өзгеруі
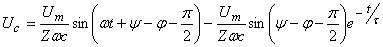 (2.9)
(2.9)
Ток 
10.Активті кедергідегі синусоидалы тоқ.Активті кедергідегі тоқ, кернеу, қуат(лездік және кешенді түрлері). Лездік мәндер графигі. Векторлық диаграммасы.


39.Белгісіз шаманың бейнесінен түпнұсқаны анықтау тәсілдері. Жіктеу формуласы.Өтпелі процестерді классикалық әдіспен есептеу басты жағдай бойынша интегралдаудың тұрақтыларын белгілеу және басты функцияларды және олардың туындыларын табу үшін алгебралық теңдеулердің жүйесін дүркін-дүркін шешуді талап етеді. Бұл жағдай осы әдіспен есептеудің негізгі қиыншылығына жатады. Электр сүлбелер қүрделендірілген сайын және дифференциялды теңдеудің дәрежесі өскен сайын бұл қиыншылықтарда өседі.
Сондықтан, тапсырылған басты жағдайлар бастапқы теңдеулерге кіргізіліп сызықты дифференциалды теңдеулерді шешу әдісті пайдалану қолайлы болады, өйткені бұл әдісте керекті функцияларды табу үшін интегралдаудың тұрақтыларын белгілеудің қажеттігі жоқ болады.
Сызықты дифференциалды теңдеулерді Лапластың түрлендірулерге негізделген операторлық әдіспен интегралдауға болады.
Операторлық әдістің маңызы – түпнұсқа деп аталатын кейбір тапсырылған бір қатарлы шектелген заттың айнымалының  функциясына басқа бейнесі деп аталатын
функциясына басқа бейнесі деп аталатын 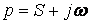 комплексті айнымалының
комплексті айнымалының  функциясы салыстырылады. Функция
функциясы салыстырылады. Функция  әрбір ақырғы уақыт аралықта Дирихле жағдайын қамтамасыз ету керек және
әрбір ақырғы уақыт аралықта Дирихле жағдайын қамтамасыз ету керек және 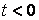 кезде нөлге тең болу керек.
кезде нөлге тең болу керек.
Салыстыру мына формула бойынша өткізіледі
 (5.1)
(5.1)
(5.1) кейіптеме -  функцияның үстінен Лапластың тікелей түрлендіруін көрсетеді.
функцияның үстінен Лапластың тікелей түрлендіруін көрсетеді.
Оны былай белгілейді:
 немесе
немесе 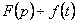 , мұнда
, мұнда  -
-  функцияның Лапластық бейнесі. Кері, егерде
функцияның Лапластық бейнесі. Кері, егерде  бейнесі бойынша
бейнесі бойынша  түпнұсқаны табу керек болса, онда Лапластың кері түрлендіруі қолданады
түпнұсқаны табу керек болса, онда Лапластың кері түрлендіруі қолданады
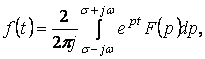 (5.2)
(5.2)
яғни (10.1) интегралды теңдеуді  функцияға қатысты шешу.
функцияға қатысты шешу.
(10.2) интегралды былай белгілеуге болады:
 немесе
немесе  .
.
Түпнұсқадан туындылардың және интегралдардың бейнелері үшін кейіптемелерін (шығарусыз) келтірейік:
Егер де 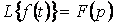 болса, онда (5.3)
болса, онда (5.3)
 (5.4)
(5.4)
 және т.с.с. (5.5)
және т.с.с. (5.5)
Егер де  функция және оның туындылары
функция және оның туындылары 
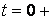 кезде кенет өзгерсе, онда (9.4) және (9.5) кейіптемелерге олардың мәнін осы кенет өзгерісті есепке алып қою керек, яғни нөлдің оң жағында, бұл жағдай олардың аргументтерінде 0+ белгімен көрсетілген. Егер де
кезде кенет өзгерсе, онда (9.4) және (9.5) кейіптемелерге олардың мәнін осы кенет өзгерісті есепке алып қою керек, яғни нөлдің оң жағында, бұл жағдай олардың аргументтерінде 0+ белгімен көрсетілген. Егер де 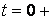 кезде функцияның және оның туындыларының басты мәндері нөлге тең болса, онда бірінші және одан соңғы туындылардың бейнелері өте жеңіл табылады:
кезде функцияның және оның туындыларының басты мәндері нөлге тең болса, онда бірінші және одан соңғы туындылардың бейнелері өте жеңіл табылады:
 және т.с.с. (5.6)
және т.с.с. (5.6)
Тұп нұсқаның интегралдық бейнелерінің түрі:
 (5.7)
(5.7)
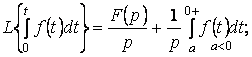 (5.8)
(5.8)
Егерде интеграл 
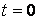 кезде кенет өзгерсе, онда оның мәнін нөлдік оң жағынан алу керек, бұл жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.
кезде кенет өзгерсе, онда оның мәнін нөлдік оң жағынан алу керек, бұл жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.
Жіктеудің теоремасы
Бейне  (5.9) дұрыс бөлшек түрде берілсін, алымның және бөлгіштің жалпы түбірлері жоқ.
(5.9) дұрыс бөлшек түрде берілсін, алымның және бөлгіштің жалпы түбірлері жоқ.  функцияның полюстерінің орыны
функцияның полюстерінің орыны 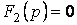 (10.10) теңдеудің түбірлерімен белгіленеді. (5.10) теңдеудің
(10.10) теңдеудің түбірлерімен белгіленеді. (5.10) теңдеудің 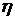 түбірлерін
түбірлерін  деп белгілейміз.
деп белгілейміз.
Екі жағдай болуы мүмкін: а) барлық түбірлер жай; б) кейбір немесе барлық түбірлер еселі.
а) жай түбірлердің жағдайы
Өте жай жағдайда бейне радионалды бөлшек түрінде болады:
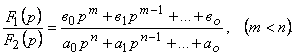 (5.11)
(5.11)
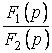 бөлшек қысқарылмайды, яғни
бөлшек қысқарылмайды, яғни  және
және 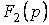 мүшелердің жалпы түбірлері жоқ, ал
мүшелердің жалпы түбірлері жоқ, ал 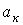 және
және 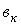 - заттық сандар. (5.11) бейненің түпнұсқасын жікте теормасы деп аталатын кейіптеме бойынша табуға болады:
- заттық сандар. (5.11) бейненің түпнұсқасын жікте теормасы деп аталатын кейіптеме бойынша табуға болады:
 (5.12)
(5.12)
Мұнда pк сипаттамалы теңдеудің, яғни 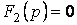 теңдеудің жай түбірлері, бір түбір нөлге тең болуы мүмкін.
теңдеудің жай түбірлері, бір түбір нөлге тең болуы мүмкін.
Егер де бір түбір нөлге тең болса, яғни бөлгіш ішінде (5.11) р көбейткіш бар болса, онда жіктеу теореманың басқа түрі қолданады.
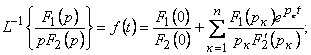 (10.13)
(10.13)
б) еселі түбірлердің жағдайы
Егер де көп мүшелі 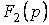 түбірлерінің ішінде еселі түбірлер болса, онда жіктеу теореманы (5.12) және (5.13) формулаға ұқсасты жасауға болады, бірақ оң жағында қосындымен (бір қосынды түбірлер саны бойынша, ал екінші әрбір түбір үшін оның еселік реттігімен).
түбірлерінің ішінде еселі түбірлер болса, онда жіктеу теореманы (5.12) және (5.13) формулаға ұқсасты жасауға болады, бірақ оң жағында қосындымен (бір қосынды түбірлер саны бойынша, ал екінші әрбір түбір үшін оның еселік реттігімен).
Сонымен, 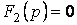 теңдеуде еселі түбірлер болса, онда
теңдеуде еселі түбірлер болса, онда 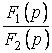 кесінді бойынша тұп нұсқау мына формула бойынша есептеледі:
кесінді бойынша тұп нұсқау мына формула бойынша есептеледі:
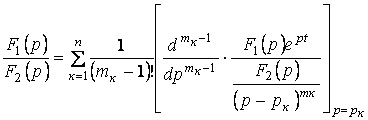
(5.14)
Шаршы жақшаның бөлгішіндегі көріністі алдымен  шамаға қысқартып, содан кейін дифференциялдау керек.
шамаға қысқартып, содан кейін дифференциялдау керек.
Егер де 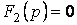 теңдеуде бір мезгілде жай және еселі түбірлер болса, онда жай түбірлерге сәйкесті қосындыларды (5.12) және (5.13) формулалар, ал еселі түбірлер үшін (5.14) формула қолданады.
теңдеуде бір мезгілде жай және еселі түбірлер болса, онда жай түбірлерге сәйкесті қосындыларды (5.12) және (5.13) формулалар, ал еселі түбірлер үшін (5.14) формула қолданады.
7. Түйінді потенциалдар әдісімен токтарды анықтау.Кирхгофтың 1 заңына нергіжделген шартты түрде 1 түйіннің потенциалын 0-ге теңестіреміз. Сонда қалған отенциалдар үшін теңдеулер жүйесі келесі түрді қабылдайды.Негізгі потнециал «+» қалғаны «-» (Сурет лекцияда берілген) 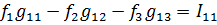 -
- 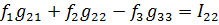 -
- 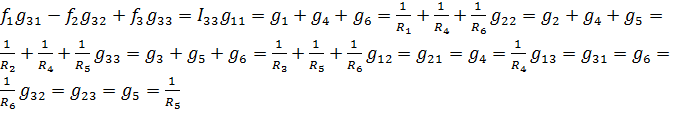 Түйінен шықса «-» кірсе «+»
Түйінен шықса «-» кірсе «+» 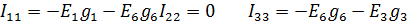 Кез келген әдіспен белгісіз
Кез келген әдіспен белгісіз  потециалдарын анықтаймыз. Сонда тармақтағы токтар Ом заңы бойынша анықталады.
потециалдарын анықтаймыз. Сонда тармақтағы токтар Ом заңы бойынша анықталады.
38. Екінші реттік тармақталған электр тізбектеріндегі өтпелі кезеңдерді классикалық әдіспен есептеу реті.Белгісіз шама өтпелі ток болсын делік:
1) Электр тізбегі үшін ТБШ анықтаймыз
2) Өтпелі токтың қалыптасқан құраушысын анықтаймыз. Қалыптасқан құраушы комутациядан кейінгі режим үшін анықталады.
3) Комутациядан кейінгі режим үшін тізбектің кіріс кедергісінің Z(p) теңдеуін құрамыз. Оны 0-ге теңестіреміз. Бұл кезде реактивті кедергілер pL және 1/pC операторлық түрде көрсетіледі:jwL=pL 1/jwC=i/pC p=jw
4) Z(p) өрнегін түрлендіреміз, соңғы өрнекке берілген параметрлердің мәндерін қоямыз. Содан кейін p1 және р2 анықтаймыз. р1 және р2 мәндері өтпелі тоқтың еркін құраушысының түрін анықтайды.
Д>0
p1,p2-“-” таңбасы нақты сан
іер=A1еp1*t+A2ep2*t
Д=0
іер=(A1+A2t)ept
p1=p2<0
Д<0 p1,2=-a+-jw
iер=Aeatsin(wt+ф)
5) Интегралдау тұрақтыларын анықтау үшін тағы бір теңдеу қажет. Сондықтан өтпелі шаманың бірінші ретті туыныдысын анықтаймыз.
i’Lер=p1A1ep1*t+p2A2ep2t
i’Lер=aAeatsin(wt+ф)+wAeatcos(wt+ф)
6) Өтпелі шаманың және оның туындысының t=0 кезіндегі теңдеулерін құрамыз
i’ер=p1A1+A2p2 iер=A1+A2
i’ер=aAsinф+wAcosф iер=Asinф
7) ТБШ-ны ескере отырып, Кирхгоф заңдары бойынша t=0 кезіндегі теңдеулерді құрамыз. Ол теңдеуден өзімізге қажетті өтпелі шаманың бастапқы мәнін анықтаймыз. Берілген тізбек үшін Кирхгоф заңдарын комутациядан кейінгі режим үшін анықтаймыз. Анықталған өтпелі шаманың бастапқы мәнің және оның туындысын нөлдік мәнін жоғардағы теңдеуге қойып, интергралдау тұрақтысын анықтаймыз. Сонда өтпелі шама қалыптасқан және еркін құраушыларының қосындысына тең болады.
i(t)=iқ+iер
U(t)=Uқ+Uер
40. Екінші реттік тармақталған электр тізбектеріндегі өтпелі кезеңдерді операторлық әдіспен есептеу реті.Өтпелі кезеңдерді операторлық әдіспен есептеу 3 кезеңнен тұрады. Бірінші кезеңде функциялардың түпнұсқалары үшін Кирхгоф заңдары бойынша құрастырылған дифференциалды теңдеулер жүйесі Лапластың түрлендіруін қолдана отырып осы функциялардың операторлық бейнелерінен құралатын алгебралық теңдеулер жүйесіне ауысады.
Екінші кезеңде белгісіз шамаға қатысты алгебралық операторлық теңдеулер жүйесі шешіледі. Белгісіз шаманың F(p) операторлық өрнегі шығады.
Соңғы үшінші кезеңде анықталған F(p) өрнегінен оған сәйкес келетін f(t) функциясын анықтау орындалады.
Теория жүзінде F(p) бейнесінен f(t) түпнұсқасын анықтау- Лапластың кері түрлендіру функциясы бойынша анықталады.
26.Жұлдызша жалғанған симметриялы емес үшфазалы тізбекті есептеу.Симметриялы режімді есептеумен танысу үшін 8.4 суреттегі симметриялы тізбектегі токтардың есептелу ретін қарастырамыз. Қуат көзінің қысқыштарындағы кернеу симметриялы болсын және берілген, сондай-ақ тізбектегі 1,2,3 және 4 элементтердің кедергілері белгілі болсын. Есептеуді бастамас бұрын сұлбаны түрлендіріп алған дұрыс, яғни 4 элементті және үшбұрышша байланысқан қуат көзін жұлдызша байланысына ауыстырамыз. Симметриялы жұлдызшадағы фазалық кедергі эквивалентті симметриялы үшбұрыштың фазалық кедергісінен 3 есе аз. Жұлдызша байланысқан эквивалентті қуат көзінің фазалық кернеуі, берілген сызықтық кернеуден есе аз. Сол себепті 8.5 суретте көрсетілген сұлбаны аламыз. Симметриялы режімде барлық нейтрал нүктелер бірдей потециалға ие болады. Сондықтан сұлбаның режимін бұзып алмай, оларды кедергісіз сымдармен байланыстырамыз (үзік сызықтар арқылы көрсетілген). Содан кейін сұлбадан екі фазаны алып тастаймыз, мысалы В және С содан кейін 8.6 суреттегі сұлбаға өтеміз.
8.4 сурет- Симметриялы режим 8.5 сурет- алмастыру сұлбасы  |
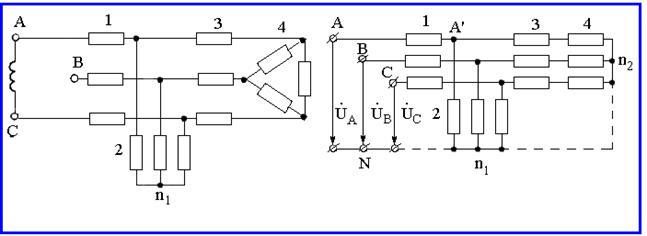
8.6 сурет- Соңғы есептік сұлба
2.2 және 2.3 суреттерде көрсетілген бірдей сұлбалар үшін А' түйіні және АА'n1N мен А'n2n1А' контурларына құрылған Кирхгоф заңының теңдеулері нақты, сондай-ақ А фазасындағы ток пен кернеу екі сұлба үшінде бірдей. А фазасындағы токтарды бірфазалы сұлба үшін есептеу өте жеңіл (8.6 суретті қара), мысалы алдындағы түрленген әдіс бойынша А'n2 және А'n1 тармақтарының эквивалентті кедергілерін параллель байланысқа ауыстыру арқылы. В және С фазасындағы токтарыдың модулі дәл А фазасындағыдай болады. 4 үшбұрыштың тармақтарындағы токтар 3 элементтегі токтармен салыстырғанда есеге аз (кез-келген топтағы әр элементтің токтарының фазалық ығысуының қатынасы дәл сол топтағы басқа элементтермен салыстырғанда бірдей + немесе бұрышқа тең болады).
23.Жұлдызша жалғанған симметриялы үшфазалы тізбекті есептеу.Үш фазалы тізбек оның тармақтарының кешенді кедергілері өзара тең болған жағдайда симметриалы д.а. Егер үш фазалы симметриалы тізбекке симметриалы кернеулер келтіретін болсақ, онда сызықты сымдар бойымен симметриалы токтар өтеді. Симметриалы режимде нейтралды ток 0-ге тең. IN=IA+IB+IC IA=  IB=
IB=  IC=
IC= 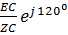
UAB=EA-EB UBC=EB-EC UAC=EA-EC
Симметриалы үш фазалы режим кезінде
P=3*Uф*Iфcosф Вт Активтік қуат
P=3*Uф*Iфsinф ВАр Реактивтік қуат
P=3*Uф*Iф ВА
Фазалардың жұлдызша жалғануы кезінде сызықты токтар фазалы токтарға тең болады. Ic=Iф. IA=Iф. Uc= 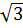 Uф
Uф
24.Жұлдызша жалғанған үшфазалы тізбек. Үшфазалар шамалар жүйесі. Бір-біріне қатысты фаза бойынша жылжыған арасында бірдей жиілікті кернеулер пайда болған бірнеше шықпасы бар қорек көздері - көп фазалы қорек көздері д.а.
АВС фазаларының ЭҚК бір-біріне қатысты 1/3 периодына жылжыған. ЭҚК-тердің бастапқы фазасы 0-ге тең болады. ФА=0 ЕА=ЕМ* 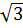 sin
sin 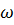 t. ЕВ=ЕМ*
t. ЕВ=ЕМ* 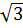 sin(
sin( 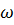 t-
t-  ) ЕС=ЕМ*
) ЕС=ЕМ* 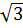 sin(
sin( 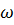 t+
t+  ).
).
Үш фазалы генератордың ЭҚК-нің лездік мәндерінің графигі.
Векторлық диаграмма салу үшін ЭҚК-ң кешенді мәндерін анықтаймыз. ЕA= 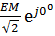 ЕB=
ЕB=  Еc=
Еc= 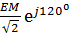 Векторлық диаграмма
Векторлық диаграмма
Үш фазалы тізбекте генераторлардың, трансформаторлардың, орамдардың және қабылдағыштардың 2 түрлі жалғанулары болады. 1)үшбұрышша 2)жұлдызша
Жұлдызша жалғану кезінде фазалық қорек көздерінің ұштары бір жалпы нүктелермен жалғастырылады. Қорек көздерінің және қабылжағыштар жұлдызының ортақ нүктелері нейтралды нүктелер н/е нолдік нүктелер д.а. Нейтралды нүктелерді қосатын сым- нолдік сым н/е нейтралды сым д.а. Қорек көздері мен қабылдағыштарды бір-бірімен жалғастыратын қалған сымдар – сызықты сымдар д.а.
27. Жұлдызша жалғанған үшфазалы тізбектің апатты жағдайын есептеу
11. Индуктивтіктегі синусоидалы тоқ.

 Кернеудің лездік мәні
Кернеудің лездік мәні  (индуктивтілік кешенді кедергі)
(индуктивтілік кешенді кедергі)
20.КЕРНЕУ РЕЗОНАНСЫ. РЕЗОНАНСТЫҚ ТӘУЕЛДІЛІКТЕР.Айнымалы ток тізбегінің толық кедергісі 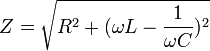 өрнегі мен анықталатыны белгілі болды. Бұл формуладағы индуктивтік кедергімен сыйымдылық кедергі бір-біріне тең болса, толық кедергі ең аз мәнге ие болатынын көреміз. Сонымен, егер
өрнегі мен анықталатыны белгілі болды. Бұл формуладағы индуктивтік кедергімен сыйымдылық кедергі бір-біріне тең болса, толық кедергі ең аз мәнге ие болатынын көреміз. Сонымен, егер  болса. Мұндай жағдайда ток пен кернеудің тербеліс фазаларының айырымы:
болса. Мұндай жағдайда ток пен кернеудің тербеліс фазаларының айырымы: 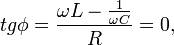 яғни токпен кернеу тербелістері бірдей фазада жүреді. Активті кедергі дегі кернеу тізбекке түсірілген кернеуге тең
яғни токпен кернеу тербелістері бірдей фазада жүреді. Активті кедергі дегі кернеу тізбекке түсірілген кернеуге тең 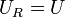 , ал конденсатордағы
, ал конденсатордағы 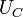 кернеумен катушкадағы
кернеумен катушкадағы  кернеу амплитудалары бір-біріне тең және фазалары қарама-қарсы. Ом заңы бойынша ток амплитудасы
кернеу амплитудалары бір-біріне тең және фазалары қарама-қарсы. Ом заңы бойынша ток амплитудасы  Бұл өрнектен, егер активті кедергі аз болса, ток күшінің амплитудасы өте үлкен мәнге ие болатынын көреміз. Жоғарыда сипатталған құбылыс электр тізбегіндегі резонанс деп аталады. Резонанс байқалу үшін тізбекке түсірілген кернеудің жиілігі (2.17) өрнегін қанағаттандыру керек:
Бұл өрнектен, егер активті кедергі аз болса, ток күшінің амплитудасы өте үлкен мәнге ие болатынын көреміз. Жоғарыда сипатталған құбылыс электр тізбегіндегі резонанс деп аталады. Резонанс байқалу үшін тізбекке түсірілген кернеудің жиілігі (2.17) өрнегін қанағаттандыру керек: 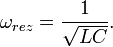 Біз активті кедергісі идеал тербелмелі контурдың меншікті тербелістерінің жиілі
Біз активті кедергісі идеал тербелмелі контурдың меншікті тербелістерінің жиілі 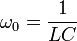 өрнегіменанықталатынынбілеміз. Олайболса, электртізбегіндерезонанстізбеккетүсірілгенсыртқыпериодтыкернеудіңжиілігітізбектіңменшіктіжиілігінетеңболғандабайқалады
өрнегіменанықталатынынбілеміз. Олайболса, электртізбегіндерезонанстізбеккетүсірілгенсыртқыпериодтыкернеудіңжиілігітізбектіңменшіктіжиілігінетеңболғандабайқалады  Осыкездекатушкадағыиндуктивтіккедергіконденсатордыңсыйымдыльщкедергісінетеңболады:
Осыкездекатушкадағыиндуктивтіккедергіконденсатордыңсыйымдыльщкедергісінетеңболады: 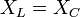 . Активтікедергінеғұрлымазболса, токкүшініңамплитудасысоғұрлымүлкен.
. Активтікедергінеғұрлымазболса, токкүшініңамплитудасысоғұрлымүлкен.
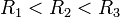 . Егерактивтікедергішексізазболса , токамплитудасышексізартады →. Активті, индуктивтікжәнесыйымдылықкедергілертізбектейжалғанғандабайқалатынрезонанстыкернеулеррезонансынемесетізбектірезонансдепатайды. Себебірезонанскезіндетоктыңөсуіменқатар, катушкаменконденсатордағыкернеулердекүртөседі. Тізбектейжалғанғанкездеконденсаторменкатушкадағыкернеулерқарама-қарсыфазадатербеледі, алтізбектіңбарлықэлементіарқылыөтетінтоктыңбағытыбірдей, сондықтанболғанда
. Егерактивтікедергішексізазболса , токамплитудасышексізартады →. Активті, индуктивтікжәнесыйымдылықкедергілертізбектейжалғанғандабайқалатынрезонанстыкернеулеррезонансынемесетізбектірезонансдепатайды. Себебірезонанскезіндетоктыңөсуіменқатар, катушкаменконденсатордағыкернеулердекүртөседі. Тізбектейжалғанғанкездеконденсаторменкатушкадағыкернеулерқарама-қарсыфазадатербеледі, алтізбектіңбарлықэлементіарқылыөтетінтоктыңбағытыбірдей, сондықтанболғанда 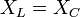 , яғнирезонанскезіндекезкелгенуақытмезетіүшін
, яғнирезонанскезіндекезкелгенуақытмезетіүшін  . Ал
. Ал  екенінескерсек, индуктивтіккатушкадағыжәнеконденсатордағыкернеутербелістерініңамплитудасыбылайесептеледі:
екенінескерсек, индуктивтіккатушкадағыжәнеконденсатордағыкернеутербелістерініңамплитудасыбылайесептеледі:  Сонымен
Сонымен  Тербелмеліконтурда
Тербелмеліконтурда  қатынасыорындалады, сондықтанконденсаторменкатушкадағыкернеулертізбеккетүсірілгенкернеуденартықжәнеазайғансайынартатүседі. Жалпы, активтікедергісі аз болғандағана резонанс құбылысынқарастырады. Активтікедергініңүлкенмәндеріндеісжүзінде резонанс байқалмайды (2.20-сурет). Кернеулеррезонансынкандай да бірберілгенжиіліктегікернеутербелістерінкүшейтуүшінпайдаланады. Кернеудіңрезонанстықөсуірезонанстықжиіліккежуықөте аз интервалдажүретінболғандықтан, көптеген сигнал ішіненжиілігісолрезонанстықжиіліккежуықбірғана сигнал бөліпалынады. Мысалы, радиоқабылдағыштакеректітолқындыосылайшаіздейді. Катушкалары мен конденсаторлары бар электржүйелерініңизолядияларынесептегенде де кернеулеррезонансынескерукерек, әйтпесеэлектртесілулеріболуымүмкін. Механикалықтербелістердід резонансы сыртқыпериодтыкүштіңжиілігітербелмеліжүйеніңменшіктіжиілігімендәлкелгендебайқалатынынбілеміз. Механикалықтербелістерде үйкеліскүштеріэлектромагниттіктербелістердегіактивтікедергініңрөлінатқарады
қатынасыорындалады, сондықтанконденсаторменкатушкадағыкернеулертізбеккетүсірілгенкернеуденартықжәнеазайғансайынартатүседі. Жалпы, активтікедергісі аз болғандағана резонанс құбылысынқарастырады. Активтікедергініңүлкенмәндеріндеісжүзінде резонанс байқалмайды (2.20-сурет). Кернеулеррезонансынкандай да бірберілгенжиіліктегікернеутербелістерінкүшейтуүшінпайдаланады. Кернеудіңрезонанстықөсуірезонанстықжиіліккежуықөте аз интервалдажүретінболғандықтан, көптеген сигнал ішіненжиілігісолрезонанстықжиіліккежуықбірғана сигнал бөліпалынады. Мысалы, радиоқабылдағыштакеректітолқындыосылайшаіздейді. Катушкалары мен конденсаторлары бар электржүйелерініңизолядияларынесептегенде де кернеулеррезонансынескерукерек, әйтпесеэлектртесілулеріболуымүмкін. Механикалықтербелістердід резонансы сыртқыпериодтыкүштіңжиілігітербелмеліжүйеніңменшіктіжиілігімендәлкелгендебайқалатынынбілеміз. Механикалықтербелістерде үйкеліскүштеріэлектромагниттіктербелістердегіактивтікедергініңрөлінатқарады

17. Контурлық тоқтар әдісімен синусоидалы ток тізбектерін есептеу.Берілген тізбекте контурлардың бойымен өтетін кешендік контурлық тоқтарды енгіземіз . олардың бағытын өз еркімізбен таңдаймыз . сол КТ қатысты теңдеу жүйесін құрып , белгісіз кешенді токтарды анықтаймыз.
 (
( 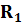 +
+ 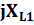 -
- 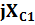 +
+  +
+ 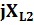 )-
)- 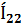 (
(  +
+ 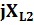 )=
)= 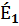
-  (
(  +
+ 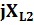 )+
)+ 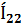 (
(  +
+ 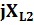 +
+ 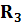 -
- 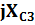 )=
)= 
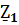 =
= 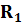 +
+ 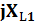 -
- 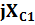
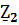 =
=  +
+ 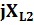
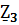 =
= 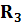 -
- 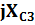
 (
( 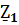 +
+ 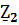 )-
)- 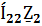 =
= 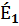
- 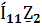 +
+ 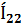 (
( 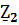 +
+ 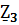 )=
)= 
Сонда тармақтағы кешенді тоқтар келесі түрде анықталады 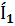 =
= 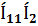 =
=  -
- 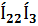 =
= 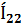
5 .Тұрақты ток тізбегін контурлық тоқтар әдісімен есептеу.Контурлық токтар әдісі. Контурлық ток-алынған контурдың әр бөлігі үшін бірдей болатын есептеу шамасы. Есептеуді мына ретпен жүргізеді:а)тізбектің барлық тәуелсіз контурындағы контурлық токтардың бағытын бірдей етіп алады(сағат тілі бойынша немесе керісінше);б) контурдың айналу бағытын да сондай бағытпен белгілейді.Кирхгофтың екінші заңы бойынша контурдың әрқайсысына тәуелсіз теңдеулер құрылады. Бұл үшін әрбір контурда кездесетін бөліктердегі ЭҚК-імен контурлық токтардың теңдеу құрылып жатқан контурға қатыстығын қарастырады;в)алынған теңдеулер жүйесін шешіп, контурлық токтарды табады, ол арқылытармақтардағы негізгі токтарды есептейді.Контурлық токтар және олардың айналым бағыттары сағат тілінің бағытымен алынған.1231контуры үшін: 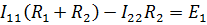 1361контур үшін:
1361контур үшін: 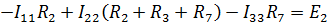 3463контур үшін:
3463контур үшін:  4564контур үшін:
4564контур үшін:  Тармақтардағы негізгі токтарды табу үшін мынаны ескеру керек, егер кез-келген тармақтан тек бір ғана контурлық ток өтсе, негізгі ток контурлық токтың өзіне тең, ал тармақтан бірнеше контурлық ток өтсе, онда негізгі ток осы контурлық токтардың алгебралық қосындысына тең.
Тармақтардағы негізгі токтарды табу үшін мынаны ескеру керек, егер кез-келген тармақтан тек бір ғана контурлық ток өтсе, негізгі ток контурлық токтың өзіне тең, ал тармақтан бірнеше контурлық ток өтсе, онда негізгі ток осы контурлық токтардың алгебралық қосындысына тең.
 .
.
21. Өзара индуктивті байланысқан элементтер, өзіндік және өзара индукция ЭҚК.Суретте (2) магнит ағынының ол арқылы ағып ағымдағы пропорционалды бірінші катушкалар W (1) және W бірқатар бар катушкалар екі кезекпен көрсетеді. Ағынының бөлігі катушкалар еніп, екінші катушкалар ток арқылы әсер етеді.
Сол сияқты, магнит ағынының бірінші, екінші катушкалар орамасының өтеді.
Жалғасатын (немесе магнитті байланысқан) - Бұл бухталарда индуктивті деп аталады.
Қатынасы айқындалатын тіркелу коэффициенті к сипатталады екі тізбек элементтерінің индуктивтік дәрежесі:
= <1
онда M - тізбек элементтерінің өзара индуктивтілік, H.
- Индуктивтілік элементтері, H.
Жалпы, бірінші және екінші катушек өзара индуктивтілік бірінші катушкалар ағымдағы екінші қосымша катушкалар ағынының коэффициенті болып табылады:
12 Индекс өзара индуктивтілік екінші катушкалар магнит ағынының бірінші катушкалар туындаған екенін көрсетеді.
Тәжірибе көрсеткендей, бұл:
Сызықты электр тізбектерінің өзара индуктивтілік бағыты мен ағымдағы мәндеріне тәуелді емес, және олардың өзара raspolozheniem.Induktivnost катушкалар ғана бухталарда жобалау бойынша анықталады:
Магниттік тізбектерді теңдеулер құрастыру қарсы сәйкес немесе өзін-өзі және өзара индуктивтілік индуктивтілік ағымын бағыттап, білу қажеттігін байланысты. Сіз ядро катушкалар орамасының бағытын білу және оларға ағымдардың оң бағытын таңдаған болса, бұл туралы дұрыс қорытынды жасауға болады
Тпелі үрдістерді Дюамель интеграл өрнегімен есептеу.Мейлі еркінше пассивтік сызықты екіұштық уақыттан бастап үздіксіз өзгеріп тұрған кернеу көзіне қосылсын (6.2 сурет). Екі ұштықтың қандайда болған тармағында кілт тұйықталғанда ток -ді (немесе -ды) табу керек.
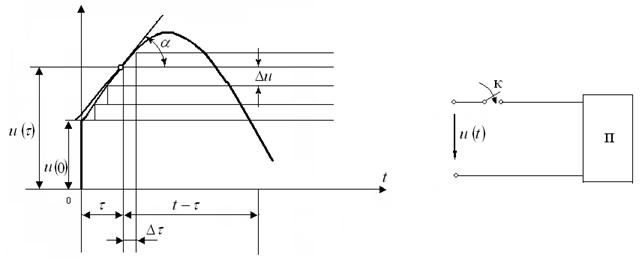
6.2 Сурет
Есепті екі кезеңге бөлеміз. Алдымен керекті шаманы екіұштықты жекелеген кернеудің ырғағына қосқан кезде табамыз (кернеу тұрақты және сан бойынша бірге тең).
Жекелеген ырғақ (жекелеген сатылы әсер ету) жекелеген сатылы функциямен беріледі –6.3-суреттегі бейнеленген 1(t) Хевисайдтың функциясымен.

6.3 Сурет
Электр тізбектер теориясының көзқарасы бойынша тізбектің кірісінде әрекет істейтін жекелеген тұрақты кернеу (немесе ток) 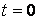 + уақыт кезінде.
+ уақыт кезінде.
Сонымен 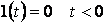 кезінде;
кезінде;
 кезінде. (6.3.)
кезінде. (6.3.)
Жекелеген ырғақ әсер еткендегі сан бойынша ізделіп отырған токқа (немесе кернеуге) тең 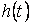 функция өтпелі функция деп аталады. Бұл тізбектің жекелеген ырғаққа әсерлістігі.
функция өтпелі функция деп аталады. Бұл тізбектің жекелеген ырғаққа әсерлістігі.
Мысалы, R, L – тізбек үшін кернеудің өтпелі функциясы  ал RC-тізбек үшін кернеудің өтпелі функциясы
ал RC-тізбек үшін кернеудің өтпелі функциясы 
Өтпелі функцияны, қандайда болған екіұштықтық сүлбесі болғанда, классикалық немесе операторлық әдіспен табуға болады. Сонымен, есептеу кезде 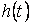 функция белгілі деп санаймыз.
функция белгілі деп санаймыз.
Пассивтік екіұштық қосылып тұрғандықтан 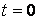 кезде токтар және кернеулер тармақтарда нөлге тең, яғни t<0 кезде
кезде токтар және кернеулер тармақтарда нөлге тең, яғни t<0 кезде  .
.
Тоқты есептеу жағдайын қарап шығайық.
Үздіксіз өзгеріп тұрған 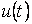 кернеуді
кернеуді  тура бұрышты ырғақтары бар сатылы функциямен алмастырамыз (6.4 сурет).
тура бұрышты ырғақтары бар сатылы функциямен алмастырамыз (6.4 сурет).
Онда кернеу өзгерудің процесін 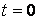 кезде
кезде  тұрақты кернеуді қосу деп, ал содан кейін бірбірінен
тұрақты кернеуді қосу деп, ал содан кейін бірбірінен 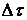 уақыт аралыққа ығысқан
уақыт аралыққа ығысқан  элементарлы тұрақты кернеулердің қосылуы деп көрсетуге болады. Кернеудің қисығына өскенде + таңба, ал төмендегенде – таңба қойылады.
элементарлы тұрақты кернеулердің қосылуы деп көрсетуге болады. Кернеудің қисығына өскенде + таңба, ал төмендегенде – таңба қойылады.
Ізделіп жатқан токтың  тұрақты кернеуден t уақыт кездегі құрастырушысы
тұрақты кернеуден t уақыт кездегі құрастырушысы  тең. Токтың құрастырушысы t уақыт кезде
тең. Токтың құрастырушысы t уақыт кезде 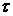 уақыт кезде қосылатын
уақыт кезде қосылатын  ырғақты кернеуге тең
ырғақты кернеуге тең 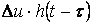 . Мұнда өтпелі функцияның аргументі ретінде уақыт
. Мұнда өтпелі функцияның аргументі ретінде уақыт 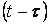 алынады. Оған себеп болатыны -
алынады. Оған себеп болатыны -  кернеудің ырғағының әрекеті кілт тұйықталғаннан кейін
кернеудің ырғағының әрекеті кілт тұйықталғаннан кейін 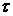 уақыт өткенде басталады.
уақыт өткенде басталады.
Кернеудің элементарлы ырғағы

Сондықтан токтың ізделіп жатқан құрастырушысы
 (6.4)
(6.4)
Кернеудің элементарлы ырғақтары 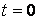 -ден t кездегі уақыт аралықта қосылады. Сондықтан, барлық ырғақтардан токтың құрастырушыларын жинақтап,
-ден t кездегі уақыт аралықта қосылады. Сондықтан, барлық ырғақтардан токтың құрастырушыларын жинақтап,  кезде шекке өтіп және
кезде шекке өтіп және  басты кернеудің ырғағынан токтың құрастырушысын есепке алып табамыз.
басты кернеудің ырғағынан токтың құрастырушысын есепке алып табамыз.
 (6.5)
(6.5)
(6.5) кейіптеме Дюамельдің интегралы деп аталады.
42. Өтпелі кезеңдерді спекралды әдіспен есептеу негіздері.
30.Өтпелі кезеңдердің пайда болуы.
9.Синусоидалы ток тізбектері. Синусоидалы шамалар.Синусоидалы - деп sin заңы б/ша өзгеретін ж/е уақыт б/ша өзгер-н токты айт-з. Синусоидалық токтың лездік мәні мына өрнек-н анық-ды:i=Imsin(2πt/T+ψ)= Imsin(ωt+ψ), мұнд Im –ток амплитудасы, яғни токтың ең үлкен мәні; синус аргументі 2πt/T+ψ–фаза д.а. Бұрыш ψ-бастапқы уақыт мезгіліндегі (t=0) фазасына тең, сонд-н оны бастапқы фаза д.а.Синусоидалы ток тізб-ң элемент-і:1.активті кедергі R;Бұл токтың лездік кернеуі u=Umsinωt.Ом заңы б/ша u=iR=ImRsin ωt; Тұж-а: активті кедергіде ток пен кернеу фаза б/ша сәйкес келеді.активті кедергіге келіп түсетін қуат келесі өрнекпен анықт-ы: P=ui=UmsinωtImsinωt=UIsin2ωt=UmIm(1-cos2ωt)/2. Син-ы ток тізб-і индуктивтілік: ХL=ωL=2πfL; UL=LdI/dt кернеу-ң лездік мәні. Индуктивтіліктегі кернеу векторы ток векторынан 90̊ озып отырады. Сыйымдылық кедергі: Хс=1/ωС; u=1/c 0ʃπίdt. Сыйымд-қ кедергіде ток векторы кернеу вект-н 90̊-қа озады.
Синусоидалыэлектршамалар – электр тізбекте кернеудің және токтын лездік шамалары тең уакыт аралык саиын каиталанатын процесс периоды деп аталады.Периодты шаманын мәні кайталанатын ен аз уакыты период деп аталады.Синусоидалы шаманын озгеріп тұрган мәнін белгілейтін шама 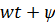 фаза депаталады .Уакытагымыбойынша фаза оседі. 2πшамага фаза оскенненкеинсинусойдалышаманынозгеру циклі каиталанады
фаза депаталады .Уакытагымыбойынша фаза оседі. 2πшамага фаза оскенненкеинсинусойдалышаманынозгеру циклі каиталанады
19.Синусоидалы ток тізбектері үшін қуаттар тепе-теңдігі.Энергияның сақталу заңынан шығатыны-ол кез келген тізбекте лездік және активті қуаттарының да тепе-теңдіктері сақталады.Энергия көздерінен беріліп тұрған барлық қуаттарының қосындысы,барлық қабылдағыштардағы қабылданған қуаттардың қосындысына тең.Комплекстік үшін де тепе-теңдіктің сақталатынын көрсетеді.
 =
= 
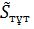 =
= 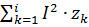
 =
= 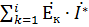
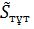 =
= 
 =
= 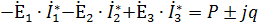
13. Синусоидалы шамалардың лездік және комплексті түрлері. Кернеу мен токтың әсерлік мәні.Синусоидалы - деп sin заңы б/ша өзгеретін ж/е уақыт б/ша өзгер-н токты айт-з. Синусоидалық токтың лездік мәні мына өрнек-н анық-ды:i=Imsin(2πt/T+ψ)= Imsin(ωt+ψ), мұнд Im –ток амплитудасы, яғни токтың ең үлкен мәні; синус аргументі 2πt/T+ψ–фаза д.а. Бұрыш ψ-бастапқы уақыт мезгіліндегі (t=0) фазасына тең, сонд-н оны бастапқы фаза д.а.Синусоидалы ток тізб-ң элемент-і:1.активті кедергі R;Бұл токтың лездік кернеуі u=Umsinωt.Ом заңы б/ша u=iR=ImRsin ωt; Тұж-а: активті кедергіде ток пен кернеу UIsin2ωt=UmIm(1-cos2ωt)/2. Син-ы ток тізб-і индуктивтілік: ХL=ωL=2πfL; UL=LdI/dt кернеу-ң лездік мәні. Индуктивтіліктегі кернеу векторы ток векторынан 90̊ озып отырады. Сыйымдылық кедергі: Хс=1/ωС; u=1/c 0ʃπίdt. Сыйымд-қ кедергіде ток векторы кернеу вект-н 90̊-қа озады.фаза б/ша сәйкес келеді.активті кедергіге келіп түсетін қуат келесі өрнекпен анықт-ы: P=ui=UmsinωtImsinωt
12.Сыйымдылықтағы синусоидалы тоқ.Егер де С сыйымды лықтағы кернеу синусойдалы болса,  онда тоқ:
онда тоқ:
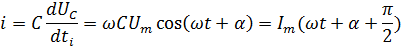
көрініс көрініс көрсетіп тұр: тоқ  ынта салынған кернеуден
ынта салынған кернеуден  бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.Фазалық ығысу:
бұрышқа озып тұр, яғни тоқтың нөлдік мәніне кернеудің максималды мәні сәйкес.Фазалық ығысу: 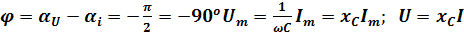
 –сыйымдылық кедергі, ал оған кері шама bC=
–сыйымдылық кедергі, ал оған кері шама bC= 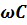 – сыйымдылық өткізгіштік деп аталады. Сонымен,
– сыйымдылық өткізгіштік деп аталады. Сонымен, 
Сыйымдылықтағы лезді қуат:
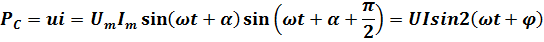
Бұл қуат амплитудасы UI, ал бұрыштық жиілігі 2 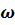 тең синусойдалы заң бойынша тербеленеді, яғни көрініс
тең синусойдалы заң бойынша тербеленеді, яғни көрініс  сияқты.Сыйымдылықтың электр өрісінің энергиясы:
сияқты.Сыйымдылықтың электр өрісінің энергиясы:
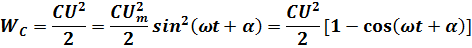
0-ден  – ге дейін шектерде бұрыштық жиілігі
– ге дейін шектерде бұрыштық жиілігі  -мен периодикалы өзгеріп тұрады.
-мен периодикалы өзгеріп тұрады.
Көзбен сыйымдылықтың арасында энергияның тербеленуі өтеді, ал сыйымдылыққа түсетін активтік қуат нөлге тең. Сыйымдылық кедергіні былай табуға болады: 
37. Тармақталмаған RLC – тізбегіндегі өтпелі кезең.R, L, С тізбек осы ЭҚК-ке қосылғанда (3.10-сурет) өтпелі процес (1.3) дифференциалды теңдеу бойынша зерттеледі.
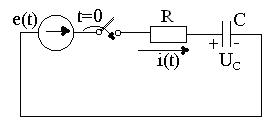
3.1сурет - R, L, С тізбекті е(t) кернеуге қосу
 . (3.1)
. (3.1)
Бұған сәйкес сипаттамалы теңдеу
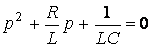 .
.
Оның түбірлері
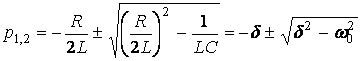 . (3.2)
. (3.2)
мұнда 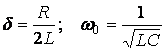 - резонансты жиілік (2.9) бойынша
- резонансты жиілік (2.9) бойынша  .
.
Тізбектегі ток қалыптасқан және еркін токтардың қосындысы.
 (3.3)
(3.3)
Қалыптасқан тоқ берілген е(t) ЭҚК-ке сәйкес табылады, ал еркін токтың түрі (9.26) көріністік (түбір астындағы) таңбасына тәуелді.
