Элементы механики жидкости

• Гидростатическое давление столба жидкости

,

где - плотность жидкости, - ускорение свободного падения,

- высота столба жидкости.

• Сила Архимеда (выталкивающая сила, действующая на тело, погруженное в жидкость)

,

где 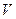- объём тела (объём жидкости, вытесненной телом).

• Уравнение неразрывности струи

,

где и - площади поперечного сечения трубки тока в двух местах, и - соответствующие скорости течений.

• Уравнение Бернулли для стационарного течения идеальной жидкости

,

где и - статические давления в двух сечениях трубки, и - высоты сечений над некоторым уровнем, и - динамические давления жидкости в этих же сечениях, и - гидростатические давления.

• Скорость истечения жидкости в открытом сосуде из малого отверстия

.

• Формула Стокса (сила сопротивления, действующая на шарик, равномерно движущийся в вязкой среде)

,

где - коэффициент динамической вязкости жидкости, - радиус шарика,

- скорость движения шарика.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Контрольная работа №1

Задача 1. Зависимость пройденного пути от времени задается уравнением

( ). Определить через сколько времени после начала движения ускорение тела станет равным 2,8 .

Дано: Решение

По определению ускорение – это производная скорости

по времени , а скорость – производная пути

по времени , поэтому выражение для скорости

запишется .

Ускорение .

_________________ Вычисления

По условию , тогда

, , откуда .

Ответ: .

Задача 2. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением , где

. Определить полное ускорение точки на ободе диска к концу второй секунды после начала движения, если линейная скорость этой точки в этот момент равна 0,4м/с.

Дано: Решение

По определению полное ускорение вращательного

движения определяется по формуле , где

- тангенциальное ускорение, - нормальное

ускорение. Поэтому нужно найти сначала линейную

скорость вращения диска .

______________ По определению линейная скорость , где

- угловая скорость вращения, которая определяется

как . Подставив выражение для угла поворота, найдем

. Тогда линейная скорость . Откуда .

Тангенциальное ускорение .

Нормальное ускорение

. Полное ускорение .

Проверяем размерностьполученного выражения для ускорения:

.

Вычисления

Ответ: .

Задача 3. Поезд массой 1200т движется со скоростью , и при торможении останавливается, пройдя путь . Найти силу торможения.

Дано: Решение

__________________

Поезд считаем материальной точкой.

На поезд действуют 3 силы: - сила тяжести,

- сила реакции опоры, - тормозящая сила, направленная противоположно направлению движения.

Согласно второму закону Ньютона (1).

Движение происходит по оси ОХ. Проецируем уравнение (1) на ось ОХ:

ОХ: , (2).

Чтобы определить , нужно выразить ускорение .

Движение поезда равнозамедленное.

По определению для равнозамедленного движения:

скорость , пройденный путь (3)

Так как поезд останавливается, то конечная скорость 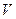равна нулю, т.е.

, откуда выражаем время движения (4). Подставляем (4)

в выражение (3) : , откуда (5).

Находим тормозящую силу, подставив (5) в (2)

(6).

Проверяем размерность конечной формулы (6)

.

Вычисления

Ответ: .

Задача 4. Маховик в виде диска массой и радиусом свободно вращается вокруг оси, проходящей через его центр, с частотой

. При торможении маховик останавливается через . Определить тормозящий момент .

Дано: Решение

диск Тормозящий момент находим из основного уравнения

динамики вращательного движения

(1), где - момент инерции диска,

- угловое ускорение вращения.

______________ Момент инерции для диска (согласно таблице) (2).

-? Угловое ускорение по определению , -

-угловая скорость, т.е. (3).

Подставляя (2) и (3) в уравнение (1), для тормозящего момента получаем:

(4).

Проверяем размерность (4)

.

Вычисления

Ответ:

Задача 5.Платформа в виде диска радиусом вращается по инерции с частотой . На краю платформы стоит человек, масса которого . С какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы . Момент инерции человека рассчитывать как для материальной точки.

Дано:

;

;

;

_________________

Решение.

Человек вместе с платформой составляет замкнутую механическую систему, поэтому момент импульса этой системы должен иметь постоянное значение.

Момент импульса системы в первом случае, когда человек стоял на краю платформы

, (1)

где - угловая скорость вращения платформы и человека в первом случае, - момент инерции человека, - момент инерции платформы.

Момент инерции человека можно определить по формуле:

.

Когда человек перейдет в центр платформы, момент инерции человека станет равным нулю (расстояние до оси вращения ), следовательно, во втором случае момент импульса человека станет равным нулю.

Момент импульса системы во втором случае

,

где - угловая скорость вращения платформы во втором случае.

Запишем закон сохранения импульса:

;

;

;

;

Производим проверку размерности расчетной формулы:

.

Вычисление:

.

Ответ: если человек перейдет в центр платформы, платформа будет вращаться с частотой равной .

Задача 6. На нити длиной 1м висит шар радиусом 5 см, опирающийся на вертикальную стенку. Нить образует со стенкой угол 30 и касается шара в очке С. Определить коэффициент трения шара о стенку.

Дано: Решение

______________

На шар действуют силы: - сила тяжести,

- сила реакции опоры, - сила натяжения нити, - сила трения. Записываем первое условие равновесия (геометрическая сумма всех сил равна нулю) : (1).

Проецируем уравнение (1) на оси ОХ и ОУ

ОХ: (2),

ОУ: (3).

Записываем для шара относительно точки С второе условие равновесия (алгебраическая сумма моментов сил равна нулю).

, (4)

где , , - моменты сил, - плечо силы трения, - плечо силы тяжести, - плечо силы реакции опоры. С учетом этих выражений уравнение (4) запишется

, (5)

Известно, что , т.е. (5) можно записать как

(6).

Решая систему уравнений (2), (3) и (6), получим для коэффициента трения

. (7)

Проверяем размерность (7)

.

Вычисления

.

Ответ: .

Задача 7. Верхний конец стержня закреплён, а к нижнему подвешен груз

. Длина стержня 6м, поперечное сечение . Определить напряжение материала стержня, его абсолютное и относительное удлинение, если модуль Юнга .

Дано: Решение

Под действием груза стержень растягивается

и в материале стержня возникает напряжение, которое

можно рассчитать по формуле . В нашем случае

_______________ , т.е. (1).

Так как деформации стержня малы, то выражение

закона Гука имеет вид: , (2)

где - относительное удлинение. Из (2) выражаем относительное удлинение . (3)

Абсолютное удлинение . (4)

Проверяем размерность (3) и (4)

(безразмерная величина), .

Вычисления

,

Ответ: , .

Задача 8. Шар массой 200г, движущийся со скоростью 10м/с, ударяет неподвижный шар массой 0,8кг. Удар прямой, центральный, абсолютно неупругий. Определить скорости шаров после удара.

Дано: Решение

кг Применяем закон сохранения импульса для абсолютно

м/с неупругого удара. После удара шары будут двигаться

кг вместе с одинаковой скоростью .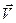

м/с . (1)

______________ Проецируем уравнение (1) на ось Х, учитывая то, что

V-? :

ОХ: , откуда найдем скорость шаров после

удара . (2)

Проверяем размерностьформулы (2)

.

Вычисления

(м/с).

Ответ: м/с.

Задача 9. В сосуд заливается вода со скоростью 0,5л/с. Пренебрегая вязкостью воды, определить диаметр отверстия в сосуде, при котором вода поддерживалась бы на постоянном уровне h = 20см.

Дано: Решение

Объём воды, выливающейся через отверстие в

сосуде определяется как

(1), где (2)- площадь

___________________

основания отверстия, - скорость истечения воды.

По формуле Торричелли скорость истечения жидкости из отверстия

равна . (3)

Подставляем (2) и (3) в уравнение (1), получаем выражение , , откуда диаметр отверстия (4)

Проверяем размерность (4)

.

Вычисления

.

Ответ: .

ЗАДАЧИ

100. Тело движется по закону . Построить графики зависимостей координаты, скорости и ускорения тела от времени. Найти координату и скорость тела через 2 с и 5 с.

101. Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением s = сt³ , где с=0,1 см/с³. Найти нормальное a_n и тангенциальное а_t ускорение точки в момент, когда линейная скорость точки V = 0,3 м/с.

102. С какой высоты падало тело, если за последние 2 с оно прошло 60 м? Сколько времени падало тело? Принять g = 10 м/с .

103. Вал вращается с частотой n = 180 об/мин. С некоторого момента вал начал вращаться равнозамедленно с угловым ускорением ε = 3 рад/с² . Через какое время t вал остановится? Найти число оборотов вала n до остановки.

104. Камень брошен под углом 30 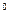к горизонту со скоростью 10 м/с. Через сколько времени он достигнет высоты 1,05 м?

105. По дуге окружности радиусом R= 10 м движется точка. В некоторый момент времени нормальное ускорение точки =4,9 м/с ; в этот момент времени векторы полного и нормального ускорений образуют угол . Найти скорость и тангенциальное ускорение .

106. Движения двух материальных точек выражаются уравнениями , где

.В какой момент времени скорости этих точек будут одинаковы? Определить скорости и , ускорения и точек в этот момент времени.

107. Модуль линейной скорости точки, лежащей на ободе вращающегося колеса, в 2,5 раза больше линейной скорости точки, лежащей на 0,05 м ближе к оси колеса. Найти радиус колеса.

108. Автобус движется по прямолинейному участку, имея скорость 15 м/с. На каком расстоянии от остановки он должен начать тормозить, если ускорение при этом не должно превышать 0,5 м/с . Сколько времени займёт торможение до полной остановки?

109. Тело, брошенное под углом 45 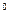к горизонту, через 5 с после бросания имело вертикальную составляющую скорости 9,8 м/с. Какова дальность полёта по горизонтали? Сопротивление воздуха не учитывать.

110. Самосвал с грузом общей массой 10 т движется по горизонтальному участку дороги со скоростью 72 км/ч. На каком расстоянии от места разгрузки самосвал должен начать тормозить, если сила торможения равна

5 кН? Сколько времени займет торможение?

111. Стальная проволока выдерживает груз, масса которого не превышает

600 кг. С каким максимальным ускорением можно поднимать груз массой 500 кг, чтобы проволока не оборвалась?

112. Радиус Земли в n = 3,66 раза больше радиуса луны; средняя плотность Земли в k = 1,66 раза больше плотности Луны. Определить ускорение свободного падения на поверхности Луны, если на поверхности Земли ускорение g = 9,81 м/с .

113. К вертикальной проволоке длиной 5 м и площадью поперечного сечения 2 мм подвешен груз массой 5,1 кг. В результате проволока удлинилась на

Х = 0,6 мм. Найти модуль Юнга Е материала проволоки.

114. В технике коэффициентом тяги автомобиля называется отношение силы тяги к силе тяжести автомобиля. С каким ускорением движется автомобиль при коэффициенте сопротивления 0,06 и коэффициенте тяги 0,11?

115. На концах невесомой и нерастяжимой нити, перекинутой через неподвижный блок, подвешены грузы, массы которых 0,6 кг и 0,4 кг. Определить какой скорости достигнут грузы через 2 с после того, как система будет предоставлена самой себе. Трением в блоке пренебречь.

116. К стальному стержню длиной 3 м и диаметром d = 2 см подвешен груз массой 2,5 т. Определить напряжение σ в стержне, относительное ε и абсолютное Δl удлинение стержня.

117. Во сколько раз уменьшится сила притяжения к Земле космического корабля при его удалении от поверхности Земли на расстояние, равное пяти радиусам земли?

118. Воздушный шар массой 160 кг опускается с постоянной скоростью. Какое количество балласта нужно выбросить, чтобы шар поднимался с той же скоростью? Подъёмная сила воздушного шара равна 1372 Н.

119. Ребёнок массой 50 кг качается на качелях, длина подвеса которых равна 4 м. С какой силой он давит на сиденье при прохождении среднего положения с линейной скоростью, равной 6 м/с?

120. На горизонтальную ось насажены маховик и легкий шкив радиусом

5 см. На шкив намотан шнур, к которому привязан груз массой 0,4 кг. Опускаясь равноускоренно груз прошел путь 1,8 м за 3 с. Определить момент инерции маховика. Массу шкива считать пренебрежимо малой. Маховик считать однородным диском.

121. Кинетическая энергия вращающегося маховика равна 1000 Дж. Под действием постоянного вращающего момента маховик начал вращаться равнозамедленно и, сделав 80 оборотов, остановился. Определить момент силы торможения. Маховик считать однородным диском.

122. Поезд массой 2000 т идет по горизонтальному участку пути с постоянной скоростью 10 м/с. Коэффициент трения равен 0,05. Какую мощность развивает тепловоз на этом участке?

123. Пуля, летящая со скоростью 400 м/с, попадает в земляной вал и проходит до остановки 0,5 м. Определить силу сопротивления движению пули, если её масса 24 г.

124. Если к телу приложить силу F = 130 Н под углом α = 60° к горизонту, то тело будет двигаться равномерно. С каким ускорением а будет двигаться тело, если приложить ту же силу под углом β = 30° к горизонту. Масса тела m = 25 кг ?

125. Маховик, момент инерции которого равен 40 кг·м , начал вращаться равноускоренно из состояния покоя под действием момента силы, равного

20 Н·м. Равноускоренное вращение продолжалось 10 с. Определить кинетическую энергию, приобретённую маховиком. Маховик считать однородным диском.

126. Какую работу совершает человек, поднимающий груз массой 2 кг на высоту 1,5 м с ускорением 3 м/с ?

127. Моторы электровоза при движении со средней скоростью 20 м/с потребляют мощность 8·10 Вт. Какова сила тяги мотора, если коэффициент полезного действия силовой установки электровоза 80%.

128. На барабан массой m = 12 кг намотан шнур, к концу которого привязан груз массой m = 3 кг. Найти ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь.

129. Якорь мотора делает 1500 об/мин. Определить вращающий момент, если мотор развивает мощность 500 Вт.

130. Концы стержня массой 0,1·10 кг и длиной 0,4 м нагружены сосредоточенными массами 0,4·10 кг и 0,1·10 кг. Где следует закрепить стержень, чтобы он находился в положении статического равновесия?

131. Однородная балка массой 50 кг лежит на двух опорах. На расстоянии четверти длины балки от левой опоры она нагружена сосредоточенной массой 100 кг. Найти модули сил давления балки на опоры, равные по модулю.

132. Лодку тянут к берегу двумя канатами, расположенными в горизонтальной плоскости. Угол между канатами 90 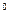. К канатам приложены силы 1,2·10 Н каждая. Какой по модулю должна быть сила сопротивления воды, чтобы лодка, приближаясь к берегу, находилась в положении статического равновесия?

133. Найти силы, действующие на стержни АВ и АС (рис.1), если α = 60 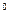, а масса лампы 3 кг.

Рис.1

134. К концу стержня АС (рис. 2) длиной 2 м, укреплённого шарнирно одним концом к стене, а с другого конца, поддерживаемого тросом ВС длиной 2,5 м, подвешен груз массой 120 кг. Найти силы, действующие на трос и стержень.

Рис. 2

135. Электрическая лампа (рис.3) подвешена на шнуре и оттянута горизонтальной оттяжкой. Найти силу натяжения шнура АВ и оттяжки ВС, если масса лампы 1 кг, а угол α = 60 .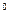

Рис. 3

136. Двое рабочих переносят цилиндрическую трубу массой 80 кг. Один из них поддерживает трубу на расстоянии 1 м от конца, а второй поддерживает противоположный её конец. Определить модуль нагрузки, приходящийся на каждого рабочего, если длина трубы равна 5 м.

137.Под каким наименьшим углом к горизонту можно прислонить лестницу к гладкой вертикальной стене, если коэффициент трения лестницы о пол и о стену равен 0,4? Считать, что центр тяжести лестницы находится в её середине.

138. На нити, прикреплённой одним концом к вертикальной стене, висит шар, опирающийся на эту стену. Длина нити 0,8 м, радиус шара 12 см. Нить касается шара и образует с плоскостью стены угол α = 30 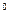. Найти коэффициент трения шара о стену.

139. Найти давление в морской воде на глубине 8,5 м. Атмосферное давление равно 1,01·10 Па. Плотность морской воды 1,03·10 кг/м .

140. При забивании сваи массой 150 кг использовалась энергия свободно падающего молота массой 50 кг. При этом свая погружалась в грунт на 10 см. С какой высоты должен падать молот, если сила сопротивления грунта постоянна и равна 6850 Н? Удар считать неупругим.

141. Вагон массой 20 т, двигаясь со скоростью 0,5 м/с, ударяется в два неподвижных пружинных буфера. Найти максимальное сжатие буферов, если известно, что при действии на каждый буфер силы 50 кН он сжимается на 1 см.

142. Два абсолютно упругих шара массами 10 г и 20 г движутся навстречу друг другу со скоростями соответственно 20 м/с и 10 м/с по идеально гладкой горизонтальной поверхности. Найти скорости шаров после абсолютно упругого удара.

143. На краю горизонтальной платформы, имеющей форму диска радиусом R = 2м, стоит человек массой m = 80 кг. Масса платформы равна 240 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через её центр. Пренебрегая трением, найти, с какой угловой скоростью ω будет вращаться платформа, если человек будет идти вдоль её края со скоростью

2 м/с относительно платформы.

144. Горизонтальная платформа массой m = 120 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой ν = 20 об/мин. Человек массой m = 80 кг стоит при этом на краю платформы. С какой частотой ν начнёт вращаться платформа, если человек перейдёт от её края к центру платформы? Считать платформу однородным диском, а человека – точечной массой.

145. Для определения скорости пули используют баллистический маятник. С какой по модулю горизонтальной скоростью летела пуля массой 10 г, если маятник массой 5 кг, подвешенный на нити длиной 4 м, после попадания в него пули отклонился на угол 25 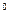от вертикали?

146. Платформа, имеющая форму сплошного однородного диска, вращается по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдёт ближе к центру на расстояние, равное половине радиуса платформы.

147. При центральном упругом ударе движущееся тело массой m ударяется о покоящееся тело массой m , в результате чего скорость первого уменьшается в 3 раза. Определить: 1) во сколько раз масса первого тела больше массы второго тела; 2) кинетическую энергию второго тела непосредственно после удара, если первоначальная кинетическая энергия первого тела равна 900 Дж.

148. Человек стоит на скамье Жуковского и ловит рукой мяч массой 0,4 кг, летящий в горизонтальном направлении со скоростью 20 м/с. Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнёт вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6 кг·м .

149. Шар массой m = 1,8 кг сталкивается с покоящимся шаром большей массы М. В результате прямого упругого удара шар потерял w = ¾ своей кинетической энергии. Определить массу большего шара.

150. Определите радиус r трубы, по которой со скоростью 0,3 м/с течёт углекислый газ (ρ =7,5 кг/м ). Если за 20 мин через поперечное сечение трубы протекает m = 1,4 кг газа.

151. В сосуд заливается вода со скоростью 0,6 л/с. Пренебрегая вязкостью воды, определить диаметр отверстия в сосуде, при котором вода поддерживалась бы в нём на постоянном уровне h = 9 см.

152. В дне сосуда имеется отверстие диаметром d = 2 см. В сосуде вода поддерживается на постоянном уровне h = 80 см. Считая, что струя не разбрызгивается, и пренебрегая силами трения в жидкости, определить диаметр струи, вытекающей из сосуда на расстоянии h = 2h от его дна.

153. Какой диаметр d должен иметь стальной трос подъёмного крана, если максимальная масса поднимаемого груза m= 10 т? Предел прочности стали σ_п = 500 МПа. Запас прочности должен быть равен k = 6.

154. Бак высотой h = 1,5 м наполнен до краев водой. На расстоянии d = 1 м от верхнего края бака образовалось отверстие малого диаметра. На каком расстоянии от бака падает на пол струя, вытекающая из отверстия?

155. В широкой части горизонтально расположенной трубы нефть течёт со скоростью = 2 м/с. Определить скорость нефти в узкой части трубы, если разность давлений в широкой и узкой частях её равна 6,65 кПа. Плотность нефти равна ρ = 900 кг/м³.

156. Струя воды, движущаяся со скоростью = 10 м/с, ударяется о неподвижную плоскую поверхность, поставленную перпендикулярно струе. Найти силу давления струи на поверхность, считая, что после удара о поверхность скорость частиц воды равна нулю.

157. Разность давлений в широком и узком ( =10 см, = 4 см) коленах горизонтальной трубы составляет 120 Па. Определить с какой скоростью продувается воздух (ρ = 1,29 кг/м ) в широком колене.

158. Определите, на какую высоту h поднимется вода в вертикальной трубке, впаянной в узкую часть горизонтальной трубы диаметром = 3 см, если в широкой части трубы диаметром = 9 см со скоростью газа = 25 см/с.

159. На столе стоит наполненный водой широкий цилиндрический сосуд высотой h = 40 см. пренебрегая вязкостью, определить, на какой высоте от дна сосуда должно располагаться небольшое отверстие, чтобы расстояние по горизонтали от отверстия до места, куда попадает струя воды, было максимальным.

ОСНОВНЫЕ ФОРМУЛЫ

КОНТРОЛЬНАЯ № 2

Электростатика

•Закон Кулона

,

где - сила взаимодействия двух точечных зарядов 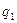и 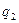, находящихся на расстоянии 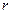друг от друга; - электрическая постоянная,

-диэлектрическая проницаемость среды (для воздуха );

•Напряженность электрического поля, создаваемого зарядом

, ;

где - положительный точечный заряд, помещенный в точку поля, в которой определяют напряжённость.

• Принцип суперпозиции электрических полей

;

В случае двух полей , 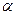-угол между ;

• Поток вектора напряжённости через замкнутую поверхность

;

где - проекция вектора напряженности на нормаль к поверхности, - элемент поверхности.

• Теорема Гаусса.

Поток вектора напряжённости через замкнутую поверхность, охватывающую заряды равен

;

• Потенциал электрического поля

, , ,

где - потенциальная энергия электрического поля; А- работа по перемещению положительного точечного заряда из данной точки в бесконечность;

• Работа поля по перемещению заряда из одной точки поля в другую

;

• Для однородного электрического поля

,

где - расстояние между эквипотенциальными поверхностями.