Удар по вращающемуся телу
При исследовании удара по вращающемуся телу кроме теоремы об изменении количества движения приходится использовать и закон моментов. Относительно оси вращения его запишем так 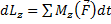 и, после интегрирования за время удара
и, после интегрирования за время удара 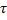 ,
, 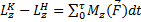 или
или 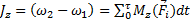 где
где 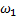 и
и 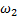 - угловые скорости тела в начале и в конце удара,
- угловые скорости тела в начале и в конце удара, 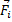 - ударные силы.
- ударные силы.
Правую часть надо немного преобразовать. Найдем, сначала, интеграл момента ударной силы относительно неподвижной точки О:
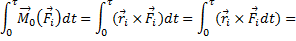
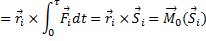
При этом предполагалось, что за малое время удара τ радиус-вектор 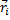 считался неизменным, постоянным.
считался неизменным, постоянным.
Проектируя результат этого векторного равенства на ось вращения z, проходящую через точку О, получим 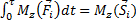 , т.е. интеграл равен моменту вектора импульса ударной силы относительно оси вращения. Закон моментов в преобразованном виде запишется, теперь, так:
, т.е. интеграл равен моменту вектора импульса ударной силы относительно оси вращения. Закон моментов в преобразованном виде запишется, теперь, так:
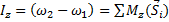 . (10)
. (10)
В качестве примера рассмотрим удар вращающегося тела о неподвижную преграду.
Тело, вращаясь вокруг горизонтальной оси О, ударяется о преграду А (рис.8). Определим ударные импульсы сил, возникающих в подшипниках на оси, 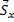 и
и 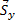 .
.
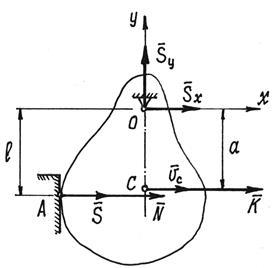
Рис.8
По теореме об изменении количества движения 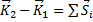 в проекциях на оси х и у получим два уравнения:
в проекциях на оси х и у получим два уравнения:
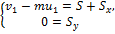
где скорости центра масс С в начале и конце удара 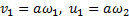 Поэтому первое уравнение станет таким
Поэтому первое уравнение станет таким 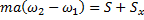 .
.
Третье уравнение, по (10), получится в виде 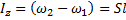 из которого находим
из которого находим 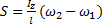 .
.
И, так как коэффициент восстановления
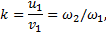
то 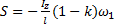 (в нашем примере
(в нашем примере 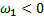 , поэтому ударный импульс S > 0, то есть направлен так, как показано на рисунке).
, поэтому ударный импульс S > 0, то есть направлен так, как показано на рисунке).
Находим импульсы реакции оси: 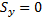
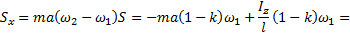
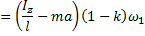
Обязательно надо обратить внимание на то, что при 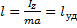 ударные импульсы в подшипниках оси будут равны нулю.
ударные импульсы в подшипниках оси будут равны нулю.
Место, точка удара, расположенная на этом расстоянии 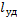 от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках не возникают.
от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках не возникают.
Кстати, заметим, что центр удара совпадает с точкой где приложены равнодействующая сил инерции и вектор количества движения.
Вспомним, что при ударе длинной палкой по неподвижному предмету, мы нередко испытывали рукой неприятный ударный импульс, как говорят – «отбивали руку».
Нетрудно найти в этом случае центр удара – место, которым следует ударить, чтобы не почувствовать это неприятное ощущение (рис.9).
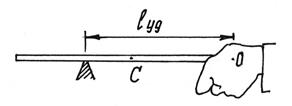
Рис.9
Так как 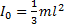 (l – длина палки) и a=OC=0,5l то
(l – длина палки) и a=OC=0,5l то
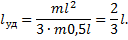
Следовательно, центр удара находится на расстоянии трети длины от конца палки.
Понятие центра удара учитывают при создании различных ударных механизмов и других конструкций, где встречаются ударные процессы.
Пример 12. Стержень массы m2 и длины l, который может свободно вращаться вокруг неподвижной горизонтальной оси, проходящей через один из его концов, под действием силы тяжести переходит из горизонтального положения в вертикальное. Проходя через вертикальное положение, нижний конец стержня ударяет о небольшой кубик массы m1, лежащий на горизонтальном столе. Определить:
а) на какое расстояние переместится кубик m1, если коэффициент трения о поверхность стола равен μ;
б) на какой угол отклонится стержень после удара.
Рассмотреть случаи абсолютно упругого и неупругого ударов.

Рис.10
Решение. В задаче описывается несколько процессов: падение стержня, удар, движение кубика, подъем стержня. Рассмотрим каждый из процессов.
Падение стержня.На стержень действует потенциальная сила тяжести и сила реакции оси, которая работы при вращательном движении стержня не совершает, т.к. момент этой силы равен нулю. Следовательно, выполняется закон сохранения энергии.
В начальном горизонтальном состоянии стержень обладал потенциальной энергией
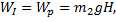
где h - высота подъема центра масс стержня H=l/2,
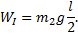
В конечном вертикальном состоянии (до удара) стержень обладал кинетической энергией вращательного движения
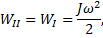
где J - момент инерции стержня относительно оси, проходящей через его конец:
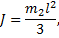
ω - угловая скорость. Следовательно,
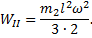
По закону сохранения энергии WI=WII получаем:
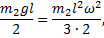
откуда угловая скорость стержня до удара равна

Процесс удара.Система состоит из двух тел - стержня и кубика. Рассмотрим случаи неупругого и упругого ударов.
Неупругий удар. При ударе материальных точек или твердых тел, движущихся поступательно, выполняется закон сохранения импульса. Если хотя бы одно из взаимодействующих тел совершает вращательное движение, то следует применять закон сохранения момента импульса. При неупругом ударе оба тела после удара начинают движение с одной и той же угловой скоростью, скорость кубика совпадает с линейной скоростью нижнего конца стержня.
До удара (состояние II) двигался только стержень, его момент импульса относительно оси, проходящей через точку подвеса, равен:
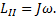
После удара (состояние III) движутся стержень и кубик с одинаковой угловой скоростью ω3. Их момент импульса равен
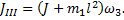
Здесь 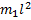 - момент инерции кубика (материальной точки) относительно рассматриваемой оси.
- момент инерции кубика (материальной точки) относительно рассматриваемой оси.
По закону сохранения момента импульса LII=LIII имеем
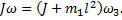
Откуда
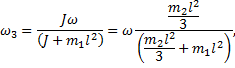
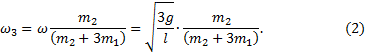
Линейная скорость кубика равна
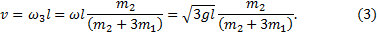
Упругий удар. После абсолютно упруго удара оба тела движутся по отдельности. Кубик движется со скоростью v, стержень - с угловой скоростью ω3. Кроме закона сохранения момента импульса для этой системы тел выполняется закон сохранения энергии.
До удара (состояние II) двигался только стержень, его момент импульса относительно оси, проходящей через точку подвеса, равен
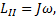
а кинетическая энергия определяется выражением
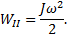
После удара (состояние III) момент импульса стержня 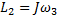 , момент импульса кубика (материальной точки
, момент импульса кубика (материальной точки 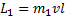 , поэтому суммарный момент импульса системы
, поэтому суммарный момент импульса системы
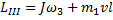
Кинетическая энергия вращательного движения стержня составит 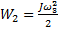 , а кинетическая энергия кубика
, а кинетическая энергия кубика 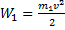 , поэтому полная энергия системы равна
, поэтому полная энергия системы равна
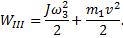
Применим законы сохранения энергии WII=WIII и момента импульса LII=LIII:
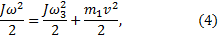
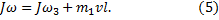
Получили систему двух уравнений с двумя неизвестными. Преобразуем ее к виду:
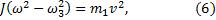
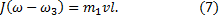
Разделим (6) на (7) и учтем, что 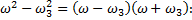

Подставляя 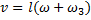 в уравнение (7)
в уравнение (7)
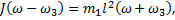
получим выражение для угловой скорости стержня.
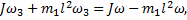
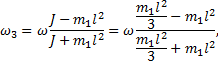
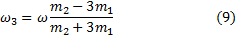
Скорость кубика
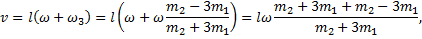
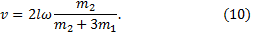
Подъем стержня (рис.11).Этот процесс, также как и первый, описывается законом сохранения энергии.

Рис.11
Кинетическая энергия стержня 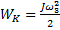 превращается в его потенциальную энергию
превращается в его потенциальную энергию 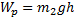 , то есть
, то есть
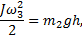
откуда высота подъема центра масс стержня
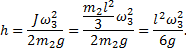
Определим угол отклонения стержня. Проведем расчет только для неупругого удара. Из рисунка видно, что
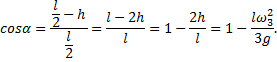
Подставим формулу (2) в последнее выражение:
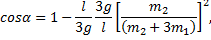
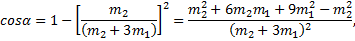
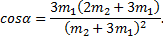
Движение кубика.В процессе движения на кубик действуют сила тяжести m1g, сила нормального давления N и сила трения скольжения 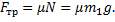 Кинетическая энергия кубика уменьшается до нуля вследствие того, что сила трения совершает работу. Следовательно, по теореме о кинетической энергии
Кинетическая энергия кубика уменьшается до нуля вследствие того, что сила трения совершает работу. Следовательно, по теореме о кинетической энергии
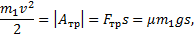
откуда перемещение кубика составит
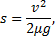
где скорость при неупругом ударе определяется выражением (3).
Вопросы для самопроверки
- Какое явление называется ударом?
- Чем характеризуется ударная сила?
- Какой эффект имеет действие ударной силы на материальную точку?
- Сформулируйте теорему об изменении количества движения механической системы при ударе в векторной форме и в проекциях на оси координат.
- Могут ли внутренние ударные импульсы изменить количество движения механической системы?
- Что называют коэффициентом восстановления при ударе и как он определяется опытным путем? В каких пределах находятся его числовые значения?
- Какова зависимость между углами падения и отражения при ударе о гладкую неподвижную поверхность?
- Чем характеризуются первая и вторая фазы упругого удара? В чем состоит особенность абсолютно упругого удара?
- Как определяются скорости двух шаров в конце каждой фазы прямого центрального удара (неупругого, упругого, абсолютно упругого)?
- Какова зависимость между ударными импульсами второй и первой фаз при абсолютно упругом ударе?
- Какова потеря кинетической энергии двух соударяющихся тел при неупругом, упругом и абсолютно упругом ударах?
- Как формулируется теорема Карно?
- Как формулируется теорема об изменении кинетического момента механической системы при ударе в векторной форме и в проекциях на оси координат?
- Могут ли внутренние ударные импульсы изменить кинетический момент механической системы?
- Какие изменения вносит действие ударных сил в движение твердых тел: вращающегося вокруг неподвижной оси и совершающего плоское движение?
- При каких условиях опоры вращающегося тела не испытывают действия внешнего ударного импульса, приложенного к телу?
- Что называют центром удара и каковы его координаты?
