Параметрические цепи

Преобразование частоты

Радиотехнические цепи, один или несколько параметров которых изменяются во времени по заданному закону, называют параметрическими(линейными цепями с переменными параметрами). Предполагается, что изменение какого-либо параметра осуществляют электронным методом с помощью управляющего сигнала. В линейно-параметрической цепи параметры элементов не зависят от уровня сигнала, но могут независимо изменяться во времени. Реально параметрический элемент получают из нелинейного элемента, на вход которого подают сумму двух независимых сигналов. Один из них несет информацию и имеет малую амплитуду, так что в области его изменений параметры цепи практически постоянны. Вторым является управляющий сигнал большой амплитуды, который изменяет положение рабочей точки нелинейного элемента, а следовательно, его параметр.

Преобразование частоты в радиотехнике осуществляется параметрическими цепями. В таких цепях один или несколько параметров изменяются во времени по заданному закону. При этом предполагается, что изменение (точнее, модуляция) осуществляется электронным методом с помощью управляющего сигнала. В радиотехнике широко применяются параметрические сопротивления 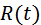, индуктивности 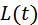и ёмкости .

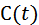Важная роль, отводимая в радиотехнике параметрическим цепям, обусловлена их способностью преобразовывать спектры входных сигналов, а также возможностью создания малошумящих параметрических усилителей.

Чаще всего в качестве параметрической цепи применяются параметрические сопротивления 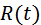. На практике параметрически управляемые резисторы создают следующим образом. На вход безынерционного нелинейного двухполюсника с вольт-амперной характеристикой 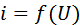подают сумму двух колебаний: управляющего напряжения 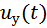и напряжения сигнала 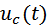. При этом управляющее напряжение должно значительно превышать по амплитуде полезный сигнал (рис.1).

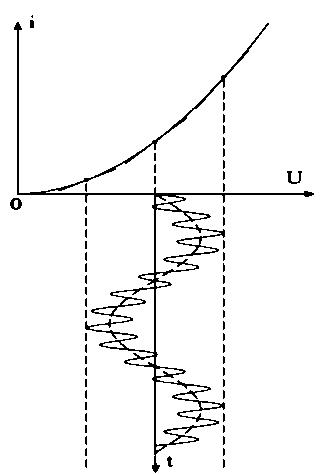
Рис.1. Принцип работы параметрической цепи

Преобразованием частоты называется трансформация модулированного сигнала, связанная с переносом его спектра из области несущей частоты 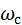в область некоторой промежуточной частоты 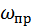, совершаемая без изменения закона модуляции. Преобразователь частоты(ПрЧ) состоит из смесителя – параметрического безынерционного элемента, и гетеродина – вспомогательного генератора гармонических колебаний с частотой 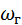, служащего для параметрического управления смесителем. Под действием напряжения гетеродина дифференциальная крутизна вольт-амперной характеристики смесителя периодически изменяется во времени.

Здесь необходимо дать определение дифференциальной крутизны ВАХ.

Преобразование частоты, как уже было сказано, происходит на основе безынерционного параметрического элемента, в качестве которого чаще всего используется кристаллический диод. По характеру ВАХ кристаллический диод представляет собой нелинейный двухполюсник. Понятие сопротивления для нелинейного двухполюсника можно определить по-разному. Пусть ВАХ этого двухполюсника описывается в общем случае выражением 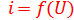. Приложив к двухполюснику постоянное напряжение 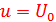, будем иметь ток в цепи 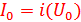. Отношение 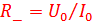называют сопротивлением элемента постоянному току. В отличие от обычного сопротивления линейного резистора значение величины 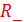не постоянно и зависит от приложенного напряжения.

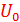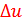Часто приходится иметь дело с одновременным воздействием на нелинейный элемент двух источников напряжения: и , причём 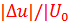| 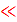1. (Именно так и работает преобразователь частоты).Разложив ВАХ в ряд Тейлора в окрестности точки 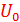, находим ток

.

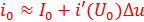Отношение приращения напряжения к приращению тока в выбранной рабочей точке ( 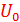, 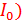называют дифференциальным сопротивлением двухполюсника:

.

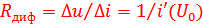Иногда удобнее пользоваться дифференциальной крутизной ВАХ, которая является тангенсом угла наклона касательной ВАХ в данной рабочей точке (рис.2):

.

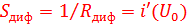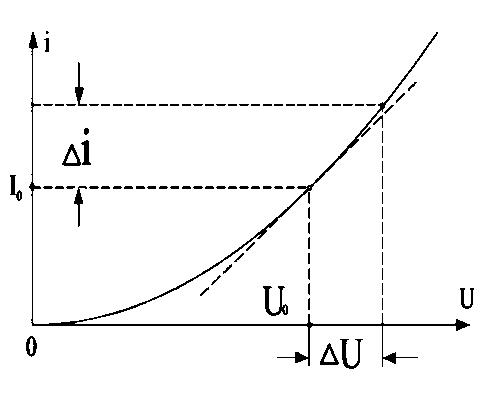
Рис.2. К определению дифференциального сопротивления и крутизны ВАХ

Необходимо подчеркнуть, что, вводя понятие дифференциального сопротивления или дифференциальной крутизны, мы, по сути дела, производим линеаризацию реальной ВАХ, что справедливо лишь для малых приращений сигнала относительно рабочей точки.

Примером одного из параметрических сопротивлений может служить обычный кристаллический диод с нелинейной (обычно квадратичной) характеристикой, на вход которого подаётся управляющее (гетеродинное) переменное напряжение 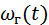.В этом случае крутизна его вольт-амперной характеристики будет изменяться во времени и будет связана с управляющим напряжением функциональной зависимостью 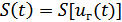. Если на этот же диод подать ещё и напряжение модулированного сигнала 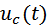, то его результирующий ток определится выражением:

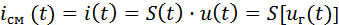....................... (1).

Поскольку параметрическая цепь является линейной цепью, к ней применим принцип суперпозиции. Действительно, если приложенное к цепи напряжение является суммой двух переменных

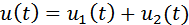, .................................(2)

то, подставив (2) в (1), получим выходной ток также в виде суммы двух составляющих

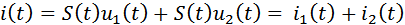............. (3)

Выражение (3) показывает, что отклик параметрической цепи на сумму двух сигналов равен сумме её откликов на каждый сигнал в отдельности.

Структурная схема преобразователя частоты показана на рис.3.

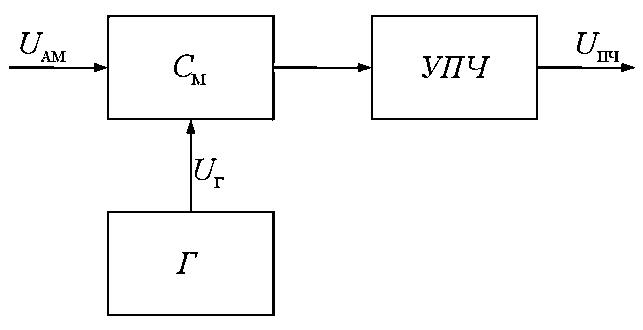
Рис.3. Структурная схема преобразователя частоты

Как видно из рис.3, преобразователь частоты состоит из смесителя (СМ) – параметрического элемента (например, кристаллического диода с квадратичной характеристикой, варикапа или МДП- транзистора), гетеродина (Г) – вспомогательного автогенератора гармонических колебаний с частотой 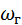, служащего для параметрического управления смесителем, и фильтра промежуточной частоты (обычно входного колебательного контура УПЧ).

Принцип действия преобразователя частоты рассмотрим на примере переноса спектра однотонального АМ- сигнала. Предположим, что под воздействием напряжения гетеродина

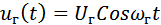................. (4)

крутизна характеристики смесительного диода изменяется во времени по закону

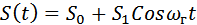,.............. (5)

где 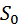и 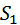– соответственно среднее значение и первая гармоническая составляющая крутизны характеристики диода.

При поступлении на смесительный диод АМ- сигнала

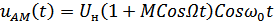
переменная составляющая выходного тока в соответствии с (1) и (5) будет определяться выражением:

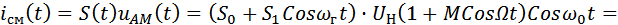
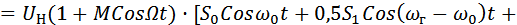
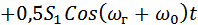……………………………(6)

Если в качестве промежуточной частоты выбрать

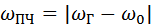. ...............(7)

то, выделив её с помощью контура УПЧ из спектра тока (6), получим преобразованный АМ- сигнал с тем же законом модуляции, но с существенно меньшей несущей частотой

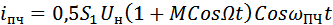............ (8)

В реальных схемах смесителей в спектре тока, кроме составляющих с частотам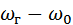и и 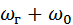, содержатся составляющие комбинационных частот

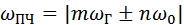,.................. (9)

где 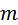и 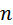– любые целые положительные числа.

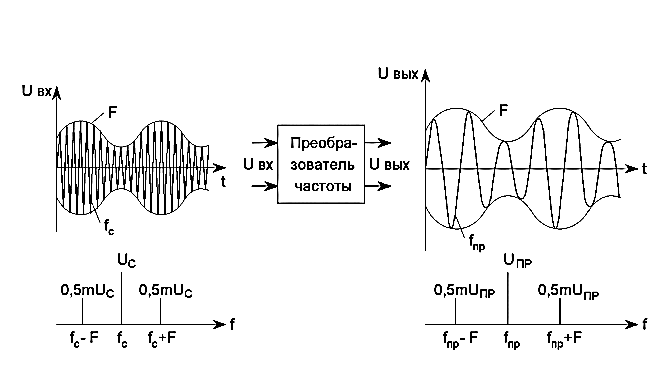
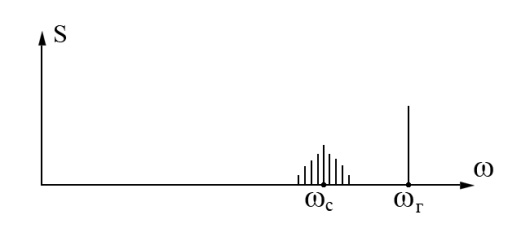
Процесс преобразования частоты показан на рис.4.

Современные преобразователи частоты с параметрическими резистивными цепями построены на принципиально новой основе. В них в качестве смесителей используются аналоговые перемножители.

а)

б)

в)

Рис.4. К объяснению процесса преобразования частоты

Если на входы аналогового перемножителя подать два гармонических колебания: некий модулированный сигнал

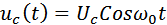.............. (10)

и опорное напряжение гетеродина

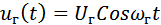, ................ (11)

то его выходное напряжение будет содержать две составляющие

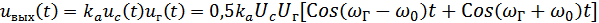
........................ (12)

Спектральная составляющая с разностной частотой 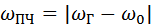выделяется узкополосным фильтром УПЧ и используется в качестве промежуточной частоты преобразованного сигнала.

Преобразование частоты широко используется в радиоприёмных устройствах (РПрУ) супергетеродинного типа. Структурная схема супергетеродинного РПрУ приведена на рис.5. Сигнал, принятый антенной, через фильтрующую входную цепь (ВЦ), защищающую приёмник от помех, действующих на «зеркальной частоте», поступает на усилитель радиочастоты (УРЧ), а с него – напреобразователь частоты (ПрЧ). С выхода преобразователя сигнал на промежуточной частоте поступает на усилитель промежуточной частоты (УПЧ), где происходит основное усиление принятого сигнала и обеспечивается защита приёмника от помех по соседнему каналу.

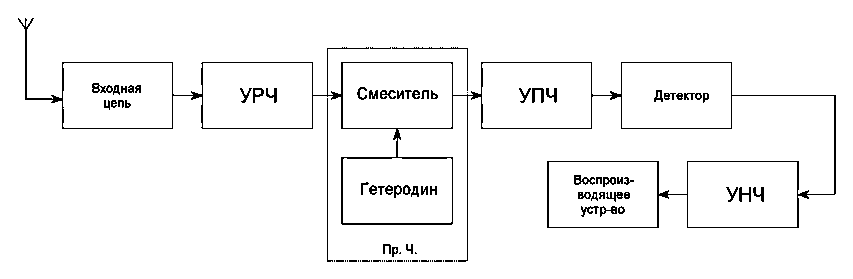
Рис.5. Структурная схема супергетеродинного радиоприёмника

Основным достоинством супергетеродинного приёмника является неизменность его промежуточной частоты, что позволяет перестраивать лишь гетеродин и входные колебательные системы.