Векторний добуток двох векторів

Означення. Векторним добутком векторів називається вектор , який задовольняє умови:

1) 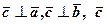- перпендикулярний площині векторів ;

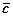2) - модуль вектора чисельно дорівнює площі паралелограма, побудованого на векторах ;

3) вектор 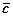напрямлений у той бік, з якого поворот від 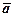до на найменший кут здійснюється проти руху стрілки годинника.

Рис. 20

Властивості векторного добутку.

Таблиця векторного множення ортів.

Векторний добуток одноіменних ортів дорівнює 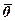. При найкоротшому повороті від одного орта до іншого проти годинникової стрілки отримуємо третій орт, за годинниковою стрілкою - третій орт із знаком « - ».

Формули векторного добутку в координатній формі отримуємо із врахуванням таблиці векторного добутку ортів

Приклад 1. Знайти векторний добуток векторів 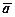=(1,3,-1) і 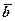=(0,2,1). Побудувати в системі координат вектори 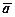, 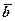і .

Розв’язання. Зауважимо, що визначник (1) зручніше обчислювати, застосувавши теорему про розклад (див. І, 1.4) за елементами першого рядка:

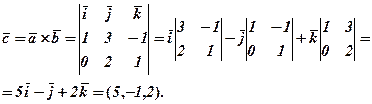
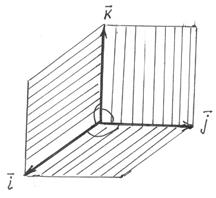
Тепер побудуємо вектори 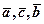за їх координатами.

З рисунка видно, що положення знайденого вектора 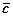відповідає означенню векторного добутку .

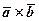Приклад 2. Знайти площу трикутника АВС, якщо

А(1,-2,-1), В(2,3,1), С(0,1,4).

Розв’язання. Знаходимо вектори

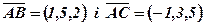і їх векторний добуток:

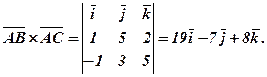
Довжина отриманого вектора за означенням чисельно дорівнює площі паралелограма, побудованого на даних векторах. Тому

.

а площа АВС складає половину знайденої площі, тобто