По какой из формул определяют величину интервала при группировке с неравными интервалами?
1. 
; 2. 
; 3. 
; 4.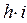 
.
4. Что можно определить по формуле: 
?
1) величину интервала при группировке с неравными интервалами; 2) величину интервала при группировке с равными интервалами и известным количеством групп; 3) величину интервала при группировке с равными интервалами и не известным количеством групп.
5. Какая таблица называется групповой?
1) содержащая группы в сказуемом; 2) содержащая в подлежащем перечень единиц совокупности; 3) содержащая в подлежащем группировку по нескольким признакам; 4) содержащая в подлежащем группировку по одному признаку.
6. Какая таблица считается комбинационной?
1) содержащая группы в сказуемом; 2) содержащая в подлежащем перечень периодов времени; 3) содержащая в подлежащем группировку по нескольким признакам; 4) содержащая в подлежащем группировку по одному признаку.
Чему будет равен интервал группировки, если минимальное значение признака равно 5, максимальное – 20 и необходимо образовать 3 группы?
1) 5; 2) 3; 3) 15; 4) 17.
Чему будет равен интервал группировки, если минимальное значение факторного признака равно 300, максимальное – 1500, объём совокупности составляет 10 единиц?
1) 600; 2) 500; 3) 100; 4) 400.
Сколько групп следует образовать, если минимальное значение группировочного признака равно 50, максимальное – 500, а интервал группировки равен 90?
1) 5; 2) 9; 3) 10; 4) 50.
Для чего служит аналитическая группировка?
1) для выделения социально-экономических типов явлений; 2) для изучения структуры совокупности; 3) для выявления взаимосвязи между явлениями.
Решение типовых задач
Пример 1.Имеются следующие данные о тарифных разрядах рабочих: 5, 4, 2, 1, 6, 3, 3, 4, 3, 2, 2, 5, 6, 4, 3, 5, 4, 1, 2, 3, 3, 4, 6, 6, 5, 1, 3, 4, 2, 5, 4, 3, 3, 4, 6, 4, 4, 3, 4, 3, 3, 4, 6, 3, 5, 4, 3, 3, 3, 4, 4, 5, 4, 3, 2, 5, 4, 2, 3, 5.
Постройте по этим данным: 1) ранжированный ряд рабочих по тарифному разряду; 2) ряд распределения рабочих по уровню квалификации: а) дискретный; б) интервальный, выделив 3 группы рабочих: низкой квалификации (1 - 2 разряды), средней квалификации (3 -4 разряды), высокой квалификации (5 - 6 разряды).
Решение
1.Для построения ранжированного ряда необходимо разряды всех рабочих распределить в порядке возрастания. Ранжированный ряд: 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6.
2. Ряд распределения рабочих по уровню квалификации:
а) дискретный:
Таблица 2.8
Дискретный ряд распределения рабочих по уровню
квалификации (разрядам)
| Разряды рабочих | Итого | ||||||
| Число рабочих, чел. |
б) интервальный ряд, образовав 3 группы рабочих по разрядам: [1 - 2], [3 - 4], [5 - 6].
Таблица 2.9
Интервальный ряд распределения рабочих по разрядам
| Группы рабочих по разрядам | Число рабочих,чел | Удельный вес рабочих,% |
| А | 1 | 2 |
| 1 - 2 | 17,0 | |
| 3 - 4 | 58,0 | |
| 5 - 6 | 25,0 | |
| Итого | 100,0 |
Интервальный ряд распределения рабочих по уровню квалификации можно построить и по атрибутивному признаку.
Таблица 2.10
Распределение рабочих по уровню квалификации
| Уровень квалификации рабочих | Число рабочих, чел | Удельный вес рабочих, % |
| А | 1 | 2 |
| Низкая (1 - 2 разр.) | 17,0 | |
| Средняя (3 - 4 разр.) | 58,0 | |
| Высокая (5 - 6 разр.) | 25,0 | |
| Итого | 100,0 |
Следовательно, наибольший удельный вес в данной совокупности занимают рабочие со средней квалификацией (58%), а наименьший – с низкой, их удельный вес составляет 17%. Данная группировка (табл. 2.10) по содержанию задачи является типологической, по характеру рассматриваемых признаков – атрибутивной, по числу группировочных признаков – простой.
Пример 2.Имеются следующие данные по 25 предприятиям обрабатывающей промышленности.
| Номер предприятия | Средняя списочная численность рабочих за отчетный год, чел. | Валовой выпуск продукции за отчетный год, млн.грн. |
| 1 | 2 | 3 |
| 1,4 | ||
| 4,8 | ||
| 3,7 | ||
| 6,1 | ||
| 9,4 | ||
| 9,6 | ||
| 2,1 | ||
| 2,6 | ||
| 4,5 | ||
| 8,4 | ||
| 9,7 | ||
| 2,3 | ||
| 3,4 | ||
| 6,3 | ||
| 9,8 | ||
| 7,3 | ||
| 1,8 | ||
| 2,6 | ||
| 4,8 |
Продолжение таблицы
| 1 | 2 | 3 |
| 16,1 | ||
| 1,3 | ||
| 2,3 | ||
| 21,3 | ||
| 2,9 | ||
| 3,4 |
1. Применяя метод аналитической группировки, выявите характер зависимости между изменением численности рабочих и выпуском продукции. При группировке по факторному признаку образуйте 4 группы с равными интервалами. 2. Выполните структурную группировку.
Решение
1. По содержанию показателей определяются факторный и результативный признаки: факторный (x) – среднесписочная численность рабочих, результативный (y) – валовой выпуск продукции.
2. Интервал группировки по факторному признаку при заданном числе групп (k = 4):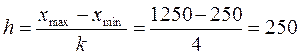 
чел.
где xmax и xmin – соответственно, максимальная и минимальная средне списочная численность рабочих, чел; k – количество групп.
Образуем следующие группы по численности рабочих, чел: [50 - 500]; [500- 750]; [750– 1000]; [1000– 1250]. Все вспомогательные расчеты целесообразно свести в таблице 2.11.
Таблица 2.11
Вспомогательные расчеты для выполнения аналитической группировки
| Группы предприятий по численности рабочих,чел | Номер пред-тия | Валовой выпуск продукции,млн.грн | Среднесписочная чис-ленность рабочих,чел | |||
| 1 | 2 | 3 | 4 | |||
| 250 - 500 | 1,4 | |||||
| 4,8 | ||||||
| 3,7 | ||||||
| 2,1 | ||||||
| 2,3 | ||||||
| 1,8 | ||||||
| 2,6 | ||||||
| 1,3 | ||||||
| Продолжение таблицы 2.11 | ||||||
| 1 | 2 | 3 | 4 | |||
| 2,3 | ||||||
| 1,3 | ||||||
| 3,4 | ||||||
 Итого | 27,0 | |||||
| 500 - 750 | 6,1 | |||||
| 9,4 | ||||||
| 2,6 | ||||||
| 4,5 | ||||||
| 3,4 | ||||||
| 6,3 | ||||||
| 7,3 | ||||||
| 4,8 | ||||||
 Итого | 44,4 | |||||
| 750 - 1000 | 8,4 | |||||
| 9,7 | ||||||
| 9,8 | ||||||
| 2,9 | ||||||
 Итого | 30,8 | |||||
| 1000 - 1250 | 9,6 | |||||
| 16,1 | ||||||
| Итого | 25,7 | |||||
 Всего | 127,9 | |||||
Итоговая таблица аналитической группировки будет иметь следующий вид:
Таблица 2.12
Зависимость между среднесписочной численностью рабочих
и валовым выпуском продукции
| Группы предприя-тий по среднесписочной численности рабочих, чел | Число предприя- тий, ед | Среднесписочная численность рабочих, чел. | Валовой выпуск продукции, млн. грн. | ||
| всего | в среднем на одно предприятие | всего | в среднем на одно предприятие | ||
| А | 1 | 2 | 3 | 4 | 5 |
| 250 - 500 | 27,0 | 2,45 | |||
| 500 - 750 | 44,4 | 5,55 | |||
| 750 - 1000 | 30,8 | 7,70 | |||
| 1000 - 1250 | 25,7 | 12,85 | |||
| Итого | 127,9 | 5,12 |
На основании выполненной аналитической группировки можно сделать вывод: увеличение среднесписочной численности рабочих приводит к росту валового выпуска продукции в среднем на одно предприятие, т.е. между этими показателями выявлена прямая зависимость.
3. Структурная группировка предназначена для изучения состава однородной совокупности. Для её выполнения необходимо рассчитать относительные величины структуры по анализируемому показателю. Представим структурную группировку предприятий по среднесписочной численности рабочих в таблице 2.13.
Таблица 2.13
Распределение предприятий по среднесписочной численности рабочих
| Группы предприятий по среднесписочной численности рабочих, чел | Число пред-приятий, ед | Среднесписочная чис- ленность рабочих | |
| всего,чел | удельный вес,% | ||
| А | 1 | 2 | 3 |
| 250 - 500 | 27,3 | ||
| 500 - 750 | 32,2 | ||
| 750 - 1000 | 25,3 | ||
| 1000 - 1250 | 15,2 | ||
| Итого | 100,0 |
Вывод: в данной совокупности преобладают предприятия со среднесписочной численностью работающих 500 – 750 чел. (32,2%), наименьший удельный вес (15,2%), составляют предприятия с численностью 1000 – 1250 чел.
Пример 3.Имеются данные 15 фирм трех подотраслей промышленности о показателе выплаты дивидендов (%):
| Подотрасль промышленности | Показатель выплаты дивидендов, % | Тип фирмы | Количество фирм, ед |
| А | Б | В | 1 |
| 1. Производство детских игрушек | До 30 30 – 50 50 и выше | н с в | - |
| 2. Производство животного масла | До 20 20 - 40 40 и выше | н с в | - |
| 3. Производство хлопчатобумажных тканей | До 10 10 - 30 30 и выше | н с в |
Выполните типологическую группировку, выделив три группы фирм по уровню выплат дивидендов.
Решение
При выполнении типологической группировки все фирмы делят на 3 группы: с низким уровнем дивидендов (н), средним (с) и высоким (в) уровнем выплаты дивидендов. Объединим выделенные группы показателя выплаты дивидендов в три типа, независимо от подотрасли в таблице 2.14.
Таблица 2.14
Распределение фирм по уровню выплаты дивидендов
| Типы фирмы | Количество фирм | |
| единиц | удельный вес, % | |
| н | 20,0 | |
| с | 46,7 | |
| в | 33,3 | |
| Итого | 100,0 |
Как видим, наибольший удельный вес занимают фирмы со средним уровнем выплаты дивидендов. На их долю приходится 46,7 %.
Пример 4.В группе студентов второго курса обучаются 24 человека, из них 20 студентов женского пола и 4 – мужского. Постройте альтернативный ряд распределения.
Решение
Пол студента – альтернативный признак, поэтому образуем две группы и определим удельный вес каждой группы в общей численности студентов. Результаты группировки представим в таблице 2.15.
Таблица 2.15
Распределение студентов группы второго курса по полу
| Группы студентов по полу | Число студентов, чел. | Удельный вес в общей численности, % |
| Женский | 83,3 | |
| Мужской | 16,7 | |
| Итого | 100,0 |
Таким образом, на долю студентов женского пола приходится 83,3 %, а на долю мужского – 16,7 %.
Пример 5.Имеются данные о распределении филиалов банка “Маяк” по размеру прибыли:
| I регион | II регион | ||||
| Номер груп- пы | Группы филиалов банка по размеру прибыли, тыс.грн. | Удельный вес банков, в % к итогу | Номер груп- пы | Группы филиалов банка по размеру прибыли, тыс. грн. | Удельный вес банков, в % к итогу |
| I | До 100 | 4,3 | I | До 50 | 1,0 |
| II | 100-200 | 18,3 | II | 50-70 | 1,0 |
| III | 200-300 | 19,5 | III | 70-100 | 2,0 |
| IV | 300-500 | 28,2 | IV | 100-150 | 10,0 |
| V | Свыше 500 | 29,7 | V | 150-250 | 18,0 |
| VI | 250-400 | 21,0 | |||
| VII | 400-500 | 23,0 | |||
| VIII | Свыше 500 | 24,0 | |||
| Итого | 100,0 | Итого | 100,0 |
Сравните структуру филиалов банка “Маяк” по размеру прибыли, за основу приняв интервалы группировки I-го региона.
Решение
Приведенные данные не позволяют произвести сравнение распределения отделений банка “Маяк” в двух регионах по размеру прибыли, так как несопоставимы по интервалам группировки.
По второму региону произведем вторичную группировку филиалов банка путем пересчета частот, т.е. удельного веса банков. В первую вновь образованную группу филиалов второго региона с размером прибыли до 100 тыс. грн. войдут первые три группы филиалов, удельный вес которых равен 4% (гр.2 табл.2.16). Во вторую группу, т.е. в интервал от 100 до 200 тыс. грн. войдет четвертая группа филиалов, т.е. 10%, а также часть пятой группы.
Для определения удельного веса этой части рассчитываем, сколько частот приходится на единицу интервала, и умножаем на размер признака, который должен перейти в новый интервал, т.е.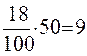 
. И тогда доля второй группы после пересчета составит 19 (10 + 9). В последнюю, пятую группу филиалов банка, с размером прибыли свыше 500 тыс. грн. войдет вся восьмая группа, на долю которой приходится 24% филиалов. Представим расчеты в таблице 2.16.
Таблица 2.16
Расчетная таблица вторичной группировки филиалов банка “Маяк”
| Номер груп-пы | I регион | II регион | ||
| Группы филиалов банка по размеру прибыли, тыс.грн | Удельный вес банков, в % к итогу | Группы филиалов банка по размеру прибыли, тыс.грн | Удельный вес банков, в % к итогу | |
| 1 | 2 | 3 | 4 | 5 |
| I | До 100 | 4,3 | До 100 | 1 + 1 +2 = 4.0 |
| II | 100 - 200 | 18,3 | 100 - 200 |  |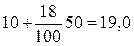
| III | 200 - 300 | 19,5 | 200 - 300 |  |
| IV | 300 - 500 | 28,2 | 300 - 500 | (21-7) + 23 =37,0 |
| V | Свыше 500 | 29,7 | Свыше 500 | |
| Итого | 100,0 | Итого | 100,0 |
В результате вторичной группировки получим следующие сопоставимые данные (табл.2.17)
Таблица 2.17
Распределение филиалов банка “Маяк” по размеру
прибыли в двух регионах
| Номер группы | Группы филиалов банка по размеру прибыли, тыс. грн | Удельный вес группы филиалов банка в % к итогу | |
| I регион | II регион | ||
| А | Б | ||
| I | До 100 | 4,3 | 4,0 |
| II | 100 - 200 | 18,3 | 19,0 |
| III | 200 - 300 | 19,5 | 16,0 |
| IV | 300 - 500 | 28,2 | 37,0 |
| V | Свыше 500 | 29,7 | 24,0 |
| Итого | 100,0 | 100,0 |
Пример 6.Имеются данные о величине доходов 10 малых предприятий.
| Номер предприятия | ||||||||||
| Размер дохода, тыс.грн |
Выполните группировку малых предприятий с прогрессивно возрастающими в арифметической прогрессии интервалами.
Решение
1. По формуле Стерджесса определим количество групп:
k = 1 + 2,233 lg n; k = 1 + 2,233 · 1,3 = 3.
Величина первого интервала будет равна:
тыс. грн.
3. Определим последующие интервалы: h2 = 2h;
h2 = 2 ·196 = 392 тыс.грн; h3 = 3h; h3 = 3 · 196 = 588 тыс.грн
4. Сформируем группы предприятий по размеру дохода, тыс. грн.: [15 - 211], [211 - 603], [603 – 1161].
5. Результаты группировки представим в таблице 2.18.
Таблица 2.18
Группировка малых предприятий по размеру дохода
| Группы предприятий по размерам доходов, тыс.грн | Кол-во предприятий, ед |
| 15-211 | |
| 211-603 | |
| 603-1191 | |
| Итого |