Обернена матриця. Приклади обчислення

Множення рядка на стовпець

Матриці однакового розміру можна віднімати і додовати

Любу матрицю можна помножити на число

Множення матриці на стовпець

Можливість множення матриці на матрицю

Матрицю A, записану зліва, можна помножити на матрицю B, записану справа, тоді і тільки тоді, коли кількість стовпців матриці А дорівнює числу рядків матриці В.

Правило множення матриці на матрицю

Кожен рядок лівої матриці множиться на стовпчик правої матриці

Обернена матриця. Приклади обчислення

Знаходження оберненої матриці є важливою складовою в розділі лінійної алгебри. З допомогою таких матриць, якщо вони існують, можна швидко знайти розв'язок системи лінійних рівнянь.

Матриця А^-1називається оберненою до матриці А, якщо виконуються наступні рівності

.АА^-1= А^-1А=Е

Якщо визначник матриці А відмінний від нуля, то матрицю називають неособливою або невиродженою.

Для того, щоб матриця мала обернену необхідно і достатньо, щоб вона була невиродженою.

АЛГОРИТМ ЗНАХОДЖЕННЯ ОБЕРНЕНОЇ МАТРИЦІ

Нехай маємо квадратну матрицю

і потрібно знайти обернену до неї. Для цього потрібно виконати наступні дії:

1. Знайти визначник матриці.|А|=∆ . Якщо він не рівний нулю то виконуємо наступні дії. В іншому випадку дана матриця вироджена і для неї не існує оберненої.

2. Знайти алгебраїчні доповнення елементів матриці А. Вони рівні мінорам, помноженим на

-1в степені суми рядка і стовпця, для якого шукаємо.

3. Скласти матрицю з алгебраїчних доповнень елементів матриці Ата протранспонувати її. Ця матриця називається приєднаною або союзною і позначається A^~.

4. Поділити приєднану матрицю на детермінант 1/∆. Отримана матриця буде оберненою та задовільнятиме властивостям, які викладені на початку статті.

5)Метод Гауса розв’язування систем лінійних рівнянь складається із двох кроків: в першому із них система шляхом виключення невідомих (першого – із другого рівняння, першого і другого – із третього зводиться до трикутникового виду). У другому кроці із третього рівняння знаходимо третє невідоме, а із другого (після підстановки в нього значення третього невідомого) знаходимо друге невідоме. І, нарешті, із першого рівняння (після підстановки в нього значень другого і третього невідомих) знаходимо значення першого невідомого.

Метод Гауса. Виключимо невідоме X₁ із другого рівняння, для чого помножимо перше рівняння на 5, а друге – на 2 і віднімемо перше одержане від другого одержаного рівняння. А далі віднімемо перше рівняння від третього. В результаті одержимо систему, яка має трикутникову форму

Виконання необхідних дій в зворотному напрямі дозволяє одержати:

6)Метод Крамера. Обчислимо визначник системи ∆, тобто визначник, укладений із коефіцієнтів при невідомих : x₁,x₂,x₃

Далі знаходимо значення допоміжних визначників ∆₁ ∆₂ ∆₃. У випадку ∆₁ стовпцем вільних членів замінений перший стовпець:

У випадку ∆₂ стовпцем вільних членів замінений другий стовпець:

У випадку ∆₃ стовпцем вільних членів замінений третій стовпець:

Тоді

7) Система лінійних рівнянь. Матричний метод

Задана система N лінійних алгебраїчних рівнянь (СЛАР) з N невідомими x₁,x₂,..,x_N коефіцієнтами при яких є елементи матриці A(a_ij), а вільними членами є числа b₁,b₂,..,b_N

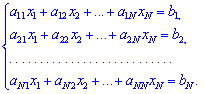
Позначимо через X– матрицю-стовпець невідомих, через B– матрицю-стовпець вільних членів. Тоді попередню систему рівнянь можна записати у вигляді матричного рівняння:

A˟X=B

Якщо квадратна матрицяA має відмінний від нуля визначник ∆, то для неї існує обернена

A^-1. Помноживши зліва в цьому рівнянні на A^-1, одержимо

Враховуючи, що A^-1 A=E і E*X=X, одержимо матричний розв'язок системи

X= A^-1 B

Знаходження матричного розв'язку називається матричним способом розв'язування системи лінійних алгебраїчних рівнянь (СЛАР).

8)Геометрич вектором – назив напрямлений відрізок.

Довжина вектора (модуль)- це відстань між почат і кінцем |a|=

Вектор в якого початок і кінець збігається- назив нульовим вектором

2 вектори назив(колінеарними)- якщо вони лежать на одній прямій або на паралельн прямих

Вектори які лежать в одній площині або в паралельн площинах – назив компланарними

Два вектори – назив рівними якщо вони колінеарні однаково напрямлені і мають рівні довжини

;

Вектор довжина якого =1 – назив одиничним.

Одиничний вектор який співпадає з напрямком осей координ площини – назив ортам.

9)Розклад вектора за ортами координ осей a=(x,y,z)

a=xi+yj+zk

a(2i3i-1)

a=2i+3j-k

A(a_xa_ya_z)

B(b_xb_yb_z)

AB=(b_x-a_x,b_y-a_y,b_z-a_z)

X= Y= Z=

Сумма двух векторов, заданных координатами

Пусть заданы a=(a_x,a_y) и b=(b_x,b_y) , тогда вектор c=a+bимеет координаты (a_x+b_x, a_y+b_y)

Довжина вектора (модуль)- це відстань між почат і кінцем |a|=

a+b=(a_x+b_x,a_y+b_y,a_z+b_z)

a-b= (a_x-b_x,a_y-b_y,a_z-b_z)