Метод Зейделя решения СЛАУ

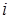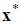Под методом Зейделя обычно понимается такое видоизменение метода простых итераций (6.3) решения СЛАУ, приведенных к виду (6.2), при котором для подсчета -й компоненты -го приближения к искомому вектору используются уже найденные на этом, т.е. -м шаге, новые значения первых 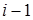компонент. Это означает, что если система (6.1) тем или иным способом сведена к системе (6.2) с матрицей коэффициентов и вектором свободных членов ,то приближения к ее решению по методу Зейделя определяются системой равенств

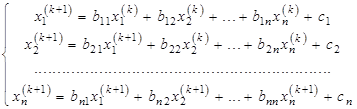(6.12)

где 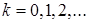, a – компоненты заданного (выбранного) начального вектора .

Остановимся подробнее на случае, когда приведение системы (6.1) к виду (6.2) основано на представлении (6.7), т. е. когда метод Зейделя есть модификация метода Якоби. Запись соответствующих расчетных формул здесь сводится к верхней индексации системы (6.10) по типу (6.12):

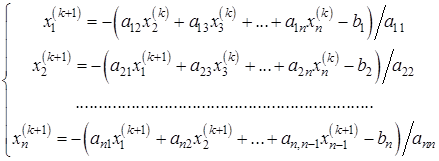(6.13)

где 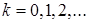; 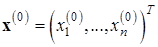задается.

Для анализа сходимости метода Зейделя (6.13) обратимся к его векторно-матричной форме. Легко видеть, что если неявный вид метода Якоби, вытекающий из представления (6.7) системы (6.1), есть

(сравните с (6.9)),

то равнозначный (6.13) неявный вид метода Зейделя в векторно-матричных обозначениях суть

.

Следовательно, тот же вектор 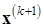,который фигурирует в левой части совокупности равенств (6.13), может быть получен по формуле

(6.14)

Последнее выражение определяет не что иное, как МПИ (6.3) для системы вида (6.2), где

,

т. е. результат применения одного шага метода Зейделя (6.13), полученного на основе – разложения матрицы ,можно расценивать, как шаг МПИ для эквивалентной (6.1) задачи о неподвижной точке

(6.15)

(разумеется, если треугольная матрица обратима). Эта связь между методом Зейделя и методом простых итераций позволяет легко переформулировать некоторые утверждения о сходимости МПИ применительно к методу Зейделя (6.13).

Теорема 6.5.Для сходимости метода Зейделя (6.13) необходимо и достаточно, чтобы все корни уравнения

(6.16)

были по модулю меньше единицы.

Прямым следствием теоремы 6.2 для метода Зейделя (6.13) является следующая теорема.

Теорема 6.6.Пусть 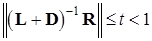. Тогда при любом начальном векторе метод Зейделя (6.13) сходится к решению 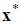системы (6.1) и справедливы оценки погрешности

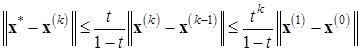(6.17)

Ясно, что для непосредственного использования оценок (6.17) нужно предварительно выполнить обращение треугольной матрицы и перемножить матрицы и 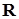. В таком случае частично теряется смысл в поэлементной реализации метода Зейделя (6.13);вместо этого можно проводить итерации по формуле (6.14) до тех пор, пока не выполнится услови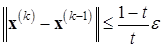е , где 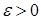– требуемая точность. В частности, такой подход может быть рекомендован при решении СЛАУ методом Зейделя на компьютерах с векторной обработкой информации.

Более подходящие для использования оценки погрешности метода Зейделя (6.13) можно получить, разлагая матрицу 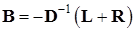(см. (6.11)) в сумму двух строго треугольных матриц, т.е. полагая

,где

, .

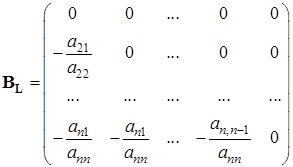С ними эквивалентное (6.1) уравнение (6.2) приобретает вид ,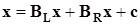

т.е. для решения 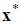будет точным равенство ,

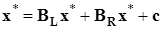а метод Зейделя (6.13) – соответственно .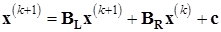

Из двух последних равенств получаем следующее:

.

Это равенство, записанное в виде (6.18)

можно расценивать как точную связь между погрешностям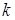и -го и 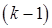-го приближений в методе Зейделя (6.13). Отсюда, переходя к нормам, легко вывести априорную оценку погрешности, что можно оформить в виде следующего утверждения.

Теорема 6.7.Пусть 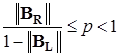. Тогда метод Зейделя (6.13) определяет сходящуюся последовательность 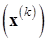при любом начальном векторе , и имеет место оценка

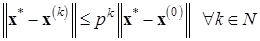
Как и у предыдущей, у этой теоремы имеются свои недостатки, затрудняющие ее применение: нужно знать меру близости начального приближения к решению 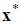. Ценность ее скорее в том, что в ней фигурирует легко вычисляемый коэффициент 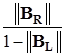связи ошибок результатов двух соседних итерационных шагов, характеризующий быстроту сходимости метода Зейделя (6.13). При организации практических вычислений по формулам (6.13) целесообразнее ориентироваться на следующий результат.

Теорема 6.8.Пусть 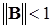, (где – матрица (6.11)). Тогда для определяемой методом Зейделя (6.13) последовательности приближений справедлива апостериорная оценка погрешности

.

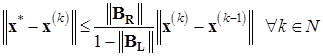Из теоремы 6.8 вытекает следующая, более удобная на практике, формулировка.

Следствие 6.1.Пусть –первое из натуральных чиселk, с которым при заданном 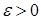для генерируемой процессом Зейделя (6.13) последовательности векторов 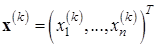некоторых согласованных нормах выполняется равенство .

Тогда за решение 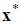системы (6.1) может быть принят вектор , и абсолютная погрешность при этом не будет превышать (в выбранной норме).

Условия сходимости методов Зейделя и простых итераций, вообще говоря, различаются. Но некоторые достаточные условия можно применять к обоим методам одновременно.