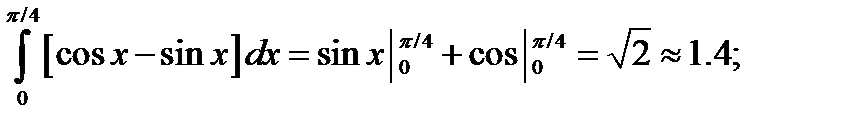Вычисление площади в полярных координатах
Тема. Вычисление площадей в декартовых и полярных координатах
Занятие 11.
Используя первообразную, можно вычислять площади плоских фигур, границы которых являются не только отрезками прямых линий.
| Y |
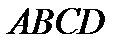 , ограниченную графиком непрерывной функции
, ограниченную графиком непрерывной функции 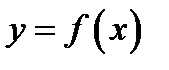 , отрезками прямых
, отрезками прямых 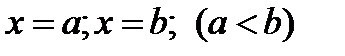 и отрезком оси
и отрезком оси 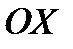 .
.
| F |
| A |
| B |
| E |
| X |
| O |
| a |
| b |
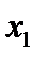
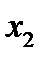
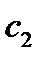
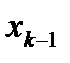 ®
® 


Разобьём отрезок 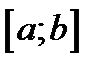 на
на  ячеек
ячеек 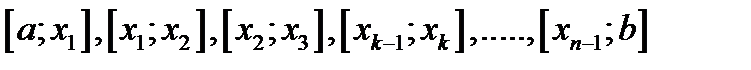 . В каждой
. В каждой
ячейке выбираем число  и составляем интегральную сумму
и составляем интегральную сумму  . Эта интегральная сумма даёт нам сумму площадей прямоугольников. Отсюда
. Эта интегральная сумма даёт нам сумму площадей прямоугольников. Отсюда  площадь трапеции
площадь трапеции  . Переходя к
. Переходя к
пределу получаем точный результат

Мы получили замечательный результат. Площадь криволинейной трапеции, ограниченной
графиком непрерывной функции 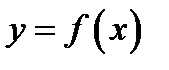 , отрезками прямых
, отрезками прямых 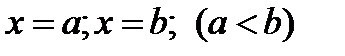 и отрезком оси
и отрезком оси 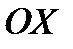 , равна определённому интегралу
, равна определённому интегралу  .
.
| B |
| A |
| Y |
Y=f(x)
| X |
| O |
| a |
| b |
рис.1
Определение 13.1.Криволинейной трапецией 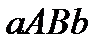 назовём область на координатной плоскости
назовём область на координатной плоскости 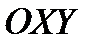 , ограниченную линиями
, ограниченную линиями 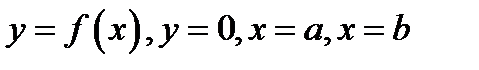 , рис.1
, рис.1
В примере 1 мы доказали, что если функция 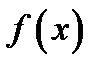 непрерывная, то площадь
непрерывная, то площадь
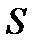 криволинейной трапеции
криволинейной трапеции 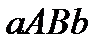 вычисляется по формуле
вычисляется по формуле
 (13.1)
(13.1)
Замечание.Если график функциилежит ниже оси  рис.2, то очевидно
рис.2, то очевидно
Рис.2
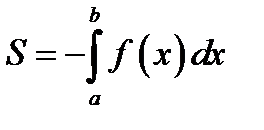 (13.2)
(13.2)
Можно получать аналогичные формулы, используя понятие дифференциала функции.
Рассмотрим опять трапецию и на отрезке 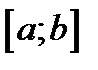 возьмём произвольно точку
возьмём произвольно точку  и проведём через
и проведём через
неё перпендикулярный отрезок , длиной  . Если теперь в каждой точке проделать эту операцию то вся площадь будет покрыта этими отрезками. Этот отрезок можно теоретически считать бесконечно тонким прямоугольником (неделимым далее ) с основанием
. Если теперь в каждой точке проделать эту операцию то вся площадь будет покрыта этими отрезками. Этот отрезок можно теоретически считать бесконечно тонким прямоугольником (неделимым далее ) с основанием  и высотой
и высотой  . Площадь такого прямоугольника можно назвать дифференциальным элементом искомой площади
. Площадь такого прямоугольника можно назвать дифференциальным элементом искомой площади 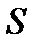 . Его площадь будет равна
. Его площадь будет равна 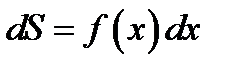 . Полная площадь формально получается сложением всех площадей этих неделимых прямоугольников. А поскольку основания прямоугольников сплошь заполняют отрезок
. Полная площадь формально получается сложением всех площадей этих неделимых прямоугольников. А поскольку основания прямоугольников сплошь заполняют отрезок 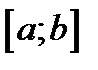 , то вместо операции суммирования применяется операция интегрирования
, то вместо операции суммирования применяется операция интегрирования
 (13.3)
(13.3)
Как вычислить площадь, лежащую между двумя графиками при 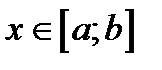 (рис.3)
(рис.3)
| С |
| В |
| а |
| в |
| D |
| А |
Рис.3
Искомая площадь  равна площади аВСв + площадь Аав
равна площади аВСв + площадь Аав 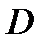 . Следовательно, из
. Следовательно, из
свойства III (формула (11.8)) и формул (13.1),(13.2). следует формула вычисления площади,
лежащей между графиками функций
 (13.4)
(13.4)
Вычисление площади в полярных координатах.
Из школы хорошо известно, что площадь кругового сектора (рис.4)вычисляется по формуле
| O |
| φ |
| R |
рис.4
 (13.5)
(13.5)
Пусть ищется площадь 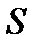 , ограниченная кривой
, ограниченная кривой 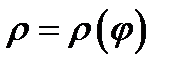 и радиусами векторами с углами
и радиусами векторами с углами  рис. 5.
рис. 5.
рис.5
1шаг. Данная площадь разбивается на сумму круговых секторов.
Пронумеруем :
1)центральные углы каждого кругового сектора так : 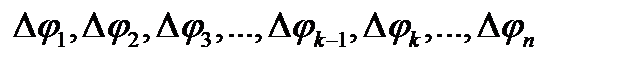 ;
;
2) радиусы круговых секторов обозначим так:  ;
;
2шаг. Сумма площадей круговых секторов равна
 (13.6)
(13.6)
3шаг.
Так как функция 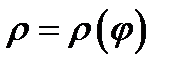 непрерывна, то на основании теоремы 11.1 определённый интеграл от неё существует. Следовательно, переходя к пределу при
непрерывна, то на основании теоремы 11.1 определённый интеграл от неё существует. Следовательно, переходя к пределу при 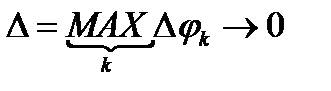 получаем
получаем 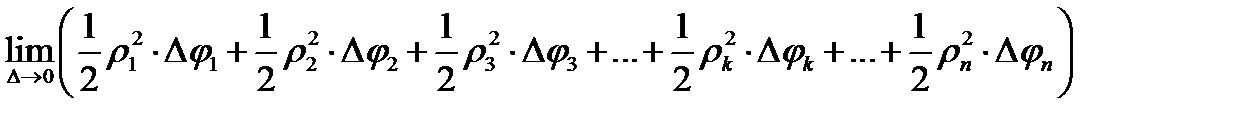 =
= 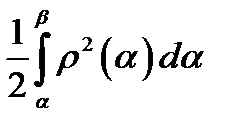
По определению если существует предельное значение суммы круговых секторов (13.6), то
Это предельное значение равно площади криволинейного сектора. Отсюда
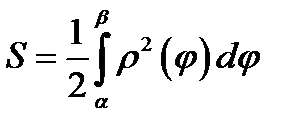 (13.7)
(13.7)
По аналогии с формулой (13.4) площадь усеченного криволинейного сектора даётся формулой
рис.6
 (13.8)
(13.8)

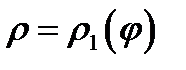
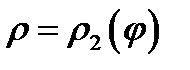
рис.5
Рассмотрим соответствующие примеры.
Пример 1. Вычислить площадь области , ограниченной линиями  .
.
Решение. Границы заданы в декартовых координатах. Основной фигурой при вычислении площадей здесь является трапеция. Вычисление площади производим по формуле (13.4)
 =
= 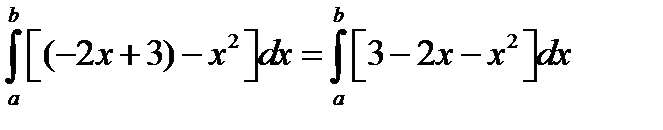
Сделаем эскиз графика см.рис.6. Границы
 являются абсциссами точек пересечения
являются абсциссами точек пересечения
графиков. Мы находим их, решая систему уравнений

Отсюда  . Подставляя данные в формулу площади, получаем
. Подставляя данные в формулу площади, получаем
рис.6

Пример 2. Вычислить площадь области , ограниченной линиями 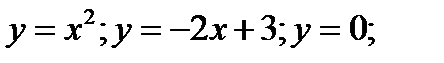
Решение. Границы заданы в декартовых координатах. Основной фигурой при вычислении площадей здесь является трапеция. Вычисление площади производим по формуле (13.1)

В данном случае
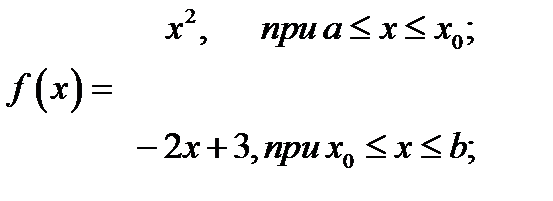
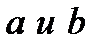 находим , решая системы (почему?)
находим , решая системы (почему?)

рис.7.
Откуда 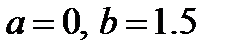 ; Абсциссу
; Абсциссу 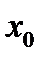 находим из условия пересечения линий
находим из условия пересечения линий 

 .
.
Подставляя данные в формулу (11.1), находим площадь
 =
=
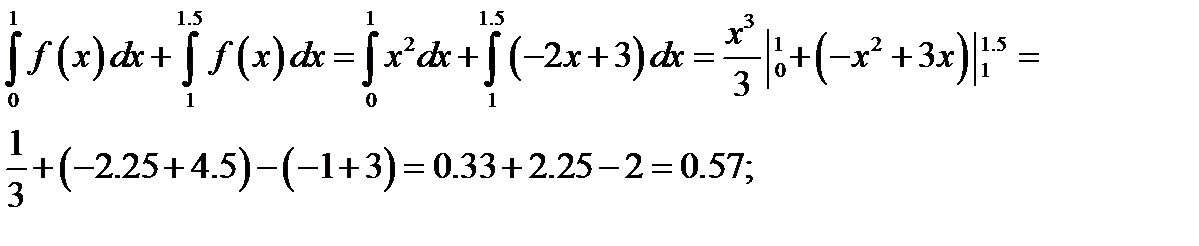
Пример 3. Вычислить площадь области , ограниченной линиями 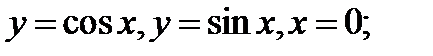
Решение. Границы заданы в декартовых координатах. Основной фигурой при вычислении площадей здесь является трапеция. Вычисление площади производим по формуле (13.4)


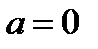
Очевидно, что 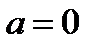 . Абсциссу
. Абсциссу 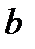
находим из условия пересечения линий 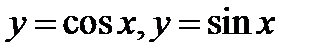 , решая систему
, решая систему

Откуда  ;
;
рис.8
 =
=