Модель Энгсета

Модель Энгсета (рисунок 3.12) применяется, как правило, для расчета вероятности потерь при малом количестве источников вызовов и справедлива при таких предположениях:

- вызовы, поступающие на вход системы, образуют примитивный поток, поэтому параметр потока вызовов в момент занятости х каналов системы пропорционален числу свободных источников вызовов, т.е.

, ,

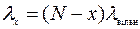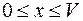где 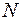- общее число источников вызовов;

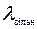- интенсивность поступления вызовов от свободного источника;

- длительность занятия подчиняется экспоненциальному распределению с параметром 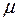, параметр потока освобождений ;

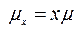- вызов, не принятый к обслуживанию в момент поступления, теряется, не влияя на моменты поступления последующих вызовов;

- любой из V выходов пучка доступен, когда он свободен, для любого поступающего вызова.

- исходной для расчета является поступающая нагрузка;

- система находится в стационарном режиме.

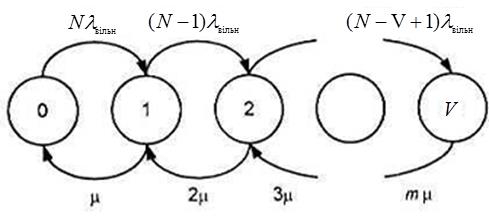
Рисунок 3.12 – Диаграмма переходов, соответствующая модели Энгсета

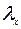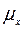Подставляя значения параметров и , в выражение (3.6), получим

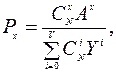
где 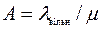- максимальное значение поступающей интенсивности нагрузки;

.

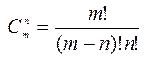Вероятность занятия всех линий пучка

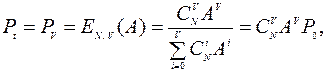(3.7)

где .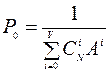

Выражение (3.7) определяет вероятность потерь по времени и носит название формулы Энгсета. Полученный результат позволяет рассчитать вероятность, того, что будут заняты всеканалы, т.е. система окажется заблокированной.

Параметр потерянного потока вызовов:

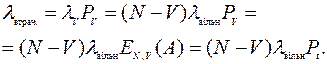
Вероятность потерь по вызовам определяется как отношение параметра потерянного потока вызовов к среднему значению параметра поступающего потока вызовов

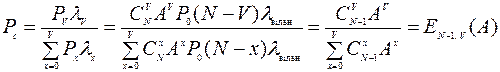. (3.8)

Вероятность потерь по нагрузке определяется выражением

.

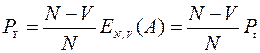Таким образом, в пучке емкостью 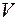каналов, на который поступает примитивный поток вызовов, потери по вызовам при наличии 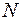источников равны потерям по времени при наличии 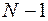источников, т.е.

.

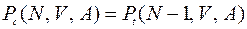З наведених виражень видно, що для ймовірностей втрат справедлива нерівність

.

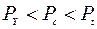Прямой расчет формулы Энгсета во многих практических случаях может быть затруднен. Поэтому для расчета пользуются рекурентным соотношением

,

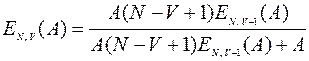последовательно вычисляя 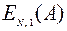, , 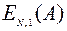…, 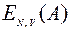при начальном значении .

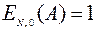Выражение (3.8), определяющее вероятность потерь по вызовам 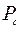, табулировано для широкого диапазона значений 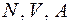. По этим же таблицам определяют вероятность потерь по времени, исходя из равенства .

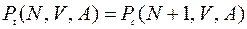Соотношение между параметром потока и нагрузкой, поступающей от одного источника 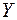.Рассмотрим систему без потерь, т.е. систему, в которой число каналов равно числу источников вызовов ( 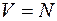).В такой системе каждый источник вызовов может обслуживаться независимо от состояния других источников. Поэтому достаточно рассмотреть случай 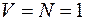. При этом можно получить, что

, .

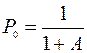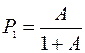Вероятность 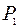в рассматриваемом случае есть доля времени, в течение которого источник в системе без потерь занят, что численно соответствует интенсивности нагрузки 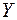, поступающей от одного источника

,

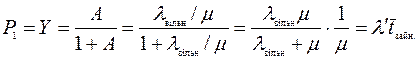где 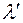- реальный параметр потока вызовов, поступающего от источника вызовов при отсутствии потерь; 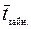- среднее время занятия.

Учитывая, что 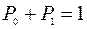, можно записать

,

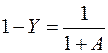откуда

.

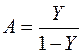Поэтому при численных расчетах осуществляют замену вида .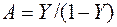

Общая поступающая нагрузка при этом будет равна

.

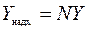Среднее число занятых каналов (обслуженная нагрузка):

.

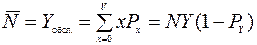И в заключение, рассмотрим графики для вероятностей потерь по вызовам для моделей Энгсета и Эрланга, приведенные на рисунке 3.13 (для модели Эрланга потери по времени, вызовам и нагрузке совпадают),

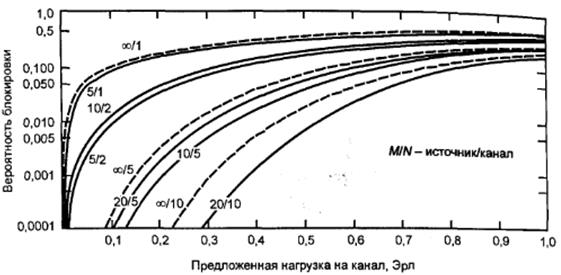
Рисунок 3.13 – Вероятности потерь по вызовам

для моделей Эрланга и Энгсета

Из рисунка 3.13 следует, что вероятность потерь по вызовам, полученная при помощи формулы Энгсета несколько меньше, чем вероятность потерь по вызовам полученная в соответствии с формулой Эрланга.

Таким образом, модель Энгсета часто применяется для расчета вероятности потерь при небольшом числе источников вызовов. В этих случаях уменьшение интенсивности входного потока за счет исключения источника, который получил обслуживание, оказывается существенным. При большом количестве источников доля интенсивности входного потока от каждого из них по сравнению с обшей интенсивностью оказывается незначительной. В этих случаях результаты расчета по формулам Эрланга и Энгсета будут весьма близкими. В пределе, при 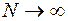, а 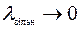формула Энгсета непосредственно переходит в формулу Эрланга.