Внутренне- и внешне устойчивые множества вершин
Дадим определения сразу для неориентированного и ориентированного случаев, учиты-вая, что эти определения очень похожи (отличия будем указывать в скобках). Две различные вершины, которые соединены ребром (дугой), т.е. являющиеся концами одного и того же ребра (дуги), называются смежными. В противном случае две вершины не смежны. Множество X вершин графа G, любые две из которых не смежны, называется внутренне устойчивым, а мак- симально возможное число элементов внутренне устойчивого множества − числом внутренней устойчивости графа G (обозначается α(G)).
Сразу поясним это не очень простое понятие. Прежде всего, любое множество вершин, со-стоящее из одной вершины, является по определению внутренне устойчивым как в неориенти-рованном, так и в ориентированном случае. Действительно, определение внутренней устойчи-вости множества вершин X, как и почти все математические определения, является импликаци-ей. Его можно переформулировать так: «Если любые две разные вершины множества X не смежны, то множество X называется внутренне устойчивым» или, пользуясь определёнными в главе 1-4 кванторами, короче
( 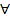 aÎX)(
aÎX)( 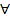 bÎX)[(a ≠b)→(a не смежна с b)]. (3)
bÎX)[(a ≠b)→(a не смежна с b)]. (3)
Но если множество X состоит из одной вершины, то посылка a ≠b импликации (3) всегда ложна, поскольку a и b – две разные вершины из множества X. Напомним, что по определению импли-кации (см. раздел 1-2.1.4), импликация с ложной посылкой всегда истинна «в силу ложности посылки». Но это и означает истиннось импликации (3), что и означает внутреннюю устойчи-вость любого одноэлемнтного множества.
Утверждение 1. Любое подмножество внутренне устойчивого множества внутренне ус-тойчиво
Действительно, по определению, во внутренне устойчивом множестве никакие две верши-ны не соединены ребром. Значит, этим же свойством обладает и любое его подмножество ■
Внутренне устойчивое множество вершин называется максимальным по включению, ес-ли оно не содержится ни в каком другом внутренне устойчивом множестве. Утверждение 1 позволяет при поиске всех внутренне устойчивых множеств ограничиться поиском только максимальных по включению внутренне устойчивых множеств. Действительно, всякое внут-ренне устойчивое множество либо само является максимальным по включению, либо содержит-ся в некотором максимальном по включению внутренне устойчивом множестве. (Заметим, что таких множеств может быть несколько). Поэтому семейство всех максимальных по включению внутренне устойчивых множеств определяет все внутренне устойчивые множества: множество является внутренне устойчивым, если оно содержится хотя бы в одном максимальном по вклю-чению внутренне устойчивом множестве.
Пример 7.Проиллюстрируем понятия внутренней устойчивости множества вершин в не-ориентированном графе. Для этого рассмотрим граф, показанный на рис.5а. На рис.5б – 5е по-казаны все максимальные по включению внутренне устойчивые множества в данном графе. На каждом из этих рисунков видно, что все выделенные большими кружками вершины не соедине-ны непосредственно друг с другом рёбрами. Ясно также, что при добавлении любой вершины все эти множества перестают быть внутренне устойчивыми – появляются рёбра. Обратим вни-мание на то, что максимальные по включению внутренне устойчивые множества могут содер-жать различное число вершин – три на рис.5б – 5г и два на рис.5д и 5е.
Множество, показанное на рис.5ж, является внутренне устойчивым, но не максимальным по включению. Оно содержится в множестве, показанном на рис.5б. Наконец, множество, пока-занное на рис.5з, не является внутренне устойчивым. Входящие в него вершины 5 и 6 соедине-ны ребром.
Поскольку максимальное число вершин во внутренне устойчивом множестве равно 3, то число внутренней устойчивости α(G) = 3.
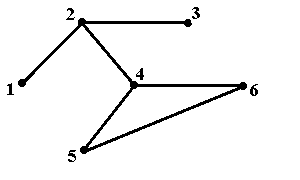 Рис.5а. Исходный граф Рис.5а. Исходный граф | 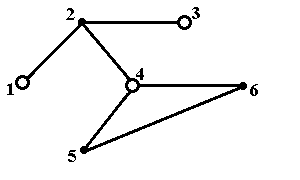 Рис.5б. Максимальное по включению внутренне устойчивое множество {1,3,4} Рис.5б. Максимальное по включению внутренне устойчивое множество {1,3,4} |
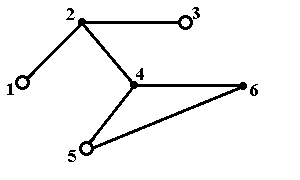 Рис.5в. Максимальное по включению внутренне устойчивое множество {1,3,5} Рис.5в. Максимальное по включению внутренне устойчивое множество {1,3,5} | 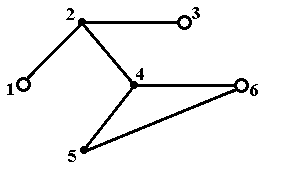 Рис.5г. Максимальное по включению внутренне устойчивое множество {1,3,6} Рис.5г. Максимальное по включению внутренне устойчивое множество {1,3,6} |
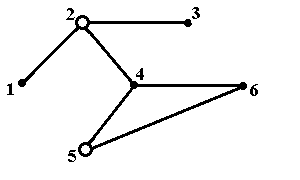 Рис.5д. Максимальное по включению внутренне устойчивое множество {2,5} Рис.5д. Максимальное по включению внутренне устойчивое множество {2,5} | 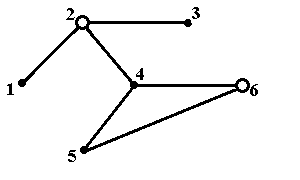 Рис.5е. Максимальное по включению внутренне устойчивое множество {2,6} Рис.5е. Максимальное по включению внутренне устойчивое множество {2,6} |
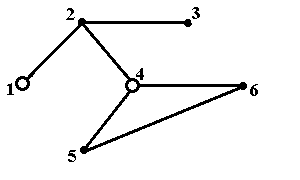 Рис.5ж. Внутренне устойчивое множество {1,4}, не максимальное по включению Рис.5ж. Внутренне устойчивое множество {1,4}, не максимальное по включению | 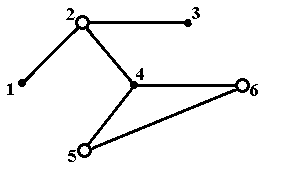 Рис.5з. Множество вершин {2,5,6}, не являющееся внутренне устойчивым Рис.5з. Множество вершин {2,5,6}, не являющееся внутренне устойчивым |
Можно проверить, что любое множество, содержащее 4 вершины, не будет внутренне ус-тойчивым. Действительно, любое внутренне устойчивое множество не может содержать ника-ких двух вершин из подмножества {4,5,6}, так как они все попарно смежны (соединены рёбра-ми). Значит, в него может входить не более одной вершины из множества {4,5,6}. Но так как в нём должно быть 4 вершины, а всего есть 6 вершин, то в него должны входить все вершины из множества {1,2,3}. А так как вершины 1 и 2 смежны, то такое множество не может быть внут-ренне устойчивым. В силу того же утверждения 1 бóльшие множества вершин также не могут быть внутренне устойчивыми ■
В произвольном графе с небольшим числом вершин максимальные по включению внут-ренне устойчивые множества могут быть найдены простым перебором всех различных подмно-жеств, начиная с множества всех вершин. Однако самый простой и эффективный подход – вни-мательно посмотреть на граф собственными глазами (и подумать собственной головой). Конеч-но, в графах, содержащих порядка 15 и более вершин, такой просмотр практически нереален. Формальные алгоритмы решения данной задачи в силу своей сложности здесь не рассматрива-ются.
Введём дальнейшие понятия. Множество X вершин графа G называется внешне устойчи-вым, если любая вершина из V  X, т.е. вершина, не принадлежащая X, смежна хотя бы с одной вершиной из X (является концом некоторой дуги, начало которой принадлежит множеству вер-шин X, в ориентированном случае). Минимально возможное число элементов внешне устойчи-вого множества называется числом внешней устойчивости графа G (обозначается β(G)). Об-ратим внимание на то, что связность вершин внутри множества X не оказывает никакого влия-ния на данное свойство. Это значит, что добавление или удаление любого ребра (дуги) между вершинами из X не повлияет ни на наличие свойства внешней устойчивости у множества X, ни на его отсутствие. Обратим внимание, что в определении не требуется, чтобы какая-нибудь вер-шина из X была бы смежной со всеми вершинами из V
X, т.е. вершина, не принадлежащая X, смежна хотя бы с одной вершиной из X (является концом некоторой дуги, начало которой принадлежит множеству вер-шин X, в ориентированном случае). Минимально возможное число элементов внешне устойчи-вого множества называется числом внешней устойчивости графа G (обозначается β(G)). Об-ратим внимание на то, что связность вершин внутри множества X не оказывает никакого влия-ния на данное свойство. Это значит, что добавление или удаление любого ребра (дуги) между вершинами из X не повлияет ни на наличие свойства внешней устойчивости у множества X, ни на его отсутствие. Обратим внимание, что в определении не требуется, чтобы какая-нибудь вер-шина из X была бы смежной со всеми вершинами из V  X. Достаточно, если любая вершина из V
X. Достаточно, если любая вершина из V  X смежна хотя бы с какой-нибудь вершиной из X. Для разных «внешних» вершин (т.е. из V
X смежна хотя бы с какой-нибудь вершиной из X. Для разных «внешних» вершин (т.е. из V  X) смежные с ними «внутренние» вершины (т.е. из X) могут (но не обязаны!) быть различны-ми.
X) смежные с ними «внутренние» вершины (т.е. из X) могут (но не обязаны!) быть различны-ми.
Заметим, что само множество всех вершин V является внешне устойчивым в силу ложнос-ти посылки. Действительно, при X = V имеем V  X = Æ, т.е. вершин, не принадлежащих X, прос-то не существует. Как и определение внутренне устойчивого множества, определение внешне устойчивого множества является импликацией:
X = Æ, т.е. вершин, не принадлежащих X, прос-то не существует. Как и определение внутренне устойчивого множества, определение внешне устойчивого множества является импликацией:
( 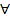 aÎV
aÎV  X)→(
X)→( 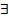 bÎX)(a смежна с b), (4)
bÎX)(a смежна с b), (4)
которая всегда верна при ложной посылке ( 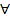 aÎV
aÎV  X).
X).
Имеет место простое
Утверждение 2. Любое множество, содержащее внешне устойчивое множества вершин, также внешне устойчиво.
Действительно, пусть внешне устойчивое множество XÍY. Для всякой вершины zÎV  Y верно zÎV
Y верно zÎV  X. Так как X – внешне устойчивое множество, то, по определению, z смежна с неко-торой вершиной wÎX (является концом дуги с началом w). А в силу включения XÍY имеем wÎY. Таким образом, начав с произвольной вершины zÎV
X. Так как X – внешне устойчивое множество, то, по определению, z смежна с неко-торой вершиной wÎX (является концом дуги с началом w). А в силу включения XÍY имеем wÎY. Таким образом, начав с произвольной вершины zÎV  Y, установили, что она смежна с некоторой вершиной wÎY (является концом дуги с началом w), что, по определению, означает внешнюю устойчивость Y ■
Y, установили, что она смежна с некоторой вершиной wÎY (является концом дуги с началом w), что, по определению, означает внешнюю устойчивость Y ■
Внешне устойчивое множество называется минимальным по включению, если оно не содержит ни одного другого внешне устойчивого множества. В силу утверждения 2, для нахож-дения всех внешне устойчивых множеств достаточно найти только минимальные внешне ус-тойчивые множества. Все остальные являются произвольными множествами, содержащими хо-тя бы одно минимальное по включению внешне устойчивое множество.
Проиллюстрируем теперь это понятие на том же графе рис.5а.
Пример 8. На рис.6а – 6е показаны все минимальные по включению внешне устойчивые множества в данном графе. На каждом из этих рисунков видно, что любая вершина, показанная чёрным кружком (как в исходном графе) соединена хотя бы с одной вершиной из внешне ус-тойчивого множества, выделенных квадратами. Ясно также, что при удалении любой вершины из внешне устойчивого множества все эти множества перестают быть внешне устойчивыми – появляются вершины, не соединённые ни с одной из оставшихся вершин. Обратим внимание на то, что минимальные по включению внешне устойчивые множества могут содержать различное число вершин – две на рис.6а – 6в и три на рис.6г – 6е.
Множество, показанное на рис.6ж, является внешне устойчивым, но не минимальным по включению. Оно содержит множества, показанные на рис.6б и 6в. Наконец, множество, пока-занное на рис.6з, не является внешне устойчивым. Вершина 3 не соединена ребром ни с верши-ной 1, ни с вершиной 4, что противоречит определению внешне устойчивого множества.
Поскольку минимальное число вершин во внешне устойчивом множестве равно 2, то чис-ло внешней устойчивости β(G) = 2.
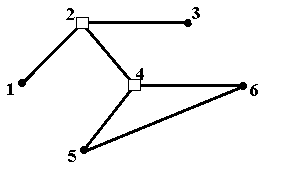 Рис.6а. Минимальное по включению внутренне устойчивое множество {2,4} Рис.6а. Минимальное по включению внутренне устойчивое множество {2,4} | 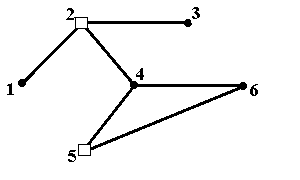 Рис.6б. Минимальное по включению внутренне устойчивое множество {2,5} Рис.6б. Минимальное по включению внутренне устойчивое множество {2,5} |
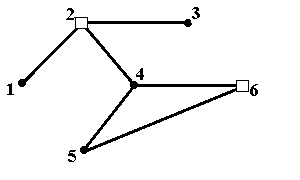 Рис.6в. Минимальное по включению внутренне устойчивое множество {2,6} Рис.6в. Минимальное по включению внутренне устойчивое множество {2,6} | 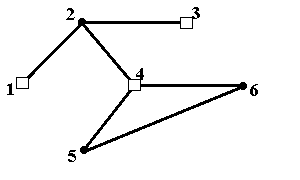 Рис.6г. Минимальное по включению внутренне устойчивое множество {1,3,4} Рис.6г. Минимальное по включению внутренне устойчивое множество {1,3,4} |
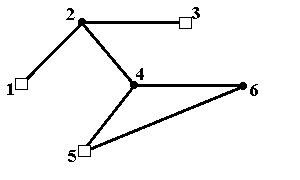 Рис.6д. Минимальное по включению внутренне устойчивое множество {1,3,5} Рис.6д. Минимальное по включению внутренне устойчивое множество {1,3,5} | 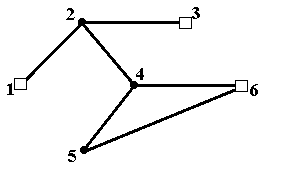 Рис.6е. Минимальное по включению внутренне устойчивое множество {1,3,6} Рис.6е. Минимальное по включению внутренне устойчивое множество {1,3,6} |
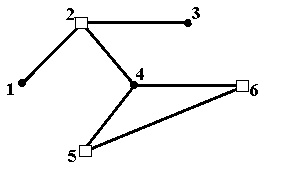 Рис.6ж. Внешне устойчивое множество {2,5,6}, не минимальное по включению Рис.6ж. Внешне устойчивое множество {2,5,6}, не минимальное по включению | 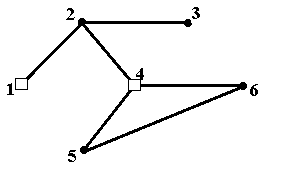 Рис.6з. Множество вершин {1,4}, не являющееся внешне устойчивым Рис.6з. Множество вершин {1,4}, не являющееся внешне устойчивым |
Видно непосредственно на рисунке, что любое множество, содержащее одну вершину, не будет внешне устойчивым – просто потому, что в исходном графе нет ни одной вершины, со-единённой со всеми остальными ■
Как и для внутренне устойчивых множеств, формальные алгоритмы решения данной зада-чи в силу своей сложности здесь не рассматриваются.
Множество X вершин графа G, одновременно внутренне и внешне устойчивое, называет-ся ядром графа G.
Напомним, что определения внутренне устойчивого множества вершин в неориентрован-ном и ориентированном случаях совпадают. Совпадают и определения ядра. Отличаются толь-ко определения внешне устойчивого множества: в ориентированном случае требуется, чтобы дуга, соединяющая множества X и V  X, имела направление от X к V
X, имела направление от X к V  X.
X.
Из определений внутренней и внешней устойчивости непосредственно следует, что:
- любая изолированная вершина графа может быть добавлена к любому не содержащему её внутренне устойчивому множеству и это расширенное множество также будет внутренне устойчивым;
- любое внешне устойчивое множество обязано содержать любую изолированную верши-ну.
Из утверждений 1 и 2 непосредственно следует
Утверждение 3.Множество вершин Z является ядром графа G тогда и только тогда, когда существуют минимальное по включению внешне устойчивое множество X и максимальное по включению внутренне устойчивое множество Y, такие, что
X 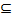 Z
Z 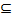 Y. (5)■
Y. (5)■
Если уже известны все минимальные по включению внешне устойчивые множества X1, …, Xs и все максимальные по включению внутренне устойчивые множества Y1, …, Yt, то утвер-ждение 3 позволяет предложить следующий
Алгоритм нахождения всех ядер графа.
1. Находим все такие пары индексов i, j, такие, что Xi 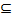 Yj.
Yj.
2. Для каждой такой пары индексов находим все множества Z, удовлетворяющие двойно-му включению
Xi 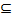 Z
Z 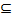 Yj. (6)
Yj. (6)
3. Из всех множеств Z, найденных на шагах 1 и 2, выделяем все различные множества. Они и являются всеми ядрами графа ■
Алгоритм применим как в неориентрованном, так и в ориентированном случаях. Если включение Xi 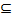 Yj ни при каких i, j не выпоняется, то это означает, что в данном графе или орграфе ядер не существуют. Заметим также, что сами списки X1, …, Xs и Y1, …, Yt никогда не являются пустыми, поскольку в любом графе и орграфе любое одноэлементное множество яв-ляется внутренне устойчивым, а множество всех вершин – внешне устойчивым, в силу ложнос-ти посылки.
Yj ни при каких i, j не выпоняется, то это означает, что в данном графе или орграфе ядер не существуют. Заметим также, что сами списки X1, …, Xs и Y1, …, Yt никогда не являются пустыми, поскольку в любом графе и орграфе любое одноэлементное множество яв-ляется внутренне устойчивым, а множество всех вершин – внешне устойчивым, в силу ложнос-ти посылки.
ккогда не выпоняется (например, если
Среди внешне усточЗаметим, что утверждения 1 – 4 верны как в неориентированном, так и в ориентированном случаях. Однако следующее утверждение верно только для неориентированных графов.
Утверждение 5. Любое максимальное по включению (т.е. не содержащееся ни в каком другом) внутренне устойчивое множество является и внешне устойчивым, т.е. является ядром ■
Поскольку в любом неориентированном (как и в любом ориентированном) графе множес-тво, состоящее из одной вершины, является внутренне устойчивым, то существует и макси-мальное по включению внутренне устойчивое множество. А оно, в силу утверждения 5, являет-ся ядром.
Утверждение 5 даёт гарантию существования ядра для неориентированных графов. А простой пример отсутствия ядра в орграфе даётся ниже, в прмере 10.
Пример 9. Рассмотрим снова граф на рис.5а. Максимальными по включению внутренне устойчивыми множествами являются множества {1,3,4}, {1,3,5}, {1,3,6}, {2,5}, {2,6} (см. рис. 5). Минмальными по включению внешне устойчивыми множествами являются множества {2, 4}, {2,5}, {2,6}, {1,3,4}, {1,3,5}, {1,3,6} (см. рис.6). В силу утверждения 4 любое ядро содержит-ся в некотором множестве из 1-го списка и содержит некоторое множестве из 2-го списка. В данном случае имеется пять таких множеств, причём во всех 5-и случаях оба включения (5) вы-полняются как равества:
{2,5} 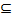 Z
Z 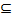 {2,5}, {2,6}
{2,5}, {2,6} 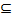 Z
Z 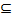 {2,6}, {1,3,4}
{2,6}, {1,3,4} 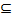 Z
Z 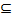 {1,3,4}, {1,3,5}
{1,3,4}, {1,3,5} 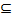 Z
Z 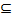 {1,3,4},{1,3,4}
{1,3,4},{1,3,4} 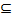 Z
Z 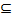 {1,3,4}.
{1,3,4}.
Поэтому множества вершин {2,5}, {2,6},{1,3,4}, {1,3,5}, {1,3,6} представляют собой все ядра в данном графе ■
Пример 10. На рис.7 показан орграф из примера 6 (сеть питания) с пронумерованными вершинами 1 – 5. В этом орграфе внутренне устойчивыми множествами являются все 1-элемен-тные множества {1}, {2}, {3}, {4}, {5} и 2-элементные множества {1,3}, {1,4}, {2,4}, {4,5}. Других внутренне устойчивых множеств в данном орграфе нет. Максимальными по включению являются только эти множества.
Одноэлементных внешне устойчивых множеств в данном случае нет (так как нет ни одной вершины, откуда дуги ведут во все остальные). Единственным двухэлементным внешне устой-чивым множеством является {1, 4} (так как дуги á1, 5ñ, á1, 2ñ и á4, 3ñ ведут из {1, 4} в 5, 2 и 3, т.е. во все остальные вершины, в соответствии с определением). В силу включений (5) единственным ядром является множество {1,4}, так как только оно удовлетворяет этим включениям ■
Само существование ядра для орграфов, в отличие от неориентированных графов, как ука-зывалось выше, не гарантировано, что демонстрирует следующий
Пример 11.Рассмотрим простой орграф без петель, показанный на рис.8. Проверим, что у
него нет ядра. Предположим, что ядро состоит из одной вершины 1. Но тогда нет дуги, ведущей из 1 в 3, т.е. оно не является внешне устойчивым. Аналогично, ядро не может состоять из вер-шины 2 или вершины 3. Предположим, что ядро состоит из двух вершин, скажем, вершин 1 и 2. Тогда есть дуга из 2 в 3, т.е. оно является внешне устойчивым. Но оно не является внутренне устойчивым, так как в него входят вершины 1 и 2, соединённые дугой. Аналогично для мно-жеств {1, 3} и {2, 3}. Наконец, множество всех вершин {1, 2, 3} является внешне устойчивым, но не является внутренне устойчивым. Таким образом, в данном орграфе ядер нет ■
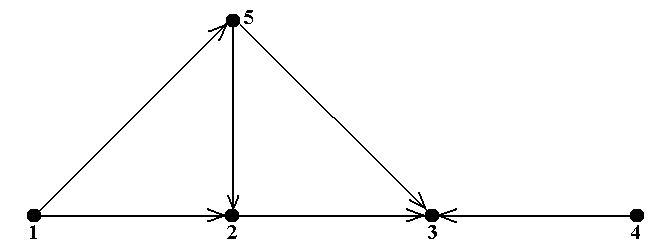 Рис.7 Рис.7 | 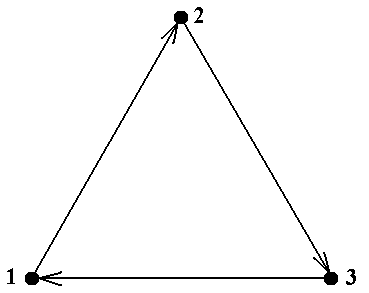 Рис.8 Рис.8 |
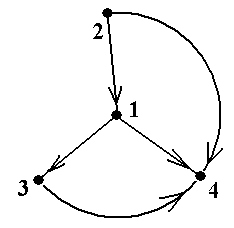
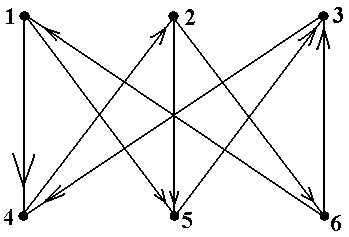
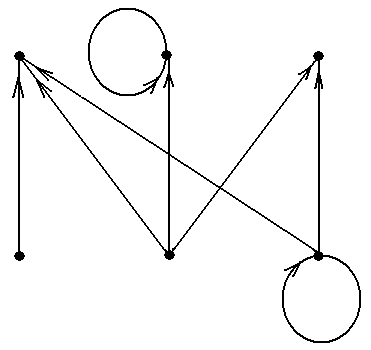
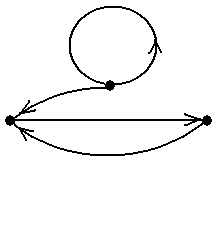
Задание 3.Ворграфах, показанных на рис.10, найти
1) одно максимальное и одно минимальное по числу вершин ядро;
2) если все ядра содержат одно и то же число вершин, найти два разных ядра;
3) если имеется всего одно ядро, найти его;
4) если ядер не существует, объяснить этот факт ■
Пути в графах
Как и в разделе 2, будем давать определения сразу для неориентированного и ориентиро-ванного случая, указывая отличия в скобках. Наиболее общим понятием является понятие пути (орпути). Путём (орпутём) в графе (орграфе) называется чередующаяся последовательность μ вершин и рёбер (дуг), начинающаяся и кончающаяся в вершинах:
μ = áv0, b1, v1, b2, ..., vk-1, bk,vkñ, (4)
такая, что вершины vi и vi+1 соединены ребром (дугой) bk.
Вершина v0 называется началом пути (орпути) μ, вершина vk – концом пути (орпути) μ, а число k, равное числу рёбер (дуг), входящих в путь (орпуть) – его длиной. Говорят также, что путь μсоединяет вершины v0 и vk (орпуть μ ведёт изv0 в vk). Обратным путём для пути μ на- зывается путь μ-1 = ávk, bk, vk-1, bk-1, ..., v1, b1,v0ñ. Другими словами, путь μ-1состоит из тех же самых вершин и рёбер, но проходимых в обратном порядке. Обратим внимание, что обратный путь определён только в неориентированном случае.
Цепью (орцепью) называется путь (орпуть), в котором все рёбра (дуги) различны. Прос-
Рис.7
 Рис.8 Рис.8 |  Рис.9 Рис.9 | ||
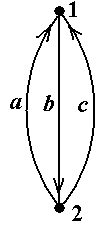 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
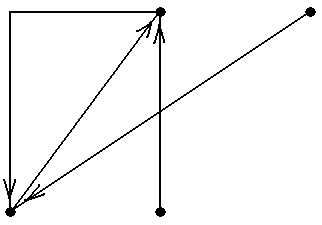 | 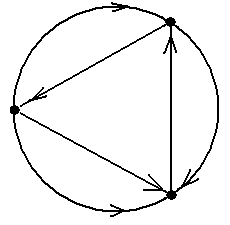 | 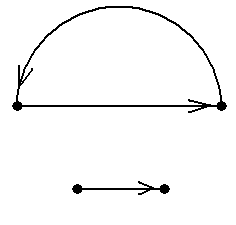 | |
Рис. 10
той цепью (орцепью) называется цепь (орцепь), в которой все вершины различны. Путь (ор-путь), в котором начало и конец совпадают, называется циклическим путём (орпутём). Цик-лический путь, являющийся цепью (орцепью), называется циклом (орциклом). Цикл (орцикл), в котором все вершины, кроме начала и конца, различны и не совпадают с началом, называется простым циклом (орциклом).
Говорят, что не циклический путь νсодержится в не циклическом пути μ, если последова-тельность ν или последовательность ν-1 является подпоследовательностью последовательности μ. В ориентированном случае остаётся только часть этого определения: не циклический орпуть νсодержится в не циклическом пути орпути μ, если последовательность ν является подпоследо-вательностью последовательности μ.
Для циклических путей последнее определение требуется модифицировать, учитывая то, что такой путь можно «обходить», начиная с любой вершины, отчего он, конечно же, не изме-нится. Поэтому можно дать такие четыре определения:
1) не циклический путь ν содержится в циклическом пути μ, если последовательность μ можноциклически перенумеровать так, что последовательность νили последовательность ν-1 станет подпоследовательностью этой перенумерованной последовательности μ;
2) не циклический орпуть ν содержится в циклическом орпути μ, если последовательность μ можноциклически перенумеровать так, что последовательность ν станет подпоследователь-ностью этой перенумерованной последовательности μ;
3) циклический путь ν содержится в пути μ, если последовательность νили последова-тельность ν-1 можноциклически перенумеровать так, что эта перенумерованная последователь-ность ν станет подпоследовательностью последовательности μ;
4) циклический орпуть ν содержится в орпути μ, если последовательность ν можноцикли-чески перенумеровать так, что эта перенумерованная последовательность ν станет подпоследо-вательностью последовательности μ.
Эти на первый взгляд сложные понятия разъясняются далее (см. пример 13).
Все вышеприведённые в данном разделе понятия относятся к произвольным графам и ор-графам (см. раздел 1.1). В случае простых графов и орграфов понятие пути (орпути) упрощает-ся: под путём (орпутём) понимается последовательность вершин
μ =áv0, v1, ..., vk-1,vkñ, (5)
такая, что множество вершин {vi , vi+1} определяет ребро графа (петлю, если vi и vi+1 совпадают)
(пара вершин ávi , vi+1ñ определяет дугу орграфа (петлю, если vi и vi+1 совпадают)). Напомним, что в простых графах (орграфах) пара вершин однозначно определяет ребро (дугу), в то время как в графах общего вида таких рёбер (дуг) может быть несколько (см. рис.3, а также рис.5.1 и
10.1). Соответственно упрощаются все остальные приведённые выше определения – достаточно указывать только последовательности вершин.
Приведём примеры, иллюстрирующие и разъясняющие введённые понятия.
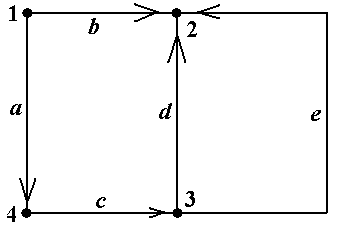
Пример 10. В графе, показанном на рис.11 (копия рис.5-6), обратным к пути μ = á1, f, 4, d, 2, c, 4, g, 3ñ является путь μ-1= á3, g, 4, c, 2, d, 4, f, 1ñ. Обратным к циклическому пути μ =á1, f, 4, d, 2, e, 3, b, 1ñ является циклический путь μ-1 = á1, b, 3, e, 2, d, 4, f, 1ñ (проверьте!) ■
Пример 11.В графе, показанном на рис.12 (копия рис.5-7), обратным к простому пути μ = á2, 1, 4, 3ñ является путь простой путь μ-1 = á3, 4, 1, 2ñ. Обратным к циклическому пути μ-1 = á2, 4, 1, 3, 4, 2ñ является циклический путь μ-1 = á2, 4, 3, 1, 4, 2ñ■
Пример 12. В графе, показанном на рис.13 (копия рис.5-3) последовательность μ = á1, d, 3,
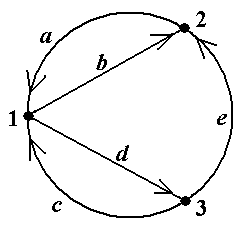
e, 2, b, 1, a, 2, b, 1, c, 3ñ является путём с началом в вершине 1 и концом в вершине 3. Его длина, т.е. число входящих в него рёбер, равно 6. Этот путь не является цепью, так как не все его рёбра различны (ребро b встречается два раза). В этом же графе последовательность ν = á1, d, 3, e, 2, b, 1, c, 3ñ является цепью с началом в вершине 1 и концом в вершине 3. Эта цепь не является простой, так как в ней не все вершины различны (вершины 1 и 3 встречаются по два раза). По-следовательность λ = á1, d, 3ñ является простой цепью. Последовательность λ* = á1, c, 3ñ также является простой цепью, отличной от простой цепи λ = á1, d, 3ñ (см. рис.13). Заметим, что все четыре рассмотренных в примере пути μ, ν, λ, λ* соединяют одну и ту же пару вершин 1 и 3 ■
Пример 13. Граф, показанный на рис.14 (копия рис.7-c) является простым графом, поэто-му для задания путей можно пользоваться упрощёнными последовательностями, состоящими
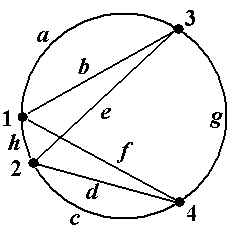 Рис.11 Рис.11 |  Рис.12 Рис.12 |
только из вершин. Последовательность μ = áD, C, G, E, C, B, G, E, Fñ является путём с началом в
вершине D и концом в вершине F; его длина равна 8. Путь μ не является цепью, так как ребро {G, E} входит в него дважды. Последовательность ν = áD, C, G, E, C, B, Fñ является цепью, так как все её рёбра не повторяются (проверьте!), но она не является простой цепью, так как вершина Cвстречается в ней два раза. Последовательность λ = áD, C, B, Fñ является простой цепью, поскольку все её вершины различны. Заметим, что все три рассмотренные пути – μ, ν, λ – соединяют одну и ту же пару вершин D и F ■
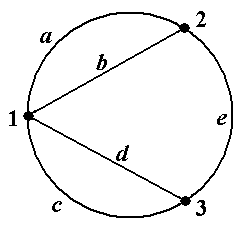 Рис.13 Рис.13 | 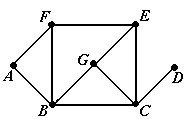 Рис.14 Рис.14 |
Замечания в конце примеров 12 и 13 приводят к достаточно простому умозаключению, сформулированному в следующем утверждении.
Утверждение 6. Для всякого пути (орцепи), соединяющего две разные вершины, есть содержащаяся в нём цепь (орцепь), соединяющая те же две вершины. Для всякой цепи (орцепи), соединяющей две вершины, есть содержащаяся в ней простая цепь (орцепь), соединяющая те же две вершины ■
Заметим, что существующая в силу утверждения 6 цепь может совпадать с содержащим её путём (если сам путь уже является цепью); существующая в силу утверждения 6 простая цепь может совпадать с содержащей её цепью (если сама эта цепь уже является простой цепью).
Пример 14. В графе, показанном на рис.15 (копия рис.5-15) последовательность μ = á1, a, 2, b, 1, a, 2ñ является путём. Этот путь не является цепью, поскольку он проходит два раза по ребру a. Двумя содержащимися в этом пути цепями являются только цепи ν = á1, a, 2ñ и ν* = á1, b, 2ñ. Обе эти цепи уже являются простыми, и поэтому любая содержащаяся в одной из них простая цепь совпадает с содержащей цепью ■
Заметим также, что во всех рассмотренных в примерах 12 − 14 путях начальная и конеч-ная вершины всегда различны, т.е. ни один из них не является циклическим путём.
Задание 4.Вграфах, показанных на рис.5, найти
1) путь, не являющийся цепью;
2) содержащуюся в найденном в 1) пути цепь, не являющуюся простой, соединяющую те же самые вершины;
3)содержащуюся в найденной в 2) цепи простую цепь, соединяющую те же самые верши-ны.
Если некоторые искомые объекты не существуют (как в примере 14), то объяснить это ■
Задание 5.Вграфах, показанных на рис.7, найти
1) путь, не являющийся цепью;
2) не содержащуюся в найденном в 1) пути цепь, не являющуюся простой;
3) не содержащуюся в найденной в 2) цепи простую цепь.
Если некоторые искомые объекты не существуют, то объяснить это ■
Пример 15.Рассмотрим простой граф, показанный на рис.16 (копия рис.5-9). Не цикли-
ческий путь μ = á6, 2, 5ñ содержится в циклическом пути ν = á2, 5, 3, 6, 2ñ, хотя последователь-ность μ не является подпоследовательностью последовательности ν. Действительно, если тот же самый циклический путь ν начать с вершины 6, т.е. записать в виде ν = á6, 2, 5, 3 ,6ñ, то после такой перенумерации последовательность μ становится подпоследовательностью последова-тельности ν. Рассмотрим теперь не циклический путь μ = á4, 1, 5ñ и циклический путь ν = á1, 4, 2, 5, 1ñ. Последовательность á4, 1, 5ñне является подпоследовательностью ни самой последова-тельности ν,ни любой её циклической перестановки: á4, 2, 5, 1, 4ñ, á2, 5, 1, 4, 2ñ, á5, 1, 4, 2, 5ñ. Однако обратная последовательность μ-1= á5, 1, 4ñ содержится в циклически переставленной ν = á4, 2, 5, 1, 4ñ, и, значит, в силу введённых определений, путь μ = á4, 1, 5ñ содержится в цикли-ческом пути ν ■
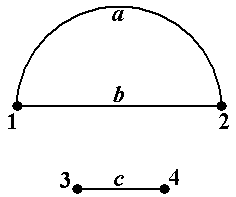 Рис.15 Рис.15 | 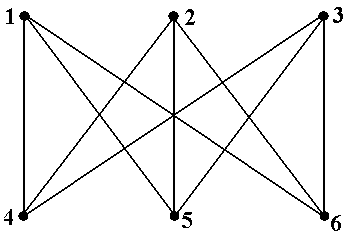 Рис.16 Рис.16 |
Пример 16. В графе, показанном на рис.13, последовательность μ = á1, d, 3, е, 2, е, 3, с, 1, b, 2, a, 1ñ является циклическим путём, но не является циклом, поскольку ребро е входит в него дважды. Содержащийся в пути μ путь ν = á1, d, 3, с, 1, b, 2, a, 1ñ является циклом, но не является простым циклом, так начальная и конечная вершина 1 входит в него 3 раза, вместо двух, требу-емых определением. Наконец, содержащийся в пути ν путь λ = á1, d, 3, с, 1ñ является простым циклом ■
Пример 17.В графе, показанном на рис.14, последовательность μ = áE, C, G,B, A, F, B, G, Eñ является циклическим путём, но не является циклом, поскольку ребро {G,B} входит в него дважды. Содержащийся в пути μ путь ν = áE, C, B, A, F, B, G, Eñ является циклом, но не является простым циклом, так вершинаB входит в него 2 раза. Наконец, содержащийся в пути ν путь λ = áE, C, B, G, Eñ является простым циклом ■
Имеет место утверждение, аналогичное утверждению 7 для не циклических путей.
Утверждение 7. Для всякого циклического пути (орпути) есть содержащийся в нём цикл (орцикл). Для всякого цикла (орцикла) есть содержащийся в нём простой цикл (орцикл) ■
Задание 6.Вграфах, показанных на рис.5, найти
1) циклический путь, не являющийся циклом;
2) содержащийся в найденном в 1) пути цикл, не являющийся простым;
3) содержащийся в найденном в 2) цикле простой цикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
Задание 7.Вграфах, показанных на рис.7, найти
1) циклический путь, не являющийся циклом;
2) не содержащийся в найденном в 1) пути цикл, не являющийся простым;
3) не содержащийся в найденном в 2) цикле простой цикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
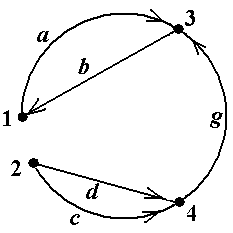
Пример 18.В орграфе, показанном на рис.17 (копия рис.10-3) последовательность μ = á1, b, 2, a, 1, d, 3, c, 1ñ является циклическим орпутём, который является орциклом. Этот орцикл содержит два простых цикла: ν1 = á1, b, 2, a, 1ñ и ν2 =á 1, d, 3, c, 1ñ. Кроме них, в данном орграфе есть простой орцикл á1, d, 3, e, 2, a, 1ñ■
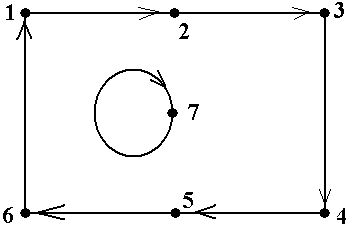
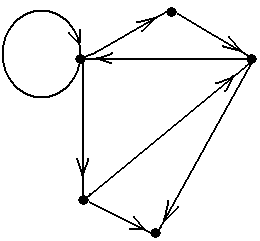
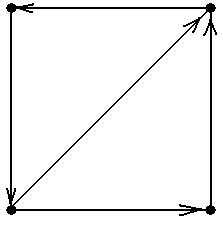
Пример 19.В орграфе, показанном на рис.18 (копия рис.10-4) имеется два орцикла: á1, 2, 3, 4, 5, 6, 1ñ и á7, 7ñ. Они оба являются простыми орциклами ■
 Рис.17 Рис.17 |  Рис.18 Рис.18 |
Задание 8.Ворграфах, показанных на рис.10, найти
1) циклический орпуть, не являющийся орциклом;
2) содержащийся в найденном в 1) орпути орцикл, не являющийся простым;
3) содержащийся в найденном в 2) орцикле простой орцикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
Задание 9.Ворграфах, показанных на рис.10, найти
1) циклический орпуть, не являющийся орциклом;
2) не содержащийся в найденном в 1) пути орцикл, не являющийся простым;
3) не содержащийся в найденном в 2) орцикле простой орцикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
Введём ещё одно важное для дальнейшего понятие. Граф (орграф) называется ациклич-ным, если он не содержит циклов (орциклов). Рассмотрим подробнее ацикличные орграфы. В ацикличном орграфе по самому определению отсутствуют орциклы и, следовательно, все орпу-ти являются простыми. Однако для ацикличных орграфов верен и более специальный факт, в каком-то смысле описывающий их структуру. Имеет место
Утверждение 8. Пусть G(V, A) – простой ацикличный граф с множеством вершин Vи множеством дуг A. Тогда множество вершин Vразбивается на непересекающиеся подмножест-ва V1, …, Vm, такие, что для любой дуги (p, q) графа Gначало p содержится в множестве Vic бóльшим номером, чем конец q.
Доказательство этого утверждения, по сути, является алгоритмом построения указанных подмножеств. Поскольку граф ацикличен, то в нём найдётся хотя бы одна дуга, из которой не выходят дуги. Обозначим множество всех таких вершин через V1. Удалим из графа G все вер-шины из V1 и все ведущие в них дуги. Оставшийся граф также будет ацикличным. Множество его вершин, из которых не выходят дуги, обозначим через V2. Продолжая этот процесс, полу-чим разбиение с требуемыми свойствами (последний оставшийся граф Gm не может содержать дуг, иначе на нём процесс не мог бы окончиться) ■
