Развязка индуктивных связей

Выше было сказано, что не все методы пригодны для расчета индуктивно связанных цепей. Анализ и расчет цепи упрощается, если часть цепи содержащую индуктивные связи заменить эквивалентной схемой без индуктивных связей. Эта замена является называется развязкой индуктивных связей.

Рассмотрим часть цепи с индуктивной связью (рис 5.11)

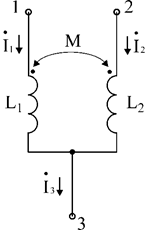
Рис 5.11

Запишем для нее уравнения в комплексной форме

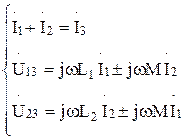
где знак (+) перед 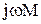соответствует согласному включению индуктивностей, а знак (–) встречному. Выразив из первого уравнения ток 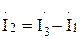и подставив в выражение для 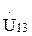, получим

, а выразив

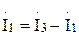и подставив в , получим:

.

Полученным уравнениям для 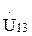и соответствует электрическая цепь, изображенная на рис 5.12

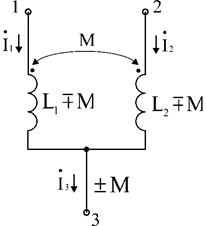
Рис 5.12

В цепи на рис 5.12 отсутствует индуктивные связи, однако изменились величины индуктивностей и появился дополнительный элемент. Верхний знак перед М соответствует согласному включению, а нижний знак –встречное включение индуктивностей.

Для расчета цепи преобразованной таким образом можно использовать любые методы расчета цепей без ограничения.

Воздушный трансформатор

Трансформатор слово латинского происхождения и переводится как преобразователь. Этим определяется его назначение. Трансформатор служит для преобразования переменного напряжения, когда требуется изменить величину напряжения или осуществить передачу электрической энергии между контурами лишенными гальванической связи.

Конструктивно трансформатор представляет собой две или несколько индуктивно связных катушек, называемых обмотками трансформатора. Обмотки трансформатора могут быть помещены на общий ферромагнитный сердечник. Однако сердечник может отсутствовать. Тогда трансформатор называется воздушным трансформатором или трансформатором без сердечника.

Рассмотрим простейший воздушный трансформатор, состоящий из 2-х обмоток.

Такие трансформаторы находят широкое применение в устройствах работающих на высоких частотах, например, в радиоприемных устройствах. Схема трансформатора представлена на рис 5.13

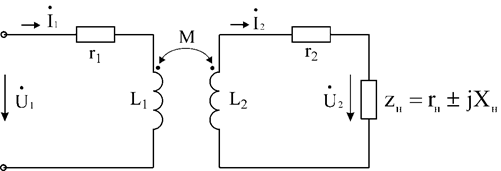
Рис 5.13

Обмотка трансформатора, подключаемая к источнику переменного напряжения, называется первичной. На рис 5.13 она представлена индуктивностью L₁ и активным сопротивлением проводника r₁, из которого она изготовлена. Вторичная обмотка, к которой подключается нагрузка Z_Н, представлена индуктивностью L₂ и активным сопротивлением r₂. Между обмотками трансформатора имеется индуктивная связь, характеризуемая взаимной индуктивностью M.

Уравнения по второму закону Кирхгофа для первичной и вторичной цепи трансформатора запишутся в виде:

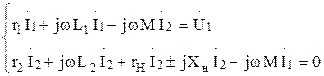
Векторные диаграммы трансформатора для случаев активно-индуктивной 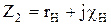и активно-емкостной 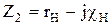нагрузки, построенные по уравнениям приведены на рис. 5.14 а, б соответственно :

Рис. 5.14

Порядок построения векторной диаграммы трансформатора проследим на рисунке 5.14а. Зададимся положительным направлением тока во вторичной обмотке трансформатора. Напряжение на активном сопротивлении вторичной обмотки трансформатора совпадает по фазе стоком . Напряжение на индуктивности вторичной катушки опережает ток на 90⁰. Совмещаем начало вектора концом вектора 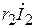. Напряжение на активной составляющей сопротивления нагрузке совпадает по фазе с током . Откладываем вектор параллельно вектору тока с конца вектора . Вектор напряжения на индуктивной составляющей сопротивления нагрузки опережает ток на 90⁰, откладываем с конца вектора под углом 90⁰ к вектору . Векторная сумма равна вектору напряжения 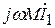, возникающего за счёт индуктивной связи между первичной и вторичной катушками. Вектор тока 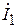относительно 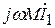сдвинут на –90⁰. Определив таким образом направление тока 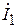строим векторы напряжений на элементах первичной цепи трансформатора согласно первому уравнению трансформатора.

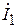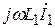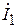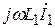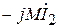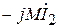Вектор напряжения на активном сопротивлении первичной катушки совпадает с током . Вектор напряжения на индуктивности первой катушки опережает ток на 90⁰. Совмещаем начало вектора с концом вектора . Падение напряжения , вызванное в первичной цепи током вторичной цепи имеет сдвиг фазы – 90⁰ по отношению к току . Откладываем вектор с конца вектора 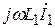под углом –90⁰ к току . Сумма векторов даёт вектор входного напряжения трансформатора .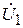

Определим входное сопротивление трансформатора. Уравнения описывающие воздушный трансформатор запишем в виде

где -- реактивное сопротивление первичной цепи

-- активное сопротивление вторичной цепи

-- реактивное сопротивление вторичной цепи трансформатора. Из системы уравнений определим ток.

Разделим числитель и знаменатель последнего выражения на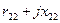

Полученное соотношение

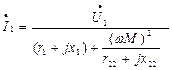
выражает закон Ома для первичной цепи. Следовательно, знаменатель представляет собой выражение для входного сопротивления трансформатора.

Выделим в выражении для входного сопротивления трансформатора действительную и мнимую часть, умножив числитель и знаменатель третьего слагаемого на число комплексно - сопряженное знаменателю

Таким образом, входное сопротивление трансформатора представлено в виде последовательного соединения двух активных и двух реактивных сопротивлений. Входное сопротивление трансформатора может быть изображено в виде двухполюсника на рис 5.15

Рис 5.15

где 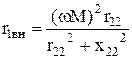активное сопротивление, вносимое из вторичной цепи в первичной.

x_1вн= реактивное сопротивление, вносимое в первичную цепь из вторичной .

Следует заметить, что вносимое реактивное сопротивление имеет знак противоположный знаку собственного реактивного сопротивления вторичного контура x₂₂.

Из представления воздушного трансформатора в виде двухполюсника следует условие передачи максимальной мощности в нагрузку Z_ист=Z_H^*.

Другой подход к анализу трансформатора предполагает исключение индуктивной связи между обмотками и получения эквивалентной схемы замещения трансформатора.

Запишем уравнения трансформатора в виде

Добавим и вычтем к левой части первого уравнения слагаемое 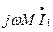, а к левой части второго уравнения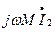

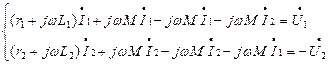
Преобразуем полученные уравнения

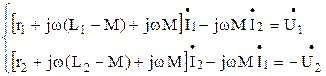
Из последних уравнений следует, что цепь описываемая ими состоит из 2-х контуров, имеющих общее сопротивление 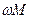. В первом контуре протекает ток 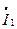во втором – ток . Схема цепи , описываемая этими уравнениями приведена на рис 5.16

Рис 5.16

Полученная схема цепи может рассматриваться как эквивалентная исходной в отношении напряжений и 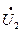и токов 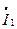и .

Как отмечалось выше, основное назначение трансформатора – повышение или понижение в некоторое число раз напряжения и тока. В идеальном случае такое преобразование не должно завесить ни от частоты приложенного напряжения ни от величины нагрузки. Рассмотрим ,при каких условиях это возможно.

Введём понятия функции передачи тока и функции передачи напряжения, и , соответственно.

Из второго уравнения системы 5.1 выразим .

Разделив левую и правую части полученного соотношения на 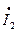получим

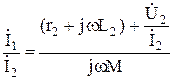
Из последнего выражения с учётом , получим функцию передачи тока.

Функцию передачи напряжения получим как отношение второго уравнения к первому из системы 5.1

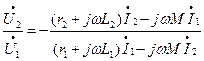
Разделив числитель и знаменатель последнего выражения на 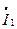, получим соотношение

включающее в себя функцию передачи тока 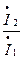.Подставив значение 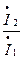, окончательно получим функцию передачи напряжения в виде

Как следует из выражений для функции передачи тока и напряжения, они зависят от многих величин.

Если можно пренебречь потерями в обмотках трансформатора, т. е. если r₁=r₂=0, то функция передачи напряжения запишется в виде

Полагая, что потоки рассеяния отсутствуют, т.е. коэффициент связи , получим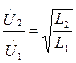

Индуктивность обмотки трансформатора пропорциональна квадрату витков обмотки , где -магнитная проводимость пути, по которому протекает поток.

Выразив величины индуктивносте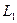й и 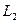через число витков 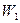и , получим функцию передачи напряжения в виде

Отношение назовем коэффициентом трансформации и обозначим буквой n.

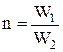
Таким образом независимость от частоты и нагрузки функции передачи напряжения обеспечивается при нулевом активном сопротивлении и коэффициенте связи .

Рассмотрим условие независимости от частоты функции передачи тока

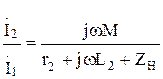
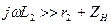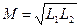Если индуктивное сопротивление вторичной цепи значительно больше сопротивления нагрузки и активного сопротивления и , , то

Идеальным трансформатором называется идеализированный элемент электрической цепи с двумя парами зажимов –первичных и вторичных , обладающий следующими свойствами : при любых условиях отношение первичного и вторичного комплексных токов равны постоянному числу

n-коэффициенту трансформации.

Если n>1, то трансформатор называется понижающим, если n<1, то трансформатор – повышающий.

Рассмотрим свойства идеального трансформатора.

Пусть ко вторичным зажимам подключена нагрузка с комплексным сопротивлением 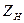. Тогда входное сопротивление будет равным :

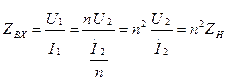
Т.е входное сопротивление изменилось в n² раз. Это позволяет применять трансформатор для согласования источника и нагрузки , например, по условию передачи в нагрузку максимальной мощности .

Например, если сопротивление источника равно r_i, а сопротивление нагрузки – r_H, то входное сопротивление относительно первичной обмотки равно 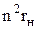и условие согласования запишется в виде

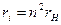откуда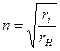

Установим связь между мощностью на входе и выходе идеального трансформатора.

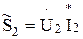–мощность на входе трансформатора

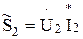–мощность на выходе трансформатора

Таким образом, идеальный трансформатор передает энергию с входа на выход цепи без потерь.

Сформулируем условия, которые должны выполнятся для того, что бы трансформатор был идеальным:

1.Должны отсутствовать потоки рассеяния, т. е .

2. Должны отсутствовать потери, т.е

3. Должны быть великими индуктивности обмоток, т.е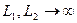

Реальные трансформаторы могут обеспечить выполнение условий лишь приближенно за счет технических решений:

1. Для отсутствия потока рассеяния обмотки трансформатора помещают на замкнутом сердечнике , выполненном из материала с высокой магнитной проводимостью.

2. Второе условие обеспечивает выбором обмоточного проводника , обладающего низким удельным сопротивлением .

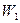3. Для выполнения условия , обмотки должны иметь большое число витков и и высокую магнитную проводимость материала сердечника.

По своим свойствам к идеальному трансформатору приближается трансформатор с ферромагнитным сердечником . Трансформатор с ферромагнитным сердечником может рассматриваться как линейный элемент , если магнитный поток не насыщает сердечника . Это условие обычно выполняется за исключением приборов , где насыщение принципиально необходимо.

Практический раздел