Задания для самостоятельного выполнения. Решить задачу о школьном кондитерском цехе, рассмот­ренную в новой постановке

Задание 1

Решить задачу о школьном кондитерском цехе, рассмот­ренную в новой постановке. Пусть цех производит четыре вида продукции:

‒ пирожки (максимально возможно произвести 2000 штук в день, если ничего больше не производить);

‒ шанежки (максимальный выпуск 1500 штук в день);

‒ булочки (максимальный выпуск 1200 штук в день);

‒ пирожные (максимальный выпуск 700 штук в день).

Соотношение стоимости изделий таково:

‒ пирожок/булочка — 2/1;

‒ пирожок/шанежка — 1/2;

‒ пирожок/пирожное —1/4.

Емкость склада равна 1100 изделий независимо от их вида.

Составить оптимальный план выпуска продукции исходя из той же цели — достижения максимальной выручки цеха. При решении задачи использовать средство Excel «Поиск решения».

Задание 2

Составить оптимальный план проведения экскурсионных поездок школьников во время каникул в следующей ситуации. Областной департамент образования может профинансировать поездки школьников из пяти районов области (районы будем обозначать номерами) в три города (назовем эти города X, Y и Z).

Количество учащихся, которых следует отправить в поезд­ки, таково:

Номер района
Количество экскурсантов

Экскурсионное бюро может в данные каникулы обеспечить поездку следующего числа учащихся в каждый из этих городов:

Город	X	Y	Z
Количество экскурсантов

Стоимость (в рублях) поездки одного учащегося из райо­нов в города приведена в следующей таблице.

Города	Стоимость поездок из районов
X
Y
Z

Смысл чисел в таблице таков: если в ячейке Y2 стоит 600, то это значит, что поездка одного учащегося из района 2 в город Y обходится в 600 рублей.

Необходимо составить такой план экскурсий, который:

1) позволяет каждому из числа намеченных к поездке учащихся побывать на экскурсии;

2) удовлетворяет условию, определяющему общее число экскурсантов, едущих в каждый из городов;

3) обеспечивает максимально низкие суммарные расходы финансирующей стороны.

Математическая формулировка.План перевозок, который нам надлежит составить, будет отражен в следующей таблице:

Города	Количество учащихся, едущих из районов
X	x1	x2	x3	x4	x5
Y	y1	y2	y3	y4	y5
Z	z1	z2	z3	z4	z5

Итак, мы имеем все для полной математической форму­лировки задачи: требуется найти наименьшее значение фун­кции (4) при условии, что входящие в нее переменные удов­летворяют системам уравнений (1) и (2) и неравенств (3).

Это — весьма непростая задача. Однако ее вполне можно решить (как и существенно более сложные задачи) с помо­щью средств «Поиск решений» программы Excel, которым вам и надлежит воспользоваться.

Приведем результат решения этой задачи:

Величины, стоящие в этой таблице, и являются объектами поиска. Так, х3 есть число учащихся из района № 3, ко­торые, по разрабатываемому плану поедут в город X.

Первое условие (ограничение задачи) состоит в том, что все учащиеся из каждого района поедут на экскурсию. Ма­тематически оно выражается следующими уравнениями:

x1 + y1+ z1 = 300

x2+y2+z2 = 250,

x3+y3+z3 = 400, (1)

х4 + у4 + z4 = 350,

x5+y5+z5 = 200.

Второе условие: в каждый город поедут столько учащих­ся, сколько этот город в состоянии принять:

х1 + х2 + х3 + х4 + х5 = 400,

y1+y2+y3+y4+y5 = 500, (2)

z1+z2+z3+z4+z5 = 600.

Кроме того, искомые величины, разумеется, неотрицате­льны:

х1 > 0,..., х5 > 0, у1 > 0,..., у5 >0, z1> 0,..., z5 > 0. (3)

Теперь запишем общую стоимость расходов на экскурсии. Поскольку привезти, например, на экскурсию хг учащихся стоит х1 • 500 рублей (см. таблицу стоимости поездки), то общие расходы составят

S = x1 • 500 + х2 • 700 + х3 • 750 + х4 • 1000 +

+ х5 • 1100 + y1• 700 + у2 • 600 + y3 • 400 +

+ y4 • 500 + y5 • 800 + z1• 1200 + z2 • 1000 +
+ z3 • 800 + z4 • 600 + z5 • 500 (4).

x1

x2

x3

x4

x5

y1

y2

y3

y4

y5

z1

z2

z3

z4

z5

Итак, в город X поедут на экскурсию 300 учащихся из района № 1 и 100 учащихся из района № 2, в город У — 100 учащихся из района № 2 и 400 из района № 3, в город Z — 50 учащихся из района № 2, 350 из района № 4 и 200 — из района № 5.

Или скажем то же самое по другому: все учащиеся из района № 1 уедут в город X, учащиеся из района № 2 поде­лятся между городами X, Y и Z (соответственно 100, 100 и 50), все учащиеся из района № 3 уедут в город Y, а все уча­щиеся из районов № 4 и № 5 поедут в город Z. Такое неоче­видное разделение обеспечивает в данном случае наиболь­шую экономию средств.

Вопросы и задания

1) В чем состоит задача оптимального планирования?

2) Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.

3) Попробуйте сформулировать содержание оптимального планирования своей учебной деятельности.

4) Что такое математическое программирование, линейное программирование?

5) Сформулируйте задачу оптимального планирования для того же школьного кондитерского цеха, в котором выпускается три вида продукции: пирожки, пирожные и ковржики.

6) Внесите изменение в постановку рассмотренной задачи оптимального планирования для двух видов продукции с учетом еще одного условия ограничения: число пирожных должно быть не меньше числа пирожков. На координатной плоскости постройте область поиска решения.

Общие положения

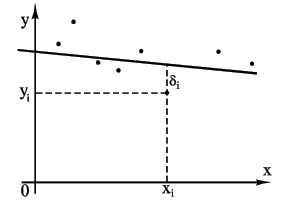Для упрощения изложения рассмотрим сначала случай линейной функции одного аргумента. Пусть из опыта получены точки:

x1, y1,
x2, y2, ...		(1)
xn, yn

(см. рисунок). Требуется найти уравнение прямой

y=ax+b,

(2)

наилучшим образом согласующейся с опытными точками.

Пусть мы нашли такую прямую. Обозначим через 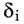расстояние опытной точки от этой прямой (измеренное параллельно оси y).

Из уравнения (2) следует, что

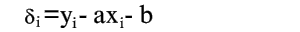(3)

Чем меньше числа 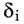по абсолютной величине, тем лучше подобрана прямая (2). В качестве характеристики точности подбора прямой (2) можно принять сумму квадратов

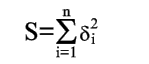(4)

Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем

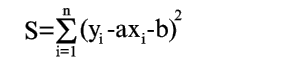(5)

Условия минимума S будут

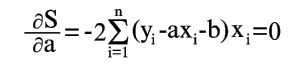	(6)
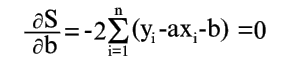	(7)

Уравнения (6) и (7) можно записать в таком виде:

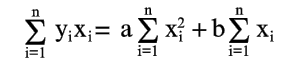	(8)
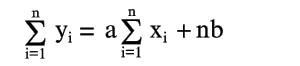	(9)

Из уравнений (8) и (9) легко найти a и b по опытным значениям x_i и y_i. Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями.

Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b

y1=ax1+b,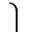
y2=ax2+b, ...		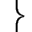(10)
yn=axn+b,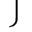

Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x₁, x₂, ..., x_n) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8).

Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9).

Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции

y=a0+a1x+a2x2+...+anxn.

(11)

Естественно, что здесь получится система из n+1 нормального уравнения для определения величин
a₀, a₁, a₂, ..., a_n.

Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что

k=y/x

(12)

есть величина постоянная и ее нужно определить по опытным данным (1).

Систему уравнений для k можно записать:

k=y1/x1,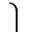
k=y2/x2, ...		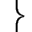(13)
k=yn/xn,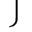

Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т.е. на 1, и сложим полученные уравнения

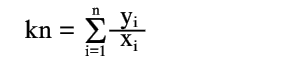(14)

отсюда

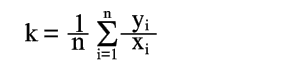(15)

Следовательно, среднее арифметическое, полученное из опытных отношений y_i/x_i, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных.

Пример 1

На опыте получены значения x и y, сведенные в таблицу

x
y	5,2	6,3	7,1	8,5	9,2	10,0

Найти прямую (2) по методу наименьших квадратов.

Решение. Находим:

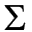x_i=21, 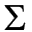y_i=46,3, 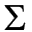x_i²=91, 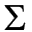x_iy_i=179,1.

Записываем уравнения (8) и (9)

91a+21b=179,1,

21a+6b=46,3,

отсюда находим

a=0,98 b=4,3.

Линейная регрессия. Использование метода наименьших квадратов (МНК)

Выбрав вид функции регрессии, т.е. вид рассматриваемой модели зависимости Y от Х (или Х от У), например, линейную модель y_x=a+bx, необходимо определить конкретные значения коэффициентов модели.

При различных значениях а и b можно построить бесконечное число зависимостей вида y_x=a+bx т.е на координатной плоскости имеется бесконечное количество прямых, нам же необходима такая зависимость, которая соответствует наблюдаемым значениям наилучшим образом. Таким образом, задача сводится к подбору наилучших коэффициентов.

Линейную функцию a+bx ищем, исходя лишь из некоторого количества имеющихся наблюдений. Для нахождения функции с наилучшим соответствием наблюдаемым значениям используем метод наименьших квадратов.

Обозначим: Y_i - значение, вычисленное по уравнению Y_i=a+bx_i. y_i - измеренное значение, ε_i=y_i-Y_i - разность между измеренными и вычисленными по уравнению значениям, ε_i=y_i-a-bx_i.

В методе наименьших квадратов требуется, чтобы ε_i, разность между измеренными y_i и вычисленными по уравнению значениям Y_i, была минимальной. Следовательно, находим коэффициенты а и b так, чтобы сумма квадратов отклонений наблюдаемых значений от значений на прямой линии регрессии оказалась наименьшей:

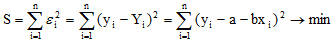
Исследуя на экстремум эту функцию аргументов а и с помощью производных, можно доказать, что функция принимает минимальное значение, если коэффициенты а и b являются решениями системы:

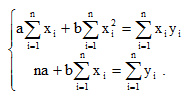(2)

Если разделить обе части нормальных уравнений на n, то получим:

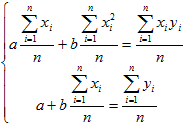
Учитывая, что 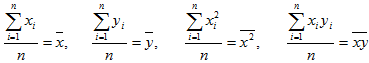(3)

Получим 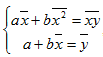, отсюда 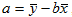, подставляя значение a в первое уравнение, получим:

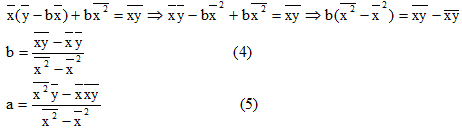
При этом b называют коэффициентом регрессии; a называют свободным членом уравнения регрессии и вычисляют по формуле: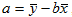

Полученная прямая является оценкой для теоретической линии регрессии. Имеем:

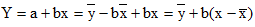
Итак, 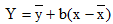является уравнением линейной регрессии.

Регрессия может быть прямой (b>0) и обратной (b<0). Прямая регрессия означает, что при росте одного параметра, значения другого параметра тоже увеличиваются. А обратная, что при росте одного параметра, значения другого параметра уменьшаются.

Пример 1. Результаты измерения величин X и Y даны в таблице:

xi	-2
yi	0.5		1.5

Предполагая, что между X и Y существует линейная зависимость y=a+bx, способом наименьших квадратов определить коэффициенты a и b.

Решение. Здесь n=5
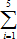x_i=-2+0+1+2+4=5;
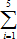x_i²=4+0+1+4+16=25
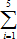x_iy_i=-2•0.5+0•1+1•1.5+2•2+4•3=16.5
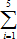y_i=0.5+1+1.5+2+3=8

и нормальная система (2) имеет вид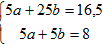

Решая эту систему, получим: b=0.425, a=1.175. Поэтому y=1.175+0.425x.

Пример 2. Имеется выборка из 10 наблюдений экономических показателей (X) и (Y).

xi
yi

Требуется найти выборочное уравнение регрессии Y на X. Построить выборочную линию регрессии Y на X.

Решение. 1. Проведем упорядочивание данных по значениям x_i и y_i. Получаем новую таблицу:

xi
yi

Для упрощения вычислений составим расчетную таблицу, в которую занесем необходимые численные значения.

xi	yi	xi2	xiyi
∑xi=1729	∑yi=1761	∑xi2299105	∑xiyi=304696
x=172.9	y=176.1	xi2=29910.5	xy=30469.6

Согласно формуле (4), вычисляем коэффициента регрессии

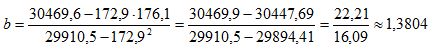
а по формуле (5)

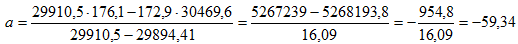
Таким образом, выборочное уравнение регрессии имеет вид y=-59.34+1.3804x.
Нанесем на координатной плоскости точки (x_i; y_i) и отметим прямую регрессии.

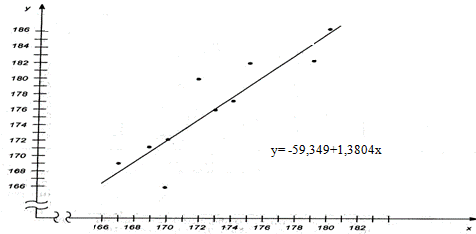
Рис 4

На рис.4 видно, как располагаются наблюдаемые значения относительно линии регрессии. Для численной оценки отклонений y_i от Y_i, где y_i наблюдаемые, а Y_iопределяемые регрессией значения, составим таблицу:

xi	yi	Yi	Yi-yi
		168.055	-0.945
		170.778	-0.222
		172.140	6.140
		172.140	0.140
		174.863	-5.137
		176.225	0.225
		177.587	0.587
		178.949	-3.051
		184.395	2.395
		185.757	-0.243

Значения Y_i вычислены согласно уравнению регрессии.

Заметное отклонение некоторых наблюдаемых значений от линии регрессии объясняется малым числом наблюдений. При исследовании степени линейной зависимости Y от X число наблюдений учитывается. Сила зависимости определяется величиной коэффициента корреляции.