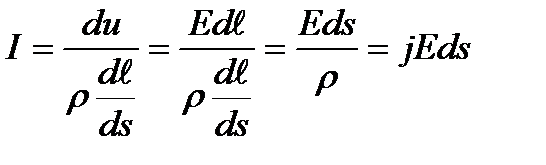Потенциал градиенті

Градиент деп –берілген потенциалдың басқа нүктемен салыстырғандағысына айтылады. Сонда элкетростатикалық өрістің потенциалы нүктеден нүктеге өзгеретін функция болып табылады.

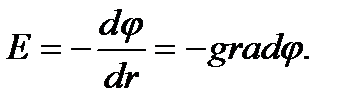
Мұндағы минус таңба q¹ нүктелік зарядты q зарядын қашықтатып көшірілген нүктедегі потенциалдың бірте –бірте кеміп баруын көрсетеді. Сонда Е – кернеулік кері таңбамен алынған потенциалдың градиентіне тең болады. Кернеулік бет бойынша Остроградский-Гаусс теоремасы бойынша таралады. Мұнда кез – келген тұйық беттен өтетін электрлік ығысу ағынының сол беттің ішіндегі электр зарядының арасындағы байланысты көрсететін теорема. Сонда,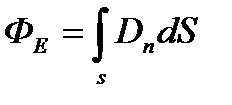

Өрістің берілген нүктесіндегі өріс потенциалы деп аталатын

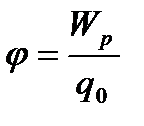
скалярлық шама, 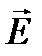кернеулік векторымен қоса, электр өрісін сипаттау үшін пайдаланылады. Сонда зарядты 1-ші нүктеден 2-шіге орын ауыстырғандағы электростатикалық өріс күштерінің атқаратын жұмысын мына түрде жазуға болады

.

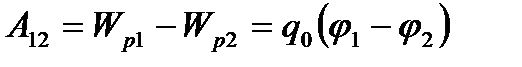Электростатикалық өрістің 1 және 2 нүктелерінің потенциалдар айырмасы бірлік оң зарядты 1-ші нүктеден 2-шіге орын ауыстырғандағы өріс күштерінің атқаратын жұмысына тең:

.

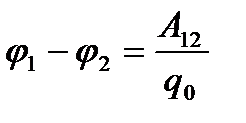Потенциалдың өлшем бірлігі – вольт (В): 1Кл зарядтың 1Дж потенциалдық энергияны иеленетін өріс нүктесінің потенциалы 1В-қа тең деп алынады.

Зарядтар жүйесінің өріс потенциалыәр жеке зарядтың туғызатын өріс потенциалдарының алгебралық қосындысына тең:

.

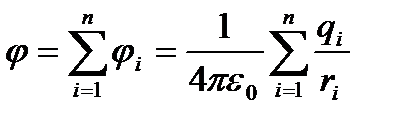Электростатикалық өрістің кернеулік векторының кез келген тұйық контур бойымен алынған циркуляциясы нөлге тең.

Электростатикалық өріс кернеулігі мен потенциал арасындағы байланыс мына теңдеумен өрнектеледі:

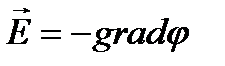немесе .

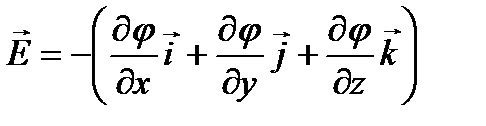Барлық нүктелеріндегі потенциалдың мәндері бірдей беттерді эквипотенциалды беттер деп атайды.

Эквипатенциал беттердің қасиеттері:

1. Егер нүктелік заряд эквипатенциал беттің бойымен орын ауыстырса оның істеген жұмысы нолге тең болады.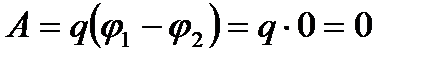

2. Өріс кернеулігінің күш сызықтары әр уақытта эквипатенциал бетке нормаль болады. Егер ондай болмаса онда элкетр өрісі кернеулігі тангенциал немесе жанама болып атқарған жұмысы нолден өзгеше болады.

3. Электростатикалық өрістегі электр өткізгішінің беті әр уақытта эквипатенциал беттер болады. Себебі: егер зарядтар цилиндр немесе шар

сфера тәрізді өткізгіштің осінде орналасса олардың электр өрісі күш сызықтары өткізгіштің бетіне радиалды бағытталған болады.

4. Өрістің күш сызықтары өріс нүктесіндегі потенциалдық жылдамырақ өзгеру бағытын көрсетеді. Сонымен біртекті өріс үшін эквипатенциал беттер

бір –бірімен бірдей қашықтықта орналасқан өрістің бағытына перпендикуляр сызықтар жүйесі болып табылады.

Кернеулік сызықтар эквипотенциалды беттерге үнемі нормаль бағытталады.

Өріс кернеулігі мен потенциалдың арасындағы байланысты белгілі өріс кернеулігі арқылы өрістің кез келген екі нүктесінің потенциалдар айырмасын анықтау үшін пайдалануға болады.

Кернеулік сызықтарыдеп әр нүктесінде жүргізілген жанамалары өрістің сол нүктесіндегі 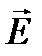кернеулік векторымен бағыттас болатындай етіп жүргізілген сызықтарды атайды. Кернеулік сызықтарын оларға перпендикуляр орналасқан бірлік бет арқылы өтетін сызықтар саны сол жердегі өріс кернеулігінің 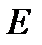модуліне тең (немесе пропорционал) болатындай қоюлықпен жүргізеді. Электростатикалық өрістің кернеулік сызықтары зарадтан басталып шексіздікке кетеді (оң заряд үшін), немесе, шексіздіктен келіп зарядта аяқталады (теріс заряд үшін).

Егер өрістің кез келген нүктесінде кернеулік векторының модулі және бағыты бірдей болса 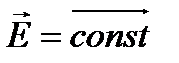, ондай өріс біртекті деп аталады. Біртекті өрістің кернеулік сызықтары біркелкі қоюлықпен жүргізілген өзара параллель сызықтар болып табылады.

Кернеулік векторының тұйқталған бет арқылы ағынын Гаусс теоремасы анықтайды:

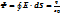
Кернеулік векторының ағыны деп –белгілі бір бетті тесіп өтетін кернеулік сызықтарының жалпы санына айтылады. Ағынды Ф - әріпімен белігілейміз.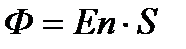

Егерде кернеулік бетке бұрыш астында түсетін болса онда cos 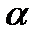қосылады.

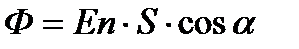. Ал егерде кернеулік бір текті болмаса онда кернеулік ағыны беттік интегралдау жолымен табылады.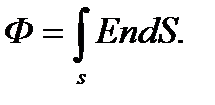

Егерде аудан мен кернеулік бір-біріне параллель болса онда кернеулік векторы нөлге айналады. Себебі: ф=0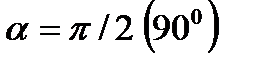

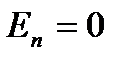
Бұдан мынадай тұжырым шығады. Егер кернеулік сызықтары нормальмен сүйір бұрыш жасаса 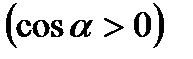онда кернеуліктің векторының ағыны үлкен нөл немесе оң болады. Ал 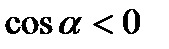болса онда вектордың ағыны кіші ноль немесе теріс таңбалы болады. Зарядтың сызықтық тығыздығы деп дененің бірлік ұзындығына келетін зарядты атайды:

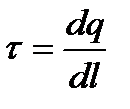, Кл/м.

Зарядтың беттік тығыздығыдеп аудан бірлігіне келетін зарядты атайды:

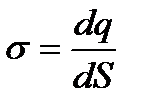, Кл/м².

Зарядтың көлемдік тығыздығыдеп дененің бірлік көлеміне келетін зарядты атайды:

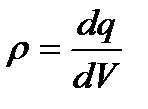, Кл/м³

Вакуумдегі электростатикалық өріс үшін Гаусс теоремасы: кез келген тұйық бет арқылы өтетін вакуумдегі электростатикалық өрістің кернеулік векторының ағыны сол бетпен қоршалған зарядтардың алгебралық қосындысының 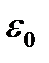-ге қатынасына тең:

.

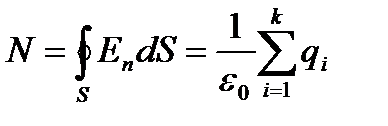1.Біртекті зарядталған шексіз жіптің өрісі

,

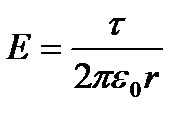мұндағы 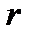- жіп пен қарастырылып отырған нүктенің ара қашықтығы.

2. Біртекті зарядталған шексіз жазықтықтың өрісі

.

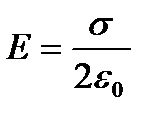3. Екі әр аттас зарядталған өзара параллель шексіз жазықтықтардың өрісі

.

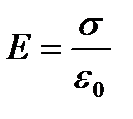4. Біртекті зарядталған сфералық беттің өрісі

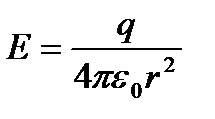
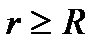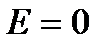
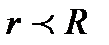үшін,

үшін,

мұндағы 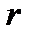- сфера центрінен өрістің қарастырылып отырған нүктесіне дейінгі ара қашықтық.

5. Көлем бойынша зарядталған шардың өрісі

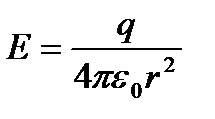
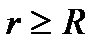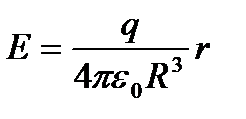
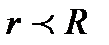үшін,

үшін,

мұндағы 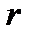- сфера центрінен өрістің қарастырылып отырған нүктесіне дейінгі арақашықтық.

Гаусс теоремасы симмериялы электр өрістерін есептеу үшін кең қолданылады. Бұл теореманы қолданып біркелкі зарядталған шексіз жазықтың, сфераның, цилиндрдің өрісн оп-оңай есептеп шығуға болады. Гаус теоремасының дифференциалдық түрі кеңістіктің белгілі бір нүктесіндегі өріс кернеулігін сол нүктедегі заряд тығыздығымен байланыстырады:

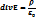
Электрлік ығысу векторы деп –сан жағынан электр кернеулік вектордың абсалюттік диэлектрлік өтімділік пен көбейтіндісіне тең шамаға айтылады. Ал абсалюттік диэлектриктік өтімділік деп вакумдағы диэлектрлік өтімділікпен ортадағы диэлектрлік өтімділіктің көбейтіндісіне айтылады. Оны Д әріпімен белгілейміз.

.

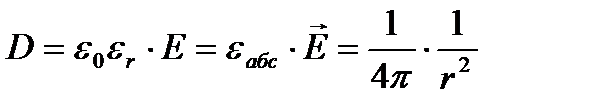
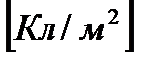Д – шама ортаның қасиетіне тәуелсіз.

Егер электрлік ығысу әртүрлі болса тағыда интегралдау жолымен табылады.

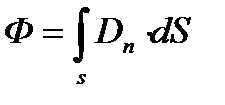
Электр диполі деп бірінен-бірі 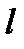ара қашықтыққа ығысқан екі шамалары бірдей 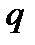және - 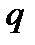әр аттас нүктелік зарядтан тұратын жүйені атайды. Егер 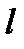ара қашықтығы жүйе өрісінің нүктелеріне дейінгі ара қашықтықпен салыстырғанда әлде-қайда кіші болса дипольді элементар дейді.

Теріс зарядтан оң зарядқа жүргізілген 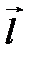векторы диполь иіні деп аталады.

Дипольдің электрлік моменті:

.

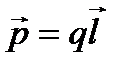Диполь өрісіоның электрлік моментімен анықталады:

,

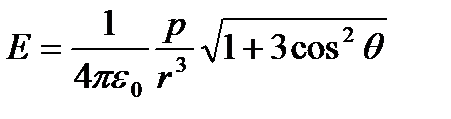мұндағы 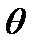– дипольдің 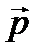моментінің бағыты мен дипольден өрістің қарастырылып отырған нүктесіне жүргізілген 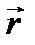радиус-векторының бағыты арасындағы бұрыш.

Сыртқы біртекті электр өрісінде дипольге қос күш әсер етеді. Қос күштің моментімына өрнекпен анықталады

.

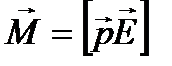Қос күш моментінің модулі мынаған тең

,

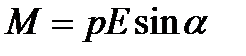мұндағы 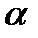– 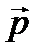векторы мен 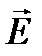өріс кернеулігінің арасындағы бұрыш.

Бұл қос күш 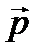және 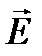векторлары бағыттас болатындай етіп дипольді бұруға тырысады. (7.1-сурет)

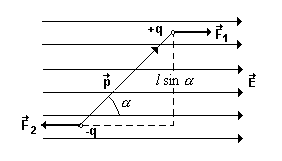7.1-сурет.

Егер диполь біртекті емес өрісте орналасып, өріске параллель жатпаса, онда дипольге оны өріске параллель болатындай етіп бұруға тырысатын қос күшпен бірге дипольді күштірек өріс аймағына тартатын күш әсер етеді.

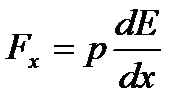
1. Екі әр аттас зарядталған өзара параллель шексіз жазықтықтың(жазық конденсатор) арасындағы потенциалдар айырмасы:

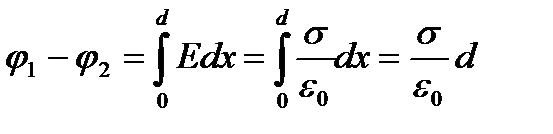, мұндағы 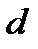- жазықтықтардың ара қашықтығы.

2. Екі зарядталған коаксиалды цилиндрдің (цилиндрлік конденсатор) арасындағы потенциалдар айырмасы: 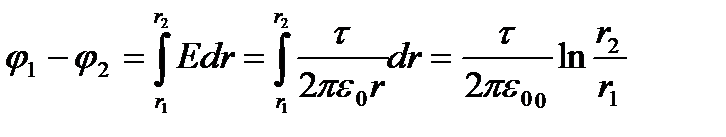, мұндағы 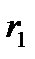және 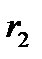– цилиндлердің радиустары.

3. Екі зарядталған концентрлі сфераның арасындағы (сфералық конденсатор) потенциалдар айырмасы:

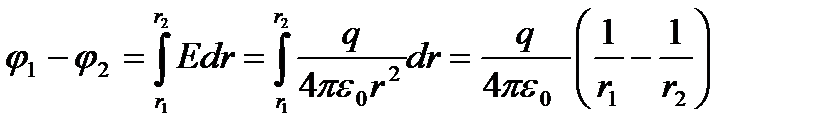
Оқшауланған өткізгіштің потенциалы оның зарядына пропорционал:

.

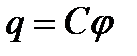Потенциал мен заряд арасындағы 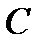пропорционалдық коэффициенттін өткізгіштің электр сыйымдылығы деп атайды. Сыйымдылық сан жағынан өткізгіштің потенциалын бір өлшемге арттыру үшін өткізгішке берілетін зарядқа тең:

.

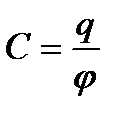Электр сыйымдылығының өлшем бірлігі - фарад (Ф): 1Кл заряд берілгенде потенциалын 1 В-қа өзгертетін оқшауланған өткізгіштің сыйымдылығы 1Ф-қа тең деп алынады.

Өткізгіштің сыйымдылығы оның өлшемдері мен пішініне тәуелді. Мысалы, радиусы 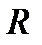шар тәрізді өткізгіштің сыйымдылығы: .

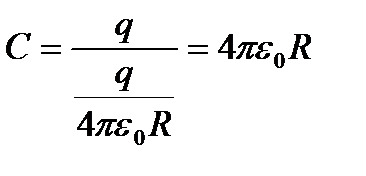Өлшемдері шамалы және қоршаған денелермен салыстырғанда потенциалы азғантай болғанымен, өздерінде едәуір зарядты жинақтай алатын құрылғыны конденсатор деп атайды. Конденсатор бірінен-бірі диэлектрик қабатымен бөлінген қос өткізгіштен (астарлардан) тұрады. Өріс конденсатордың ішінде ғана жинақталады, ал кернеулік сызықтары оның бір астарларынан басталып екіншісінде аяқталады.

Конденсатордың сыйымдылығынмына өрнектің көмегімен анықтайды:

,

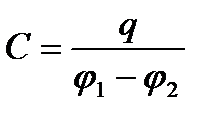мұндағы – астарлардың біреуіндегі заряд, 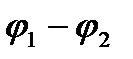- конденсатор астарларының арасындағы потенциалдар айырмасы.

Вакуумді конденсатордың сыйымдылығы 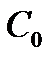, ал астарлары арасындағы кеңістік біртекті диэлектрикпен толтырылған сол конденсатордың сыйымдылығы 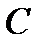болсын. Сонда

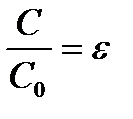
қатынасын диэлектриктің салыстырмалы диэлектрлік өтімділігі деп атайды.

1. Жазық конденсатордың сыйымдылығы

,

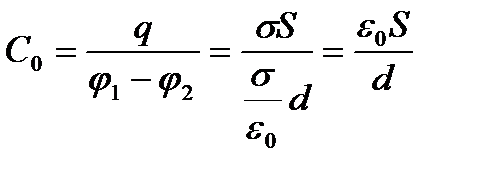ал диэлектрикпен толтырылған жазық конденсатордың сыйымдылығы

.

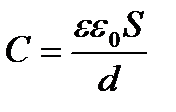2. Цилиндрлік конденсатордың сыйымдылығы

,

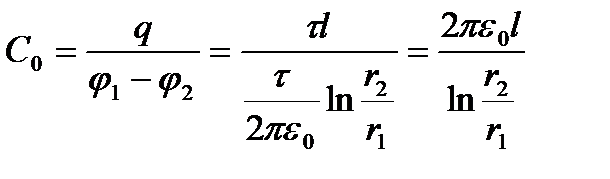ал диэлектрикпен толтырылған цилиндрлік конденсатордың сыйымдылығы

.

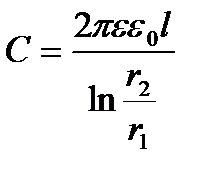3. Сфералық конденсатордың сыйымдылығы

,

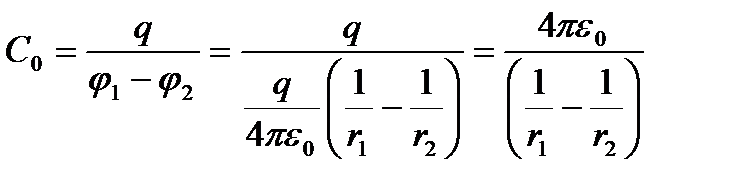ал диэлектрикпен толтырылған сфералық конденсатордың сыйымдылығы

.

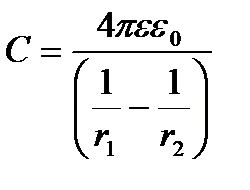Берілген кернеу үшін керекті сыйымдылықты алу мақсатында конденсаторларды бір-бірімен батарея құрып жалғайды.

1. Конденсаторларды параллель жалғау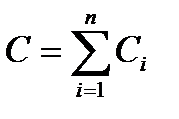

2. Конденсаторларды тізбектей жалғау .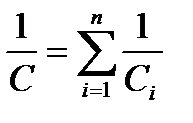

Өткізгіштің ішкі бөліктерінде зарядтың болмауы Гаусс теоремасының салдары болып табылады. Ал Гаусс теоремасының өзі Кулон заңына негізделген.

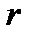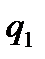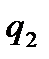Бір бірінен ара қашықтықта орналасқан нүктелік және зарядтардың өзара потенциалдық энергиясын 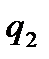зарядының өрісінде орналасқан 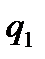зарядының потенциалдық энергиясы, немесе 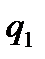зарядының өрісінде орналасқан 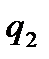зарядының потенциалдық энергиясы деп қарастыруға болады:

,

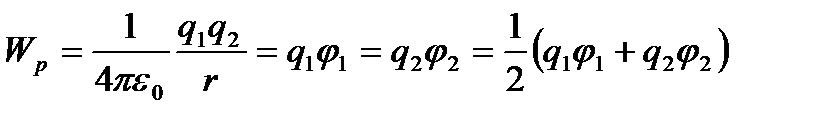мұндағы 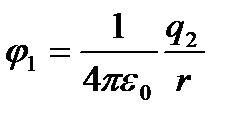және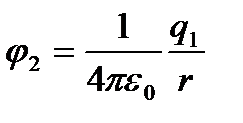

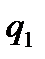- заряды орналасқан нүктедегі 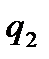заряды тудыратын және 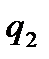заряды орналасқан нүктедегі 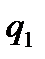заряды тудыратын потенциалдарға сәйкес.

Тыныштық күйдегі 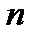заряд үшін нүктелік зарядтар жүйесінің өзара әрекеттесу энергиясы

,

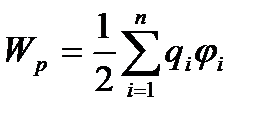мұндағы 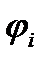– жүйенің 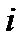-ші зарядынан басқа, барлық зарядтарының 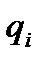заряды орналасқан нүктедегі тудыратын потенциалы:

.

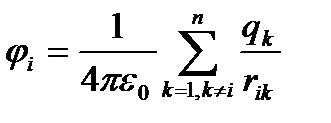Оқшауланған өткізгіштің беті эквипотенциалды болып табылады, яғни 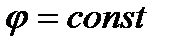. Өткізгіш бетіндегі зарядты 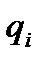нүктелік зарядтар жүйесі деп қарастыруға болады. Сонда

.

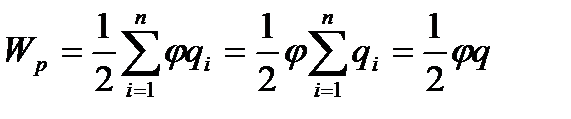Өткізгіш бетіндегі зарядпен оның потенциалының арасындағы байланысты ескере отырып, зарядталған өткізгіштің энергиясы үшін төмендегідей өрнектерді жазуға болады:

.

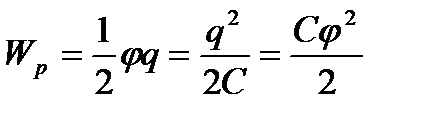Заряды + конденсатор астарының потенциалы 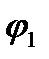-ге, ал заряды - астарының потенциалы 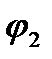–ге тең болды делік. Сонда

.

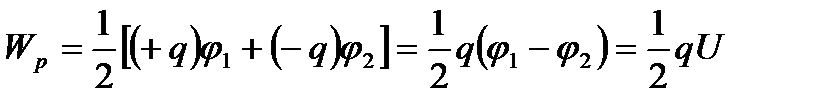Конденсатор астарларындағы заряд пен олардың арасындағы потенциал айырмасының байланысын ескере отыра зарядталған конденсатор энергиясы үшін мына өрнектерді жазуға болады:

.

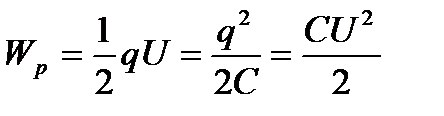Конденсатор астарлары бір-бірін тартатын механикалық (пондеромоторлық) күшті жазық конденсатордың потенциалдық энергиясы арқылы анықтауға болады:

.

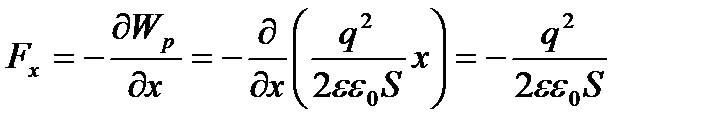Зарядталған конденсатордың энергиясы оның электр өрісінде, яғни оның астарларының арасындағы кеңістікте шоғырланған. Конденсатордың энергиясын оның электр өрісін сипаттайтын шамалар арқылы өрнектеуге болады. Жазық конденсатор үшін мына өрнекті жазуға болады:

,

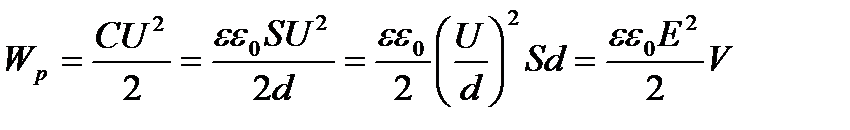мұндағы 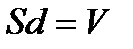- өрістің алып отырған көлемі.

Егер өріс біртекті болса, онда оның ішіндегі энергия кеңістікте 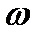тұрақты тығыздықпен таралады:

.

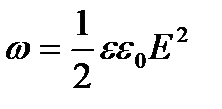Электр тогы деп зарядтардың реттелген қозғалысын айтамыз. Электр тогын сандық сипаттау үшін ток күші деген шама енгізіледі. Ток күші деп өткізгіштің көлденең қимасынан бірлік уақытта өтетін зарядты айтады:

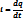
Тұрақты тогт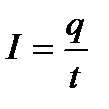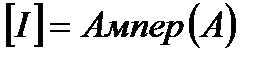а 1А=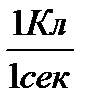

Электр тогының пайда болудың екі шарты бар:

1. зарядтар денеде атомдармен байланысты болмаған еркін электрондар.

2. Сол электрондарды бағытталған, қозғалысқа келтіретін электр өрісі болуы керек.

Ом өткізгіш ұштарындағы кернеу мен онан өтетін ток күшін байланыстыратын заңдылықты ашты:

I=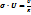

Металдарда пайда болған ток кернеуге пропорционал.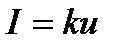

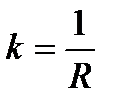
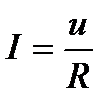Тізбек бөлігі үшін Ом заңы.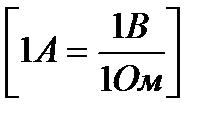

Тұрақты ток – деп уақыт өтуімен шамасы және бағыты өзгермес болатын токтарға айтылады. Тұрақты токты акуммулятор, голвани элементтер, батарейкалар береді және олар тұрақты ток көздері болып саналады.

Электростатикалық күштердің тұйық контурдағы жұмысы нөлге тең, сондықтан тұрақты ток жүру үшін тізбекте табиғаты кулондық емес күштер керек. Бұл күштерді тосын (бөгде) күштер деп атайды. Тосын күштердің бірлік зарядқа әсер ететін күшін Э.қ.к. (электр қозғаушы күш–ε) деп атайды. Егер тізбек бөлігінде тосын күштер әсер етсе Ом заңын (тізбектің бір текті емес бөлігі үшін) былай жазуға болады:

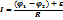
Электр қозғаушы күш –деп еркін зарядтарды тасымалдау жұмысын жасайтын бөгде күштерге айтылады. Оны ток көздері тудырады. Оны

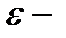эпсилион мен белгілейміз.

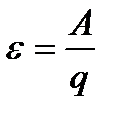
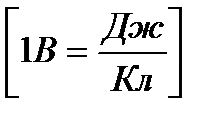
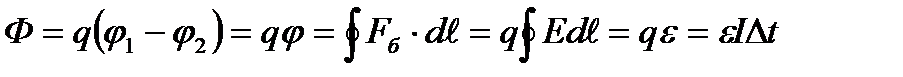
Егер тізбек тұйықталған болса Ом заңын төмендегіше жазуға болады:

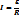
Ток жүріп тұрған өткізгіш ішіндегі өріс кернеулігі мен ток тығыздығын байланыстыратын теңдеді Ом заңының дифференциалды түрі деп атайды:

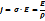
Ток тығыздығы деп -тізбектегі тогтың өткізгіш көлденең қимасынан өтіп тұратын зарядтан концентрациясымен жылдамдығының көбейтіндісіне айтылады. Немесе жай тілмен айтқанда өтіп жатқан ток күшінің сол жердегі көлденең қимасын айтады.

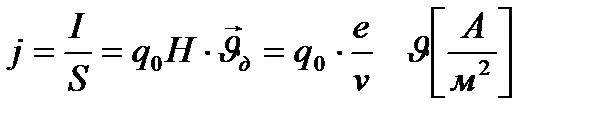
Өткізгіштегі электр күш теоремасы – дегенде өткізгіш арқылы электрондардың қозғалысымен түсіндіретін теорияға айтылады. Мұны бірінші болып экспериментте 1913 ж совет физиктері Монделштам және Пополекси 1916 ж Америка физиктері өз тәжірибелерінде дұрыс екендігі

дәлелдеген.

Осы теорема бойынша жүзеге келетін электр өрісі.

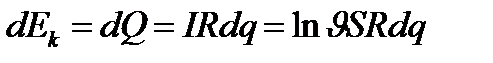мұны Джоуль – Ленц тапқан.

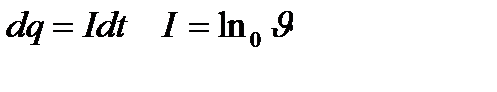
n – консентрация – көлем бірлігіндегі молекулалар саны.

Катушкаға оралған сымның көлемі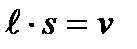

Егерде көлем бойынша қозғалыс мөлшерін өзгерісі мен өрісінің өзгерісін өзара тең деп алып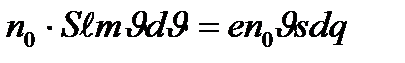

Өзара тең деп алсақ онда dq –ды табамыз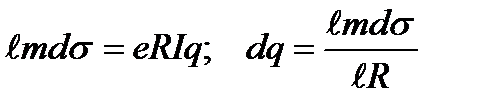

Тармақталған тізбектер. Кирхгоф ережелері. Тұрақты токтың жұмысы мен қуаты. Джоуль–Ленц заңы және оның дифференциалды түрі.

Тармақталған тізбектерді есептеу үшін Кирхгоф тағайындаған екі ережені қолданады: бірінші ереже, түйіндегі токтардың алгебралық қосындысы нөлге тең; екінші ереже, контурдағы кернеу құлауларының алгебралық қосындысы сол контурдағы э.қ.к. қосындысына тең

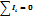
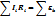
Тұрақты токтың жұмысы мен қуатын энергияның сақталу заңын қолданып алады. Джоуль мен Ленц тәжірбе жүзінде ток жүріп тұрған өткізгіштен бөлінетін жылуды есптеп шығаратын заңдылықты тапты:

Q = I²Rt = IUt

Токтың жұмысы деп - тогы бар тізбектен уақыт бойынша өтіп тұрған тог күші өткізгіш ұштарындағы кернеу және осы уақыттың шамаларының көбейтіндісіне тең болған физикалық шамаға айтылады.

Тізбектеп қосылса А=I²Rt A=IUt, параллель қосылса

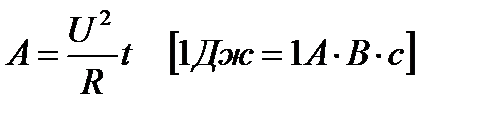
Джоуль- Ленц заңы тогы бар өткізгіштен ажыралып шығатын жылулық мөлшері сондағы токтың атқарған жұмысына тең болады.

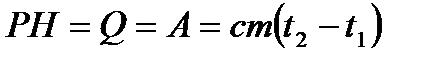бұл табиғаттағы заттардың орын ауыстыруынан болатын жұмыс 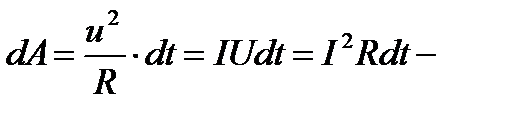бұл дегеніміз тұрақты токтың атқарған жұмысы сол токтың өту уақыты мен анықталады.Өйткені бұл жерде

t- өзгеріп тұрады.

Ом заңы 1 заңы тізбектің бір бөлігі үшін Ом заңы деп өткізгіштен өтіп жатқан ток күші оған қиылған кернеу тура пропорцианал, ал кедергіге кері пропорционал болады.

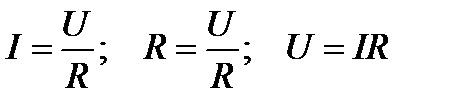
2- заңы. Толық тізбек үшін Ом заңы деп – тізбектен өтіп жатқан ток күші оған қосылған электр қозғаушы күшіне тура тізбек кедергісімен ток көзі ішкі кедергісінің қосындысына кері пропорционал болады.

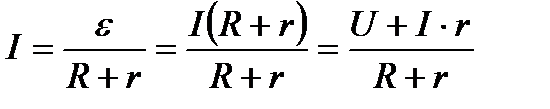
3. Электр кедергісі металдар үшін.

Металдық меншікті кедергісі мен ұзындығының көбейтіндісіне тура пропорционал ал көлденең қимасының ауданына кері пропорционал болады.

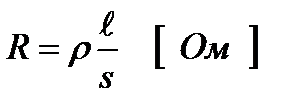
4. Заттың ішкі кедергісі.

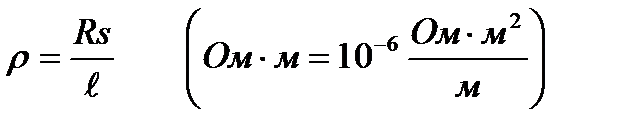
Көлденең қимасының ауданы 1 мм²-да берілсе онда 10^-6 жүреді.

5. Электр өткізгіштік -деп заттың электр кедергісіне кері болған физикалық шамаға айтылады. Өлшем бірлігі: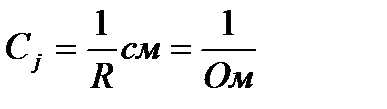

6. Өткізгіштің Вольт Амперлік сипаттамасы –деп әр түрлі өткізгіштердегі токтың кернеуге байланысқан тәуелділігін айтады.

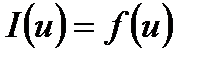
7. Меншікті электр өткізгіштік – деп өткізгіштің меншікті кедергісіне кері болған физикалық шамаға айтылады. Оны j- мен белгілейміз.

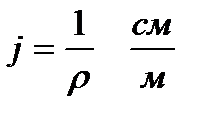
8. Ом заңының дифференциалдық түрі.