Индексы переменного состава, постоянного состава и структурных сдвигов
Задача оценки влияния изменения индивидуальных значений осредняемого показателя и структуры явления на общую динамику средней величины решается с помощью построения системы взаимосвязанных индексов: переменного состава, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних с изменяющимися (переменными) весами, показывающее изменение индексируемой средней величины. Для любых качественных показателей индекс переменного состава можно записать в общем виде:

где  – уровни осредняемого показателя в отчётном и базисном периодах соответственно;
– уровни осредняемого показателя в отчётном и базисном периодах соответственно;
 – веса (частоты) осредняемого показателя в отчётном и базисном периодах соответственно.
– веса (частоты) осредняемого показателя в отчётном и базисном периодах соответственно.
Индекс, характеризующий динамику средней величины при одной и той же фиксированной структуре совокупности, называется индексом постоянного (фиксированного) состава и исчисляется по формуле
 .
.
После сокращения на  формула примет вид агрегатного индекса качественного показателя:
формула примет вид агрегатного индекса качественного показателя:

Индекс постоянного состава показывает, как в отчётном периоде по сравнению с базисным изменилось среднее значение показателя по какой-либо однородной совокупности за счёт изменения только индивидуальных значений индексируемой величины, т.е. когда влияние структурных сдвигов устранено.
Для оценки влияния только структурных изменений на исследуемый средний показатель исчисляют индекс структурных сдвигов как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчётную структуру, к средней величине этого показателя в базисном периоде:

В качестве весов (частот) индексов средних величин наряду с абсолютными показателями f могут использоваться и относительные показатели (доли, частости) d.
Так как  ,
, 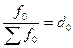 , то приведённые выше формулы будут иметь вид:
, то приведённые выше формулы будут иметь вид:
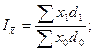


где  – доли единиц с определённым значением признака в общей совокупности в отчётном и базисном периодах соответственно, при этом
– доли единиц с определённым значением признака в общей совокупности в отчётном и базисном периодах соответственно, при этом  .
.
Между индексами существует взаимосвязь:
 .
.
Территориальные индексы
При характеристике территориальной вариации цен по предприятиям, городам, районам и пр.) по совокупности товаров используется территориальные индексы.
При двухсторонних сравнениях территориальный индекс рассчитывается по формуле


где PiA и РiБ – цена i-го товара в регионе А и Б соответственно;
Qi = QiA + QiБ – общий по двум регионам объём продаж i-го товара.
Индекс показывает, насколько цены на товары в регионе А отличаются от цен в регионе Б.
В формуле данного территориального индекса можно использовать стандартизованные веса – объёмы продажи данных видов продукции по более крупному территориальному образованию, например, по республике. В этом случае индекс имеет вид:

где Qi респ. – объём продажи i-го товара по республике в целом.
Для того чтобы определить, насколько цены на товары в данном регионе отличаются от средних по более крупному территориальному образованию, например, по республике, территориальный индекс цен может быть приведён к следующему виду:
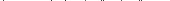 |
где  – средняя по республике цена i-го товара.
– средняя по республике цена i-го товара.
 |
Второй способ расчёта территориальных индексов цен учитывает соотношение весов сравниваемых территорией. При этом вначале следует определить среднюю по двум территориям цену каждого товара (
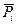 ):
): где pi – цена i-го товара в каждом регионе;
qi – объём продажи i-го товара в каждом регионе.
После этого рассчитывается территориальный индекс цен:
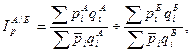
где qiА и qiБ – объём продажи i-го товара в регионе А и Б соответственно.
Решение типовых задач
Пример 5.1
Имеются следующие данные по предприятию о реализации продукции:
| Вид продукции | Продано, тыс.шт. | Отпускная цена за шт., руб. | ||
| I квартал, q0 | II квартал, q1 | I квартал, p0 | II квартал, p1 | |
| А | 2 500 | 2 610 | 44,8 | 45,4 |
| Б | 3 000 | 2 950 | 47,1 | 47,6 |
| В | 3 600 | 3 700 | 55,0 | 55,7 |
Определим:
1) изменение (в %) объёма реализации каждого вида продукции, а также изменение объёма реализации продукции в целом по предприятию;
2) изменение цен (в %) по каждому виду продукции и среднее изменение цен по всему ассортименту продукции;
3) абсолютное изменение общей стоимости реализованной продукции, выделив из общей суммы изменение за счёт изменения количества продукции и за счёт изменения цен.
Решение
1. Для характеристики изменения объёма реализации каждого вида продукции исчисляются индивидуальные индексы физического объёма:
 .
.
Продукция А:  , или 104,4%, т.е объём реализации увеличился на 4, 4% (104,4-100).
, или 104,4%, т.е объём реализации увеличился на 4, 4% (104,4-100).
Продукция Б: 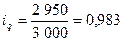 , или 98,3%, следовательно, объём реализации снизился на 1, 7 % (98,3 – 100).
, или 98,3%, следовательно, объём реализации снизился на 1, 7 % (98,3 – 100).
Продукция В:  или 102,8%, т.е объём реализации вырос на 2,8 % (102,8 – 100).
или 102,8%, т.е объём реализации вырос на 2,8 % (102,8 – 100).
Для характеристики изменения объёма реализации в целом по предприятию исчисляется общий индекс физического объёма:
 или 101,8 %.
или 101,8 %.
Следовательно, в целом по предприятию объём реализации продукции увеличился на 1,8 %, в результате стоимость продукции увеличилась на 8 073 тыс. руб. (459 373 – 451 300).
2. Для характеристики изменения цен по каждому виду продукции используются индивидуальные индексы цен:
 .
.
Продукция А:  , или 101,3%, следовательно, цена повысилась на 1,3 % (101,3 – 100).
, или 101,3%, следовательно, цена повысилась на 1,3 % (101,3 – 100).
Продукция Б:  или 101,1%, т.е цена возросла на 1, 1%, (101,1 – 100).
или 101,1%, т.е цена возросла на 1, 1%, (101,1 – 100).
Продукция В:  или 101,3%, т.е имеет место увеличение цены на 1,3 % (101,3 – 100) .
или 101,3%, т.е имеет место увеличение цены на 1,3 % (101,3 – 100) .
Среднее изменение цен по всему ассортименту продукции определяется по формуле общего индекса цен:
 или 101, 2%.
или 101, 2%.
Таким образом, цены на продукцию предприятия увеличились в среднем на 1,2 %, за счёт чего стоимость продукции выросла на 5 631 тыс. руб. (465 004 – 459 373).
3. Абсолютное изменение общей стоимости реализованной продукции определяется по формуле
 тыс. руб.,
тыс. руб.,
Абсолютное изменение стоимости продукции за счёт изменения выпуска продукции:  =8 073 тыс. руб. (см. решение п.1);
=8 073 тыс. руб. (см. решение п.1);
Абсолютное изменение стоимости продукции за счёт изменения цен:  =5 631 тыс. руб. (см. решение п.2).
=5 631 тыс. руб. (см. решение п.2).
Абсолютное изменение общей стоимости реализованной продукции равно алгебраической сумме изменения стоимости за счёт количественного и качественного факторов:
 тыс. руб.
тыс. руб.
Пример 5.2
Имеются следующие данные о продаже товаров в универмаге города:
| Товарная группа | Продано в предыдущем периоде, тыс. руб. | Изменение количества проданных товаров в отчётном периоде по сравнению с предыдущим, % |
| Видеотехника | +15 | |
| Бытовая техника | +12 |
Определим индекс физического объёма товарооборота.
Решение
Для определения изменения физического объёма продаж в целом по универмагу используется формула среднего взвешенного арифметического индекса:

где 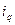 – индивидуальные индексы физического объёма, индивидуальные индексы физического объёма.
– индивидуальные индексы физического объёма, индивидуальные индексы физического объёма.
Так как известно изменение количества продажи каждого вида продукции, то индивидуальные индексы физического объёма составят:
видеотехника 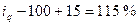 , или 1,15;
, или 1,15;
бытовая техника  , или 1,12.
, или 1,12.
Общий индекс физического объёма товарооборота:
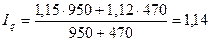 , или 114%, т.е. рост составил 14%.
, или 114%, т.е. рост составил 14%.
Следовательно, физический объём продаж в текущем периоде по сравнению с базисным увеличился на 14%.
Пример 5.3
Имеются следующие данные о реализации мебели:
| Вид продукции | Товарооборот в действующих ценах, тыс. руб. | Изменение средних цен в июне по сравнению с маем, % | |
| май | июнь | ||
| Диваны | + 14 | ||
| Кресла | – 4 | ||
| Столы | + 12 |
Определим изменение цен на проданную мебель, общий индекс товарооборота и физического объёма продаж.
Решение
1. Общий индекс цен определим, используя формулу для расчёта среднего взвешенного гармонического индекса:
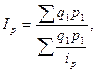
где  – индивидуальные индексы цен.
– индивидуальные индексы цен.
Индивидуальные индексы цен:
диваны – 100 + 14 = 114%, или 1,14;
кресла – 100 - 4 = 96%, или 0,96;
столы – 100 + 12 = 112%, или 1,12.
Общий индекс цен:
 или 106, 4%.
или 106, 4%.
Следовательно, цены на проданную мебель в среднем увеличились на 6,4%. Сумма дополнительных расходов потребителей, вызванных ростом цен, составила 13,658 тыс. руб. (226 – 212, 342).
2. Общий индекс товарооборота:
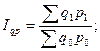
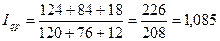 , или 108,5 %.
, или 108,5 %.
Таким образом товарооборот в июне по сравнению с маем вырос на 8,5%, что в денежном выражении составило 18 тыс. руб. (226 – 208).
3. Общий индекс физического объёма продаж:

 или 102 %.
или 102 %.
Количество проданных товаров выросло на 2% или на 4 342 тыс. руб. (212,342 – 208).
Между вычисленными индексами существует взаимосвязь:
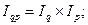 1,085=1,064×1,02=1,085;
1,085=1,064×1,02=1,085;
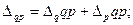 18=13,658+4,342.
18=13,658+4,342.
Таким образом товарооборот в июне по сравнению с маем вырос на 8,5 %, или на 18 тыс. руб., в том числе за счёт повышения цен – на 6, 4%, или на 13, 658 тыс. руб., за счёт увеличения физического объёма продаж – на 2 %, или на 4 342 тыс. руб.
Пример 5.4
Имеются следующие данные о реализации одного вида продукции по группе торговых предприятий:
| Предприятие | Реализовано продукции, тыс. руб. | Цена единицы продукции, руб. | |||||||
| IV квартал прошедшего года | IV квартал текущего года | IV квартал прошедшего года | IV квартал текущего года | ||||||
| тыс. шт | в % от общего объёма | тыс. шт | в % от общего объёма | ||||||
| Магазин №1 | 106,2 | 113,1 | |||||||
| Магазин №2 | 179,1 | 187,1 | |||||||
| Магазин №3 | 256,5 | 276,0 | |||||||
Определим в целом по группе предприятий: 1) изменение средней цены единицы продукции в процентах и абсолютном размере; 2) изменение средней цены по группе предприятий в результате изменения цены на отдельных предприятиях и за счёт структурных сдвигов в общем объёме реализованной продукции.
Решение
Для характеристики динамики средней цены рассчитаем индексы переменного состава, постоянного состава и структурных сдвигов. Результаты расчётов представлены в таблице:
| Относительные изменения | Абсолютные изменения |
| Индекс переменного состава | |
 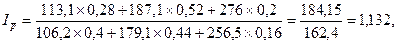 или 113, 2%, т.е прирост составил 13, 2% или 113, 2%, т.е прирост составил 13, 2% |  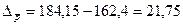 руб. руб. |
| Индекс фиксированного состава | |
 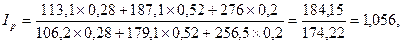 или 105,6 %, т.е прирост составил 5.6 % или 105,6 %, т.е прирост составил 5.6 % | 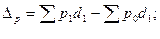 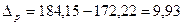 руб. руб. |
| Индекс структурных сдвигов | |
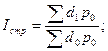  или 107, 2 %, т.е прирост составил 7, 2% или 107, 2 %, т.е прирост составил 7, 2% |   руб. руб. |
| Проверка | |
 1,132 = 1,056×1,072 1,132 = 1,056×1,072 |  21,75=9,93+11,82 21,75=9,93+11,82 |
Таким образом в отчётном периоде (IV кв. текущего года) по сравнению с базисным (IV кв. предыдущего года) средний уровень цены продукции по группе торговых предприятий увеличился на 13,2% (21,75 руб.); в том числе в результате изменения цены продукции на каждом предприятии – на 5,6% (9,93 руб.); в результате роста удельного веса предприятий с более высокой ценой и произошедших структурных сдвигов – на 7,2% (11,82 руб.);
3) в результате совместного действия вышеназванных факторов средний уровень цены продукции.
Следовательно, произошедшие в структуре совокупности изменения оказали более существенное влияние на изменение среднего уровня цены продукции по совокупности в целом, чем рост цен на отдельных предприятиях.
Пример 5.5
Известны цены и объёмы реализации товаров по двум регионам:
| Товар | Регион А | Регион Б | ||
| цена, руб. РА | объём реализации, т qA | цена, руб. PA | объём реализации, т qБ | |
| 21,0 18,4 27,2 | 23,0 20,7 25,8 |
Рассчитаем территориальный индекс цен двумя способами.
Способ 1
Территориальный индекс цен составит
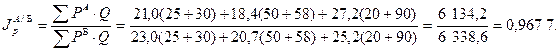
Следовательно, цены в регионе А на 3,23 % ниже цен в регионе Б.
Этому выводу не противоречит и обратный индекс:
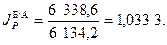
Способ 2
Территориальный индекс цен определяется по формуле

Рассчитаем среднюю по двум территориям цену каждого товара

Средняя цена составит

Территориальный индекс цен составит:

