Функция Лагранжа простейших систем

Рассмотрим системы с одной степенью свободы.

1. Плоский математический маятник (Рис.3).

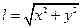- уравнение связи.

Число степеней свободы равно единице (см. §1).

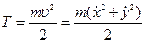- кинетическая энергия.

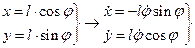
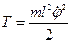
U – потенциальная энергия.

U=mgh, где h – уровень подъёма над положением равновесия.

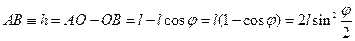
Имеем :

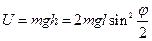
Рассмотрим случай малых колебаний:

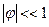, φ – измеряется в радианах.

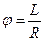
L – длина дуги, R – радиус окружности. Тогда:

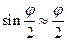
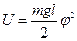
Функция Лагранжа:

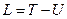
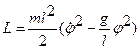
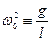
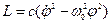
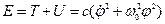
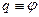
Уравнение движения:

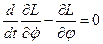
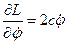
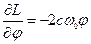
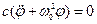
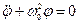
Для решения дифференциального уравнения второго порядка необходимо два начальных условия:

1)

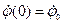
2)

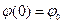
2. Линейный гармонический осциллятор (Рис.4).

k – упругость пружины,

l₀ – длина пружины в недеформированном состоянии,

l – длина пружины в деформированном состоянии.

По закону Гука (для малых деформаций):

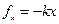
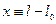
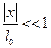- малые деформации.

По второму закону Ньютона:

,

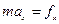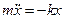
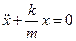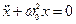, , где .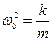

Решение аналогично случаю 1. Начальные условия:

1)

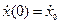
2)

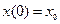
3. Аналогично для вертикального гармонического осциллятора (Рис.5)

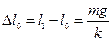(По закону Гука)

В данном случае: 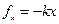- не является результирующей силой, а лишь возвращающей систему к положению равновесия.

Задачи

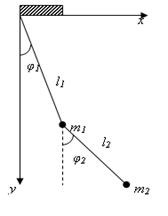1.Наити функцию Лагранжа двойного плоского маятника , находящегося в однородном поле тяжести (ускорение силы тяжести g).

Решение. в качестве координат берём углы φ₁ и φ₂, которые нити l₁ и l₂ образуют с вертикалью. Тогда для точки m₁ имеем:

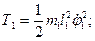
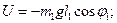
чтобы найти кинетическую энергию второй точки, выражаем её декартовы координаты x₂, y₂ (начало координат в точке подвеса, ось y – по вертикали вниз) через углы φ₁ и φ₂:

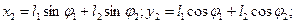
после этого получим:

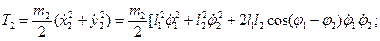
окончательно:

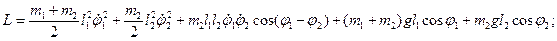
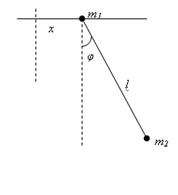2.Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m₂, точка которого (с массой m₁ в ней) может совершать движения по горизонтальной прямой.

Решение. Вводя координату x точки m₁ и угол φ между нитью маятника и вертикалью, получим:

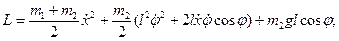
Интегралы движения в методе Лагранжа.

Динамические переменные в методе Лагранжа – это обобщённые координаты и обобщённые скорости. Всего их 2n, они задают начальное состояние систем.

Интеграл движения – это функция динамических переменных и времени 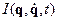, сохраняющая своё значение при движении системы (в КП).

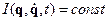- постоянство означает, что полная производная по времени должна быть равна нулю:

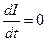
При n=1 имеем:

, .

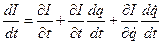
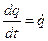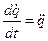Преобразование Галилея.

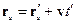
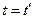
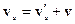
Преобразование импульса:

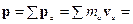
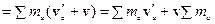
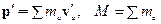
Тогда:

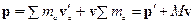
Рассмотрим такую систему отсчёта 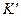, в которой полный импульс системы 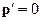(это есть система центра масс), тогда имеем:

,

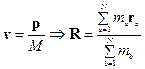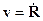
где 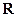- радиус вектор центра масс