Статический приемочный контроль качества продукции
Под статическим приемочным контролем качества продукции понимают выборочный контроль, основанный на применении методов математической статистики для проверки соответствия качества продукции установленным требованиям. Основная идея такого контроля состоит в том, что о качестве контролируемой партии продукции судят по выборочным характеристикам, определяемым по малой выработке из этой партии.
Термины относящиеся к статистическому приемочному контролю качества продукции, регламентированы ГОСТ 15895-77 «Статистические методы управления качеством продукции. Термины и определения»
Контролируемая партия продукции (далее партия) – «предназначенная для контроля совокупность единиц продукции одного наименования, типономинала или типоразмера и исполнения, произведенная в течение определенного интервала времени в одних и тех же условиях».
Объем партии – «число единиц продукции, составляющих партию».
Выборочный контроль – «контроль, при котором решение о качестве контролируемой продукции принимается по результатам проверки одной или нескольких выборок или проб из партии или потока продукции».
Выборка – «изделие или определенная совокупность изделий выбранных для контроля из партии или потока продукции».
Объем выборки – «число изделий, составляющих выборку».
Различают контроль по количественному и качественному признаку.
Контроль по количественному признаку – «контроль качества продукции в ходе которого определяют значения одного или нескольких ее параметров, а последующее решение о контролируемой совокупности принимают в зависимости от этих значений».
Контроль по качественному признаку – «контроль качества продукции, в ходе которого каждую проверенную ее единицу относят к определенной группе, а последующее решение о контролируемой совокупности принимают в зависимости от соотношения чисел».
Статистический приемочный контроль качества продукции является контролем по альтернативному признаку – «контролем по качественному признаку, в ходе которого каждую проверенную единицу продукции относят к категории годных или дефектных, а последующее решение о контролируемой совокупности принимают в зависимости от числа обнаруженных в выборке или пробе дефектных единиц продукции или числа дефектов, приходящегося на определенное число единиц продукции» (ГОСТ 15895-77).
Результат выборочных испытаний случаен. Это означает, что при сколь угодно высоком значении истинной надежности контролируемой партии, всегда существует отличная от нуля вероятность забракования годной продукции, и наоборот, партия, обладающая низкой надежностью, может быть принята.
Данные для планирования контрольных испытаний задают в виде двух уровней дефектности: приемочного и браковочного.
Уровень дефектности – «доля дефектных единиц продукции или число дефектов на сто единиц продукции» (ГОСТ 15895-77).
Доля дефектных единиц продукции  определяется отношением числа дефектных единиц продукции
определяется отношением числа дефектных единиц продукции  к общему числу единиц продукции в партии
к общему числу единиц продукции в партии 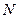 :
:
 .
.
В математическом плане задача выборочного контроля относится к статической проверке гипотез. В статистике различают два вида гипотез: простые и сложные.
Простой гипотезой – называется такое предположение относительно величины параметра  , которое определяет единственное значение этого параметра. Например, гипотеза будет простой. если предположить, что
, которое определяет единственное значение этого параметра. Например, гипотеза будет простой. если предположить, что  .
.
Сложной гипотезой – называется предположение относительно величины параметра  , согласно которому параметр может принимать больше одного значения. Предположение, что
, согласно которому параметр может принимать больше одного значения. Предположение, что  будет представлять сложную гипотезу.
будет представлять сложную гипотезу.
В задаче выборочного контроля выдвигается 2 простые гипотезы:
 - качество партии соответствует приемочному уровню дефектности
- качество партии соответствует приемочному уровню дефектности  ;
;
 - качество партии соответствует браковочному уровню дефектности
- качество партии соответствует браковочному уровню дефектности  .
.
При различении двух простых гипотез возможны ошибки двух родов:
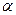 - ошибка первого рода – вероятность принятия гипотезы
- ошибка первого рода – вероятность принятия гипотезы  , когда на самом деле имеет место гипотеза
, когда на самом деле имеет место гипотеза  ;
;
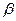 - ошибка второго рода – вероятность принятия гипотезы
- ошибка второго рода – вероятность принятия гипотезы  , когда на самом деле имеет место гипотеза
, когда на самом деле имеет место гипотеза  .
.
В теории надежности вероятность 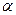 называется риском поставщика, а
называется риском поставщика, а 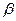 - риском потребителя.
- риском потребителя.
Риск поставщика – «вероятность забракования партии продукции, обладающей приемочным уровнем дефектности» (ГОСТ-15895-77).
Риск потребителя – «вероятность приемки партии продукции, обладающей браковочным уровнем дефектности» (ГОСТ-15895-77).
Одна из важнейших характеристик контрольных испытаний – оперативная характеристика, показывающая, насколько хорошо данное решающее правило отвечает своему назначению – принятию правильного решения.
Оперативная характеристика плана статистического приемочного контроля – «выраженная уравнением, графиком или таблицей и обусловленная определенным планом контроля зависимости вероятности приемки партии от величины, характеризующей качество этой продукции (ГОСТ 15895-77).
Типичный вид оперативной характеристики показан на рис. 6 сплошной линией.
Легко представить себе идеальный план контроля (оперативная характеристика, показанная рис.6 пунктирной линией «а»), при котором партии с фактическим уровнем качества выше некоторого критического значения (  ) с вероятностью 1 принимались бы, а не отвечающие требованиям – безусловно браковались. При этом риск и поставщика, и потребителя был бы равен нулю.
) с вероятностью 1 принимались бы, а не отвечающие требованиям – безусловно браковались. При этом риск и поставщика, и потребителя был бы равен нулю.
В общем случае оперативная характеристика – монотонно невозрастающая функция. Чем ближе она к идеальной, тем большее число наблюдений (в среднем) требуется для принятия решения.
Наибольшее распространение на практике подучили три вида приемочного контроля:
— одноступенчатый — решение о принятии или забраковании партии продукции принимают по результатам контроля только одной выборки или пробы;
— многоступенчатый — решение о принятии или забраковании партии принимается на основании последовательных испытаний 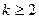 выборок или проб, причем максимальное их количество заранее установлено (обычно
выборок или проб, причем максимальное их количество заранее установлено (обычно 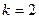 );
);
— последовательный — решение о принятии партии, забраковании или продолжении испытаний принимается после оценки каждой последовательно проверяемой единицы продукции (выборки или пробы).
Для сопоставления и оценки различных планов выборочного контроля служит оперативная характеристика - зависимость вероятности L принятия партии от доли дефектных единиц продукции  .
.
При сплошном контроле партии имеем идеальную оперативную характеристику (рис. 3.4, а), при которой принимаются все партии с  и бракуются все партии с
и бракуются все партии с 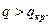 :
:

Оперативная характеристика  при выборочном контроле, показана на рис. 6, б. Чем ближе оперативная характеристика плана выборочного контроля к идеальной, тем план контроля лучше (обеспечивает большую уверенность в результатах). Однако с увеличением крутизны оперативной характеристики в средней ее части (между
при выборочном контроле, показана на рис. 6, б. Чем ближе оперативная характеристика плана выборочного контроля к идеальной, тем план контроля лучше (обеспечивает большую уверенность в результатах). Однако с увеличением крутизны оперативной характеристики в средней ее части (между 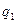 и
и 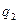 ) растет объем выборки, т. е. стоимость контроля. Поэтому обычно ищут компромиссное решение.
) растет объем выборки, т. е. стоимость контроля. Поэтому обычно ищут компромиссное решение.
    а) а) |  б) б) |
Рис. 3.4 Графики оперативных характеристик:
а – при 100% - ном контроле;
б – при выборочном контроле.
Основные понятия и определения теории испытаний статических гипотез
Чтобы проверить какую-либо гипотезу, имея выборку наблюдений, нужно разделить выборочное пространство на две области. Если наблюдается попадание выборочной точки 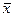 в одну из этих областей, скажем
в одну из этих областей, скажем 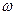 , то гипотеза отвергается, если же
, то гипотеза отвергается, если же 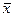 попадает в дополнительную область
попадает в дополнительную область  , то гипотеза принимается. Область
, то гипотеза принимается. Область 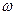 называется критической областью критерия, а
называется критической областью критерия, а  - областью принятия гипотезы.
- областью принятия гипотезы.
Если известно распределение вероятностей наблюдений, соответствующее проверяемой гипотезе 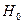 , то можно определить
, то можно определить 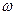 так, чтобы при выполнении гипотезы
так, чтобы при выполнении гипотезы 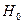 вероятность отвергнуть гипотезу (т.е. вероятность попадания
вероятность отвергнуть гипотезу (т.е. вероятность попадания 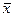 в
в 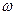 ) была равна заранее заданной величине
) была равна заранее заданной величине 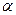 , т.е.
, т.е.
 . (3.1)
. (3.1)
Проверяемая гипотеза часто называется нулевой, а величина 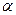 - уровнем значимости. Очевидно, в общем случае можно найти много подобластей, для которых выполняется равенство (3.1). Суждение о качестве критической области основывается на свойствах, которыми она обладает как в случае выполнения проверяемой гипотезы, так и в случае ее невыполнения. В связи с этим ошибки, возникающие при проверке статистической гипотезы, могут быть двух типов: 1) можно ошибочно отвергнуть гипотезу, когда она верна; 2) можно ее ошибочно принять, когда она не верна.
- уровнем значимости. Очевидно, в общем случае можно найти много подобластей, для которых выполняется равенство (3.1). Суждение о качестве критической области основывается на свойствах, которыми она обладает как в случае выполнения проверяемой гипотезы, так и в случае ее невыполнения. В связи с этим ошибки, возникающие при проверке статистической гипотезы, могут быть двух типов: 1) можно ошибочно отвергнуть гипотезу, когда она верна; 2) можно ее ошибочно принять, когда она не верна.
Эти ошибки называются соответственно ошибками первого и второго рода. Вероятность ошибки 1-ого рода (риск поставщика) равна 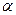 . Вероятность ошибки 2-ого рода (риск заказчика) обозначается
. Вероятность ошибки 2-ого рода (риск заказчика) обозначается 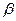 и зависит от альтернативы гипотезы
и зависит от альтернативы гипотезы 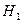 , т.е.
, т.е.
 , (3.2)
, (3.2)
или
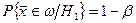 . (3.3)
. (3.3)
Вероятность 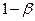 называется мощностью критерия для проверки гипотезы
называется мощностью критерия для проверки гипотезы 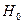 против альтернативной гипотезы
против альтернативной гипотезы 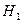 .
.
При разработке теории выборочного контроля для приема или браковки партии изделий массового производства Додж и Ромиг из лабораторий компании «Белл Телефон» около 1925 г. ввели понятие риска производства и риска потребителя. Их первые опубликованные результаты появились в 1929 г. [См. Додж и Ромиг (1929, 1959).] Эти понятия, по существу, были предшественниками рисков ошибки 1-ого и 2-ого рода. Именно, пусть с – доля дефектных изделий в партии из N изделий, а t – доля дефектных изделий в выборке объема n изделий из этой партии. При заданном значении q t будет случайной величиной с к.ф.р.  и со значениями 0,
и со значениями 0,  , …,
, …, 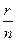 ,
,  , в интервале [0,1]. Множество значений параметра q состоит из точек 0,
, в интервале [0,1]. Множество значений параметра q состоит из точек 0,  , …,
, …,  интервала [0,1]. Заданное значение параметра
интервала [0,1]. Заданное значение параметра  определяет недопустимую долю дефектных изделий в партии, как значение
определяет недопустимую долю дефектных изделий в партии, как значение  , что соответствует
, что соответствует 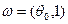 . Допустимая доля дефектных изделий (зона предпочтения) определяется значением
. Допустимая доля дефектных изделий (зона предпочтения) определяется значением  , так что
, так что  . Выберем теперь значения
. Выберем теперь значения  и критическое множество
и критическое множество  , так что при
, так что при 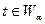 партия бракуется и
партия бракуется и 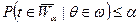 . Величина
. Величина 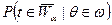 называется риском производства; это – вероятность того, что контролер забракует партию при допустимой доле
называется риском производства; это – вероятность того, что контролер забракует партию при допустимой доле  дефектных изделий в этой партии. Значение
дефектных изделий в этой партии. Значение  выбирается так, чтобы риск производства не превышал
выбирается так, чтобы риск производства не превышал 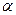 и приблизительно был равен
и приблизительно был равен 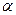 при
при  . Обычно на практике полагают
. Обычно на практике полагают 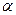 равным 0,05 или 0,10. Величина
равным 0,05 или 0,10. Величина 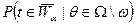 называют риском потребителя, она представляет собой вероятность того, что контролер примет партию, когда она содержит недопустимую долю дефектных изделий
называют риском потребителя, она представляет собой вероятность того, что контролер примет партию, когда она содержит недопустимую долю дефектных изделий  . На практике, если N достаточно велико, всегда можно выбрать n так, чтобы сделать риск потребителя сколь угодно малым для любого фиксированного значения доли дефектных изделий, превосходящего
. На практике, если N достаточно велико, всегда можно выбрать n так, чтобы сделать риск потребителя сколь угодно малым для любого фиксированного значения доли дефектных изделий, превосходящего  . Обычно объем выборки n подбирают так, чтобы риск потребителя
. Обычно объем выборки n подбирают так, чтобы риск потребителя 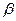 имел заданной значение (как правило 0,05 или0,10) при некотором
имел заданной значение (как правило 0,05 или0,10) при некотором  , немного превосходящим
, немного превосходящим  . Интервал (
. Интервал (  ,1) недопустимых значений
,1) недопустимых значений  разбивается на два множества: зону безразличия (
разбивается на два множества: зону безразличия (  ,
,  ) и зону отклонения (
) и зону отклонения (  ,1). Вероятность
,1). Вероятность  принять партию при доле дефектных изделий
принять партию при доле дефектных изделий  для заданного n будет функцией
для заданного n будет функцией  , ее обозначают
, ее обозначают  и называют оперативной характеристикой выборочного плана, определенного заданием объема выработки n и критической доле дефектных изделий
и называют оперативной характеристикой выборочного плана, определенного заданием объема выработки n и критической доле дефектных изделий  . Оперативная характеристика удовлетворяет условиям
. Оперативная характеристика удовлетворяет условиям 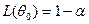 и
и 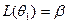 .
.
Вторым важным понятием, введенным Доджем и Ромигом (1929), было понятие предела среднего выходного качества. Он определяется как максимум по всем  среднего значения доли дефектных изделий в партии при условии, что в забракованных партиях все дефектные изделия заменены заведомо годными. При этом, конечно, предполагается неразрушительных характер проверки изделий, т. е. в процессе проверки изделие не разрушается.
среднего значения доли дефектных изделий в партии при условии, что в забракованных партиях все дефектные изделия заменены заведомо годными. При этом, конечно, предполагается неразрушительных характер проверки изделий, т. е. в процессе проверки изделие не разрушается.
Понятия ошибок 1-го и 2-го рода давно уже играют фундаментальную роль при отправлении правосудия; роль рисков ошибок 1-ог и 2-го рода здесь играют соответственно риски осуждения невиновного и оправдания виновного.
3.5 Метод Неймана – Пирсона (1933 г.)
