Вероятность попадания нормально распределенной случайной величины в заданный интервал

Вероятность попадания нормально распределенной с.в. в интервал определяется по формуле:

где – математическое ожидание, 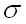– среднее квадратическое отклонение данной случайной величины.

И 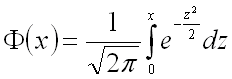– функция Лапласа.

Вероятность заданного отклонения нормально распределенной случайной величины от своего математического ожидания. Правило трех сигм.

Вероятность отклонения нормально распределенной с.в от математического ожидания по
абсолютной величине меньше, чем на 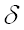( 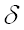>0), определяется по формуле:

где – математическое ожидание, 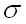– среднее квадратическое отклонение.

Вычислим вероятность того, что отклонение нормально распределенной случайной величины от своего математического ожидания по абсолютной величине не превысит .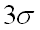
Воспользуемся формулой для нахождения вероятности заданного отклонения, в которую в качестве 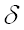подставим :
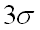Таким образом, вероятность того, что отклонение

случайной величины по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит 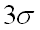, составляет всего 0,0027. Такое событие, исходя их принципа невозможности маловероятных событий, можно считать практически невозможным.
Вывод (правило трех сигм): если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

52. Закон больших чисел: неравенство Чебышева.

Под «законом больших чисел» в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

В основе- неравенство Чебышева:

Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше чем :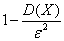

Справедливо для дискретных и непрерывных с.в.

Теорема Чебышева.

Пусть имеется бесконечная последовательность независимых случайных величин с одним и тем же математическим ожиданием и дисперсиями, ограниченными одной и той же постоянной С:

Тогда каково бы ни было положительное число вероятность события стремится к единице.

Теорема Бернулли.

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р.