Ряд, образованный геометрической прогрессией

Необходимое условие сходимости ряда.

Гармонический ряд

Теоремао необходимом условии сходимости ряда.

Если ряд 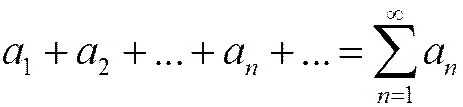сходится, то предел последовательности общих членов этого ряда равен нулю:

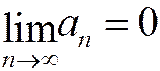. (1.11)

Другая формулировка. Для того чтобы ряд сходился, необходимо (но недостаточно!), чтобы предел последовательности общих членов ряда был равен нулю.

Замечание.Иногда для краткости слово «последовательность» опускают и говорят: «предел общего члена ряда равен нулю». То же для последовательности частичных сумм («предел частичной суммы»).

Доказательство теоремы. Представим общий член ряда в виде (1.10):

.

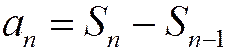По условию ряд сходится, следовательно, 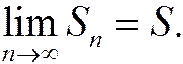Очевидно, что и 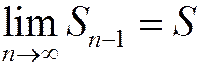, т.к. п и п-1 стремятся к бесконечности одновременно . Найдем предел последовательности общих членов ряда:

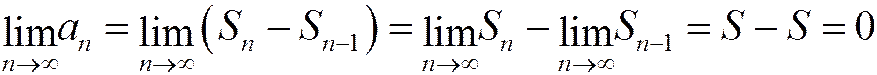, ч.т.д.

Замечание.Обратное утверждение неверно. Ряд, удовлетворяющий условию (1.11), не обязательно сходится. Поэтому условие, или признак (1.11) является необходимым, но не является достаточным признаком сходимости ряда.

Пример 1. Гармонический ряд. Рассмотрим ряд

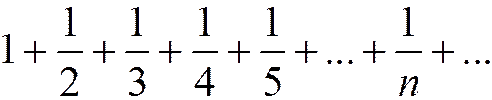(1.12)

Этот ряд называется гармоническим, т.к. каждый его член, начиная со второго, является средним гармоническим соседних с ним членов:

.

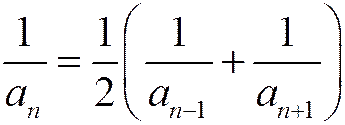Например:

Рис.1.3.1 Рис.1.3.2

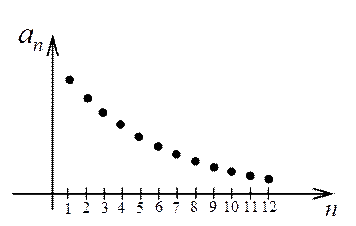
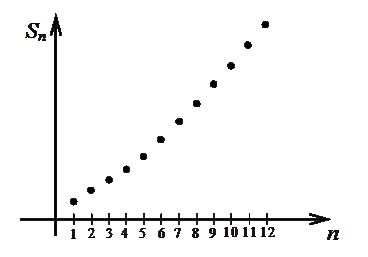
Общий член гармонического ряда удовлетворяет необходимому условию сходимости ряда (1.11): 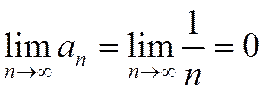(рис.1.3.1). Однако в дальнейшем будет показано (с помощью интегрального признака Коши), что этот ряд расходится, т.е. его сумма равна бесконечности. На рис.1.3.2 показано, что частичные суммы неограниченно возрастают при увеличении номера.

Следствие. Из необходимого условия сходимости ряда вытекает достаточный признак расходимости ряда: если 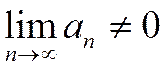или не существует, то ряд расходится.

Доказательство. Предположим противное, т.е. 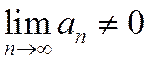(или не существует), но ряд сходится. Но согласно теореме о необходимом условии сходимости ряда предел общего члена должен быть равен нулю: 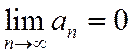. Противоречие.

Пример 2. Исследовать на сходимость ряд с общим членом .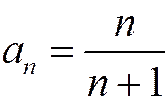

Данный ряд имеет вид: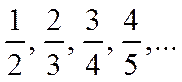

Найдем предел общего члена ряда:

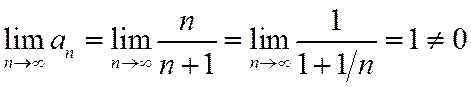. Согласно следствию данный ряд расходится.

Ряд, образованный геометрической прогрессией

Рассмотрим ряд, составленный из членов геометрической прогрессии. Напомним, что геометрической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число, не равное нулю и называемое знаменателем этой прогрессии. Геометрическая прогрессия имеет вид:

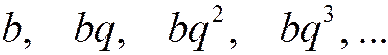
а ряд, составленный из ее членов:

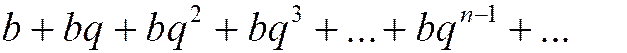
Такой ряд называется геометрическим рядом, но иногда для краткости его называют просто геометрической прогрессией. Название «геометрическая» прогрессия получила потому, что каждый ее член, начиная со второго, равен среднему геометрическому соседних с ним членов:

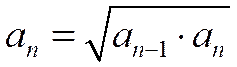, или .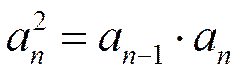

Теорема. Ряд, составленный из членов геометрической прогрессии

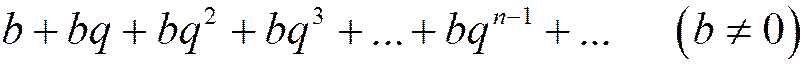(1.13)

расходится при 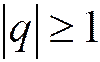и сходится при 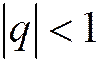, причём при 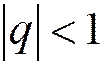сумма ряда

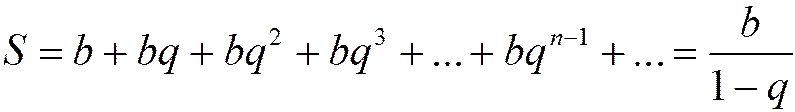(1.14)

Доказательство. Общий член ряда, как и общий член геометрической прогрессии, имеет вид: .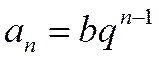

1) Если 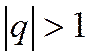, то 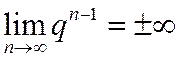, т.к. в этом случае 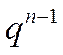– бесконечно большая величина.

2) При 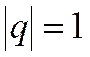ряд ведёт себя по-разному, т.к. приобретает различные виды.

При ;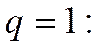

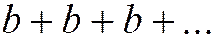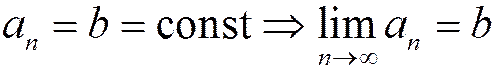, т.к. предел константы равен самой константе. Т.к. по условию теоремы 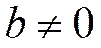, общий член ряда не стремится к нулю.

При 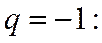; предела не существует.

Таким образом, при 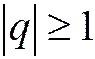не выполняется необходимое условие сходимости ряда:

.

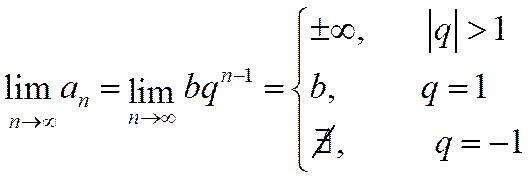Следовательно, ряд (1.13) расходится.

3) Если 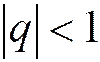, то прогрессия называется бесконечно убывающей. Из школьного курса известно, что n-ю частичную сумму ряда (1.13) можно представить в виде:

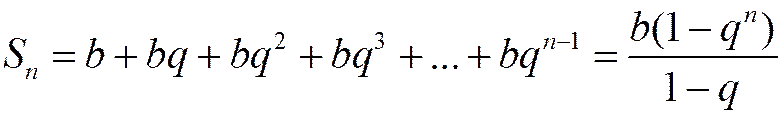. (1.15)

Найдём сумму ряда. Так как при 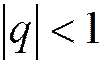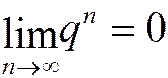(бесконечно малая величина), то

.

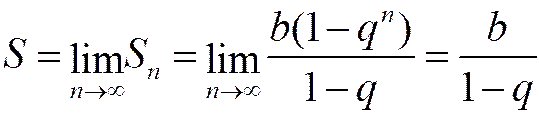Таким образом, при 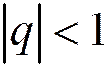ряд (1.13) сходится и имеет сумму, равную

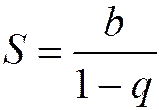. (1.16)

Это и есть сумма бесконечно убывающей геометрической прогрессии.

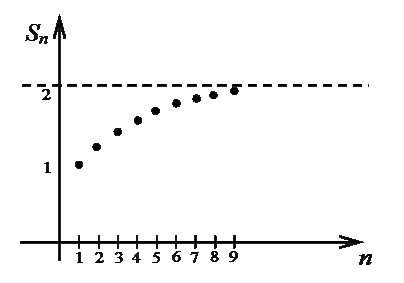
Пример 1º.

Рис.1.4.1

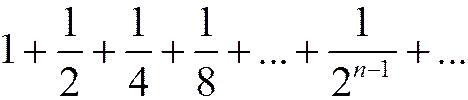=2.

Оценим его сумму, т.е. попробуем определить, к чему стремится последовательность его частичных сумм.

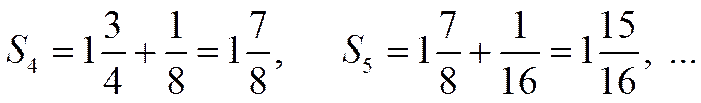
Видно, что последовательность частичных сумм стремится к числу 2 (рис.1.4.1).

А теперь докажем это. Воспользуемся тем, что данный ряд - это ряд, составленный из членов геометрической прогрессии, где 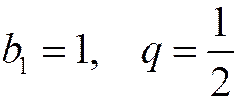. Сумма бесконечно убывающей геометрической прогрессии

.

Пример 2º.

.

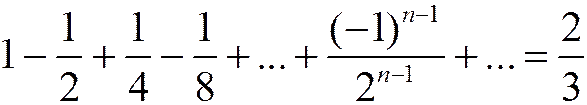Вычисляется аналогично. Поскольку многие из членов ряда в отличие от предыдущего примера имеют знак минус, то сумма оказалась меньше.

Пример 3º.

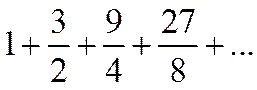
Это геометрический ряд, где 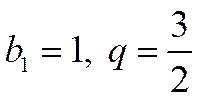>1. Такой ряд расходится.

Свойства сходящихся рядов

Рассмотрим два сходящихся ряда:

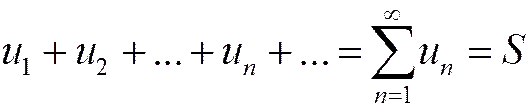, (1.17)

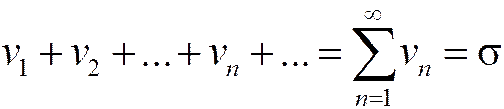. (1.18)

1. Ряд, полученный почленным сложением (вычитанием) двух сходящихся рядов, также сходится, а его сумма равна алгебраической сумме исходных рядов, т.е.

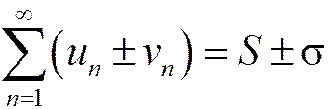. (1.19)

Доказательство.Составим частичные суммы рядов (1.17) и (1.18):

.

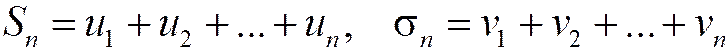Т.к. по условию данные ряды сходятся, существуют пределы этих частичных сумм:

, .

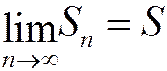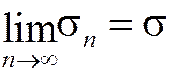Составим частичную сумму ряда (1.19) и найдём её предел:

;

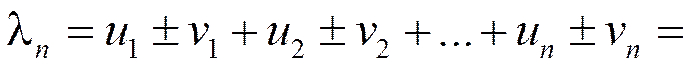
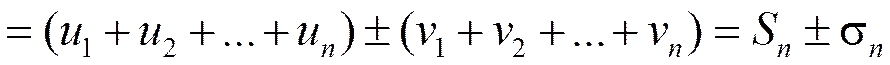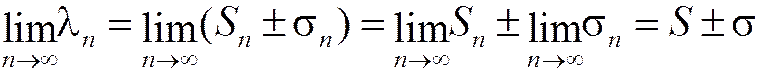, ч.т.д.

Пример.

;

.

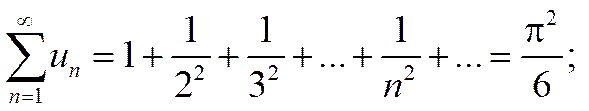
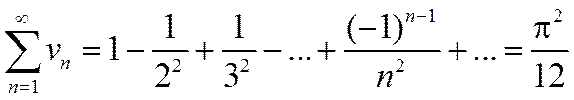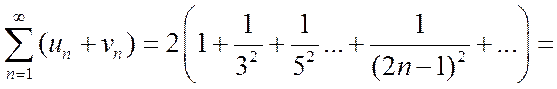
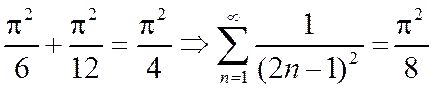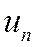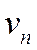Замечание. Обратное утверждение неверно, т.е. из сходимости ряда, стоящего в левой части равенства (1.19), не следует сходимость рядов и . Например, ряд, рассмотренный в примере 4, сходится, и его сумма равна 1; общий член этого ряда был преобразован к виду:

.

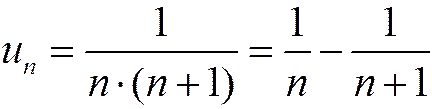Следовательно, ряд можно записать в виде:

.

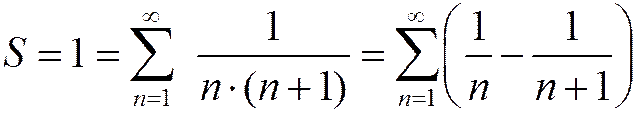Рассмотрим теперь отдельно ряды:

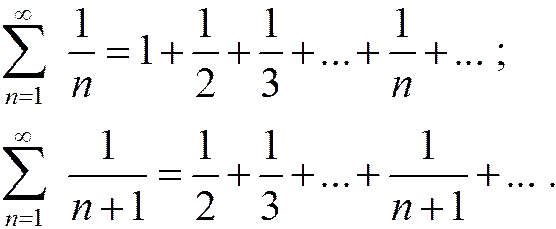
Эти ряды расходятся, так как являются гармоническими рядами. Таким образом, из сходимости алгебраической суммы рядов не следует сходимость слагаемых.

2. Если все члены сходящегося ряда с суммой S умножить на одно и то же число с, то полученный ряд также будет сходиться и иметь сумму cS:

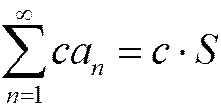. (1.20)

Доказательство аналогично первому свойству (доказать самостоятельно).

Пример. с=10000;

.

Оба ряда сходятся, т.к. их суммы конечны.

Таким образом, сходящиеся ряды можно почленно складывать, вычитать и умножать на постоянный множитель.

3. Теорема об отбрасывании нескольких первых членов ряда.

Отбрасывание (или добавление) нескольких первых членов ряда не влияет на сходимость или расходимость этого ряда. Иными словами, если сходится ряд

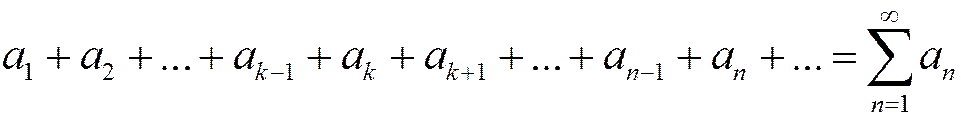, (1.21)

то сходится и ряд

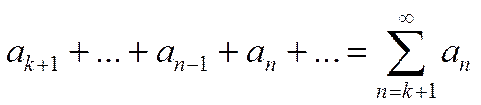. (1.22)

(но сумма может быть другой). И наоборот, если сходится ряд (1.22), то сходится и ряд (1.21).

Замечание 1. В математике термин «несколько» означает «конечное число», т.е. это может быть и 2, и 100, и 10¹⁰⁰, и больше.

Замечание 2. Из данного свойства следует, что ряды с общими членам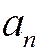и и 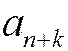эквивалентны в смысле сходимости. Например, гармонический ряд имеет общий член 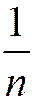, и ряды с общими членам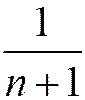и и 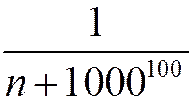- также гармонические.

4. Остаток ряда. Его свойство. Если у ряда отбросить первые k членов, то получится новый ряд, называемый остатком ряда после k-го члена.

Определение. k-м остатком ряда

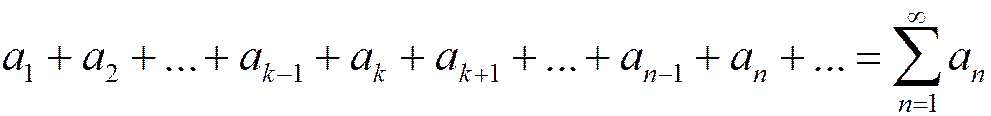
называется ряд

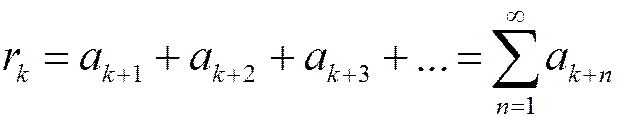(1.23),

полученный отбрасыванием первых k членов исходного ряда.

Индекс k означает, сколько первых членов ряда отброшено. Таким образом,

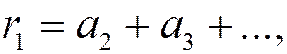
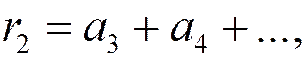
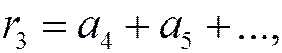и т.д.

Рис.1.5.2

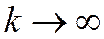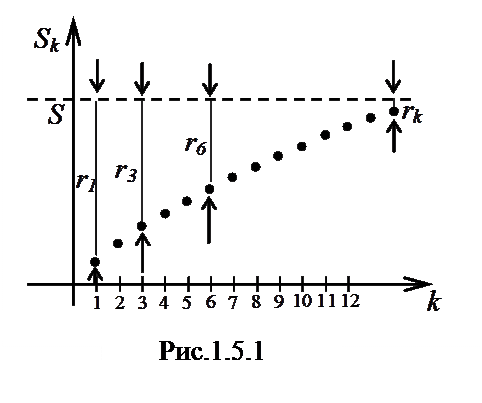
Можно построить последовательность остатков и исследовать её на сходимость при , в отличие от предыдущей теоремы, где к бесконечности стремилось п. В каждом последующем члене этой последовательности «меньше» слагаемых (на самом деле в каждом остатке их бесконечное число). Можно также сказать, что здесь имеет место динамика в начале ряда, а не в его конце.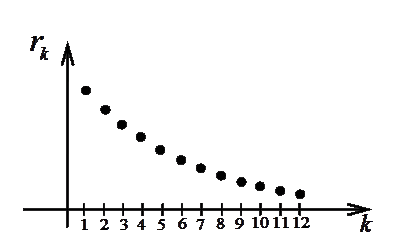

Остаток ряда можно определить также как разность между суммой ряда и его частичной суммой (рис.1.5.1):

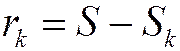. (1.24)

Рис.1.5.2

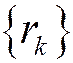Найдём предел последовательности для сходящегося ряда с суммой S при 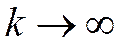. Из определения суммы ряда следует:

.

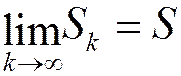Тогда из (1.24) следует:

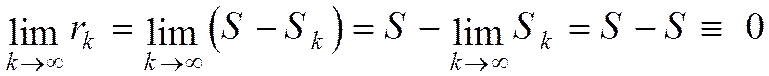. (1.25)

Получили, что остаток сходящегося ряда есть величина бесконечно малая при 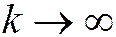, т.е. когда число отбрасываемых членов ряда стремится к бесконечности. Это видно и из рисунков 1.5.1 и 1.5.2.

Замечание.Теорему об отбрасывании нескольких членов ряда можно сформулировать следующим образом: для того, чтобы ряд сходился, необходимо и достаточно, чтобы его остаток стремился к нулю.

§1.6. Знакоположительные ряды

Рассмотрим ряд с неотрицательными членами

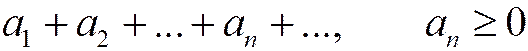, (1.26)

Такие ряды будем называть знакоположительными. Рассмотрим последовательность частичных сумм 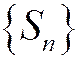знакоположительного ряда (1.26). Поведение этой последовательности особенно простое: она монотонно возрастает при возрастании n, т.е. 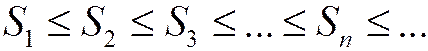. (т.к. к каждой последующей частичной сумме прибавляется неотрицательное число).

Согласно теореме Вейерштрасса любая монотонная ограниченная последовательность сходится (см. I семестр I курса). Исходя из этого, сформулируем общий критерий сходимости рядов с положительными членами.

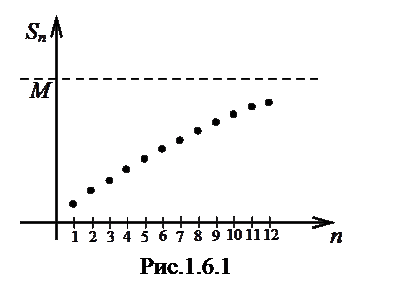
Теорема(общий критерий сходимости знакоположительных рядов). Для того, чтобы знакоположительный ряд сходился, необходимо и достаточно, чтобы последовательность его частичных сумм 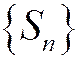была ограничена.

Напомним определение ограниченности последовательности: последовательность называется ограниченной, если существует М>0 такое, что для 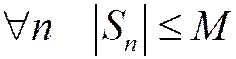(рис.1.6.1). Для знакоположительных рядов 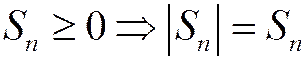, и можно говорить об ограниченности сверху, т.к. снизу 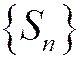ограничена нулём.

Доказательство. 1) Необходимость. Пусть ряд (1.26) сходится Þ последовательность частичных сумм имеет предел, т.е. сходится. По теореме об ограниченности сходящейся последовательности любая сходящаяся последовательность ограничена Þ 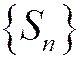ограничена.

2) Достаточность. Пусть последовательность частичных сумм ряда (1.26) ограничена.

Т.к. 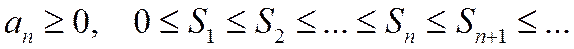, т.е. 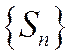монотонна. По теореме Вейерштрасса о монотонных ограниченных последовательностях она сходится Þ сходится ряд (1.26).

Ясно, что при неограниченном возрастании последовательности частичных сумм 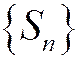ряд расходится.

Общий критерий сходимости знакоположительных рядов позволяет установить достаточные признаки сходимости рядов с положительными членами. Этими признаками являются:

1) признаки сравнения рядов;

2) признак Даламбера;

3) признаки Коши.

Первый признак сравнения

Теорема о первом признаке сравнения.

Пусть даны два ряда с неотрицательными членами:

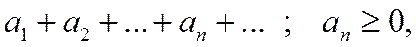(1.27)

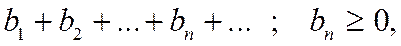(1.28)

причем, начиная с некоторого номера n³N,выполняется неравенство

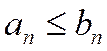. (1.29)

Тогда:

1) из сходимости ряда (1.28) следует сходимость ряда (1.27);

2) из расходимости ряда (1.27) следует расходимость ряда (1.28).

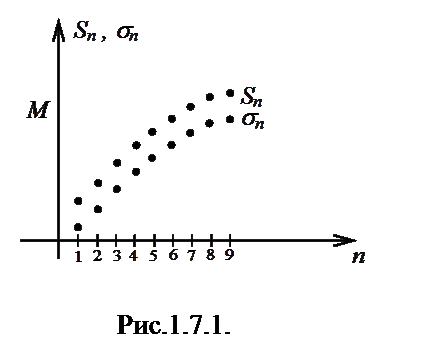Другими словами, если сходится больший ряд, то сходится и меньший, если расходится меньший ряд, то больший расходится и подавно (рис.1.7.1).

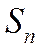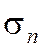Доказательство. 1) Пусть и - частичные суммы рядов (1.27) и (1.28), соответственно. Т.к. 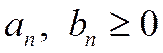, из соотношения (1.29) следует, что 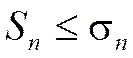(сумма меньших чисел меньше суммы больших чисел). Если ряд 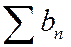сходится, то последовательность его частичных сумм 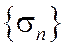ограничена (сверху), но тогда ограничена и последовательность частичных сумм 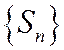ряда 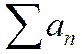как ряда с меньшими членами; Þ согласно общему критерию сходимости ряд 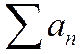сходится.

2) Пусть теперь ряд 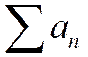расходится. Предположим, что при этом ряд 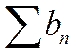сходится. Но тогда по только что доказанному меньший ряд 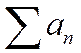также должен сходиться. Противоречие. Следовательно, ряд 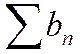расходится.

Признак сравнения применяется для исследования сходимости знакоположительных рядов, если известна сходимость какого-либо другого ряда, годного для сравнения с заданным рядом. Чаще всего сравнивают с геометрической прогрессией (сходится при 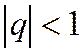и расходится при 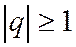) и с обобщённым гармоническим рядом 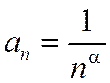, который сходится при a>1 и расходится при a£1 (доказательство будет приведено позже).

Пример 1.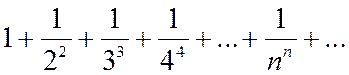

Сравним данный ряд с бесконечной геометрической прогрессией:

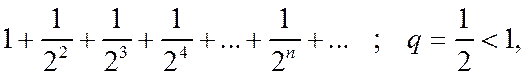которая сходится.

Так как начиная с n=3 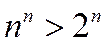Þ 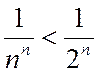, то данный ряд сходится.

Пример 2.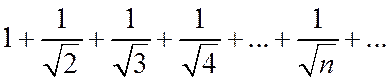

Сравним данный ряд с расходящимся гармоническим рядом .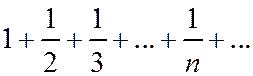

Так как начиная с п=2 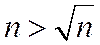Þ 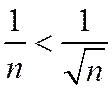, то данный ряд расходится.

Замечание. Данный ряд является обобщенным гармоническим рядом, 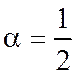.