Переместительное свойство сходящихся рядов
Фразу «от перемены мест слагаемых сумма не меняется» в школе так вбивают в голову, что она кажется аксиомой. Она действительно верна, если слагаемых конечноечисло. Но будет ли она верна, если слагаемых бесконечно много? Ответу на этот вопрос и посвящены две следующие теоремы.
Пусть дан сходящийся ряд 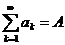 (ряд А). Пусть
(ряд А). Пусть 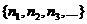 есть некоторая перестановка чисел
есть некоторая перестановка чисел 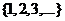 , причем чисел переставлено бесконечно много. Рассмотрим ряд
, причем чисел переставлено бесконечно много. Рассмотрим ряд 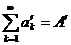 (ряд
(ряд 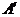 ), где
), где 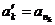 . Будет ли выполняться равенство
. Будет ли выполняться равенство 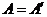 ?
?
Теорема. Если ряд А сходится абсолютно, то ряд А’ тоже абсолютно сходится и имеет ту же сумму.
Доказательство.
1. Пусть 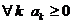 и
и 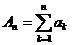 есть частная сумма рада А. Так как все слагаемые неотрицательны, то, очевидно, все частные суммы меньше суммы ряда А.
есть частная сумма рада А. Так как все слагаемые неотрицательны, то, очевидно, все частные суммы меньше суммы ряда А.
Рассмотрим теперь частные суммы ряда 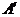 :
:
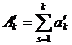 .
.
Возьмем 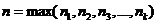 . Тогда очевидно, что
. Тогда очевидно, что 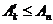 , так как в сумме
, так как в сумме 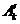 не большеслагаемых, чем в сумме
не большеслагаемых, чем в сумме 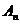 . Но
. Но 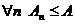 , и поэтому
, и поэтому 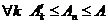 и ряд
и ряд 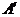 сходится. При этом верно соотношение
сходится. При этом верно соотношение 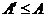 .
.
Но ряд А также получается из ряда 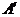 перестановкой слагаемых. Поэтому должно одновременно выполняться и неравенство
перестановкой слагаемых. Поэтому должно одновременно выполняться и неравенство 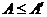 . Отсюда и следует, что
. Отсюда и следует, что 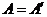 .
.
2. Пусть теперь слагаемые ряда А могут иметь произвольный знак, но ряд, составленный из их модулей, сходится: 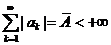 .
.
Основная идея дальнейшего состоит в том, чтобы разбить ряд А на два ряда, в одном их которых будут собраны все положительные слагаемые, а в другом - все отрицательные. Представим себе, что мы просматриваем все слагаемые ряда А по порядку номеров. Если окажется, что 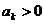 , то обозначим его через
, то обозначим его через 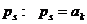 (величины
(величины 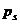 нумеруются в порядке их появления). Если окажется, что
нумеруются в порядке их появления). Если окажется, что 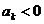 , то введем величину
, то введем величину 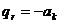 (величины
(величины 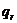 также нумеруются в порядке их появления. Таким образом, вместо одного ряда А появятся два ряда
также нумеруются в порядке их появления. Таким образом, вместо одного ряда А появятся два ряда 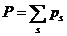 и
и 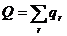 .
.
Так как 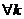 частные суммы этих рядов удовлетворяют неравенствам
частные суммы этих рядов удовлетворяют неравенствам 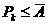 ,
, 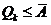 , то оба этих ряда сходятся. Далее очевидно, что
, то оба этих ряда сходятся. Далее очевидно, что 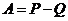 и
и 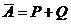 .
.
Но перестановка слагаемых в ряде А приведет лишь к перестановке слагаемых в рядах P и Q. Все слагаемые этих рядов положительные, следовательно, согласно п.1, от такой перестановки их суммы не изменятся, а поэтому не изменится сумма ряда А. <
Итак, в абсолютно сходящихся рядах от перестановки слагаемых из сумма не меняется. А как насчет неабсолютно сходящихся рядов?
Теорема Римана. Если ряд 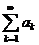 сходится неабсолютно, то, какое бы ни взять число В (конечное, или равное ± ¥), можно так переставить слагаемые в ряде, что его сумма станет равной В.
сходится неабсолютно, то, какое бы ни взять число В (конечное, или равное ± ¥), можно так переставить слагаемые в ряде, что его сумма станет равной В.
Так что от перестановки местами слагаемых сумма все-таки может меняться!
Доказательство.
1. Проделаем с нашим рядом ту же процедуру, что и в предыдущей теореме, и построим ряды P и Q. Но теперь ситуация меняется кардинально: 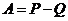 есть конечное число, а
есть конечное число, а 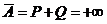 . Это может быть лишь в том случае, когда
. Это может быть лишь в том случае, когда 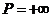 и
и 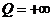 , то есть ряды P и Q расходящиеся.
, то есть ряды P и Q расходящиеся.
2. Возьмем конечное число В. Пусть, для определенности, 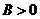 . Начнем строить новый ряд
. Начнем строить новый ряд 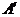 следующим образом.
следующим образом.
Начнем сначала складывать положительные слагаемые из ряда Р. Так как этот ряд расходящийся, то есть его сумма равна + ¥, то на каком-то шаге накопленная сумма превзойдет число В. Мы остановимся, как только это произойдет в первый раз, то есть будет выполнено следующее
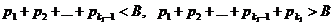 .
.
А теперь начнем прибавлять отрицательные слагаемые ряда А, то есть вычитать слагаемые ряда Q. Сумма этого ряда также равна + ¥, и поэтому на каком-то шаге накопленная сумма обязательно станет меньше В. Мы снова остановимся, как только это произойдет в первый раз, то есть будет выполнено следующее
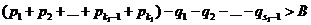 ,
,
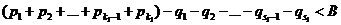 .
.
Снова начнем прибавлять положительные слагаемые, пока накопленная сумма не превзойдет В, затем снова отрицательные, пока накопленная сумма не станет меньше В, и т.д. и т.д.
Эту процедуру можно проиллюстрировать следующим рисунком:
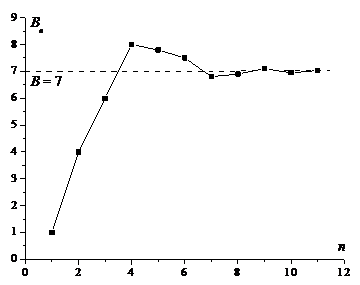 | Каждый раз членов рядов P и Q берется не больше, чем необходимо для первого осуществления требуемого неравенства. Тогда отклонения накопленных сумм от В по модулю не превысят последнего написанного члена. В силу сходимости ряда А его общий член стремится к нулю. Следовательно, накопленные суммы стремятся к числу В, так что построенный ряд сходится и его сумма равна именно В. |
3. Пусть 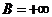 .
.
Возьмем последовательность чисел 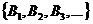 , такую, что
, такую, что
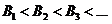 ,
, 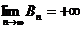 .
.
Трудность заключается в том, что нам надо разместить не только положительные, но и отрицательные члены ряда. Поэтому поступаем следующим образом:
Сначала складываем положительные слагаемые до тех пор, пока их сумма в первый разне превысит число В1:
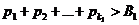 .
.
Затем добавляем одноотрицательное слагаемое и снова добавляем положительные, пока их сумма в первый разне превысит число В2:
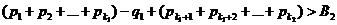 .
.
Снова добавляем одно отрицательное слагаемое и снова добавляем положительные, пока их сумма в первый разне превысит число В3 и т.д. Так как чисел 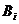 счетное множество, то разместятся не только все положительные, но и все отрицательные слагаемые.
счетное множество, то разместятся не только все положительные, но и все отрицательные слагаемые.
Очевидно, что сумма построенного таким образом ряда равна + ¥. <
Пример.
Рассмотрим ряд
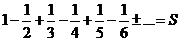 ,
,
который сходится по признаку Лейбница. Переставим его слагаемые по следующему правилу: после положительного слагаемого идут два отрицательных:
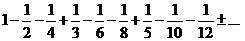 .
.
Из экономии, мы не будем доказывать, что этот ряд сходится - попробуйте сделать это сами.
Каждая тройка слагаемых имеет следующую структуру
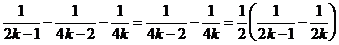 ,
,
Тогда построенный ряд принимает вид
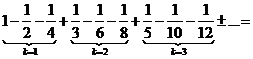
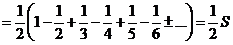 ,
,
так что сумма построенного ряда уменьшилась в два раза.
Таким образом, в неабсолютно сходящемся ряде можно переставлять местами только конечноечисло слагаемых, а вот переставлять местами бесконечноечисло слагаемых нельзя - можно получить все, что угодно.
Перемножение рядов
Пусть даны два ряда
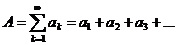 (ряд А) и
(ряд А) и
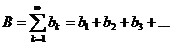 (ряд В).
(ряд В).
Как определить произведение этих рядов?
Рассмотрим бесконечную матрицу
 ,
,
составленную из всевозможных произведений вида  . Нам надо сложить все элементы этой матрицы. Как это сделать? Моно, например, по диагоналям складывать
. Нам надо сложить все элементы этой матрицы. Как это сделать? Моно, например, по диагоналям складывать
 , (*)
, (*)
а можно и так
 ,
,
можно еще тысячами разных способов. Но где гарантия, что все эти ряды имеют одну и ту же сумму?
Теорема Коши. Если ряды (А) и (В) сходятся абсолютно, то их произведение, составленное из слагаемых вида  , взятых в любом порядке, также сходится и имеет своей суммой
, взятых в любом порядке, также сходится и имеет своей суммой 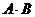 .
.
Доказательство.
Рассмотрим ряд вида
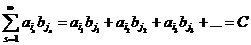
в которое входят все комбинации типа  , и рассмотрим его частную сумму
, и рассмотрим его частную сумму
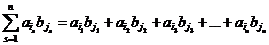 .
.
Пусть 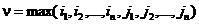 . Тогда
. Тогда
 ,
,
где  ,
, 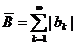 . Следовательно, ряд
. Следовательно, ряд 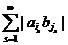 сходится. В силу этого ряд
сходится. В силу этого ряд  сходится абсолютно и поэтому его слагаемые можно располагать в любом порядке. Беря частные суммы ряда С в виде
сходится абсолютно и поэтому его слагаемые можно располагать в любом порядке. Беря частные суммы ряда С в виде
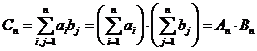
и поэтому 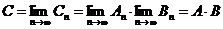 . <
. <
на практике чаще всего суммируют по диагоналям бесконечной матрицы, как в (*).
Двойные ряды
Обобщением рассмотренной выше ситуации является следующая. Дана бесконечная матрица
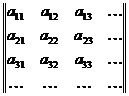 .
.
Рассмотрим суммы  . Рассмотрим двойной предел, когда m и n одновременно независимо друг от друга стремятся в + ¥ (более строгое определение понятия двойного предела смотрите в следующей главе):
. Рассмотрим двойной предел, когда m и n одновременно независимо друг от друга стремятся в + ¥ (более строгое определение понятия двойного предела смотрите в следующей главе):
 ,
,
который называется двойным рядом, и обозначается символом 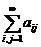 .
.
Кроме этого можно рассмотреть и так называемые повторные пределы, когда в + ¥ уходит сначала n, а потом т
 ,
,
или, наоборот, сначала т, а потом п
 .
.
Они называются повторными рядами.
Теорема. Если из трех рядов
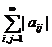 ,
, 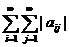 ,
, 
то сходятся и два остальные и верно равенство
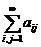 =
= 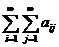 =
= 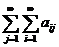 .
.
Доказательство.
1. Пусть  . Тогда очевидно, что
. Тогда очевидно, что 
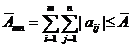 . Но
. Но  монотонно возрастает с ростом п, и, в силу ограниченности сверху, существует конечный предел
монотонно возрастает с ростом п, и, в силу ограниченности сверху, существует конечный предел 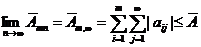 .
.
Но  также монотонно возрастает с ростом т, и также ограничена сверху. Поэтому существует и повторный предел
также монотонно возрастает с ростом т, и также ограничена сверху. Поэтому существует и повторный предел
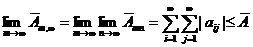
и ряд 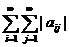 сходится. Совершенно аналогично показывается сходимость ряда
сходится. Совершенно аналогично показывается сходимость ряда  .
.
2. Пусть теперь  . Тогда
. Тогда 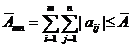 . Но
. Но  монотонно возрастают с ростом п и т, и, в силу ограниченности
монотонно возрастают с ростом п и т, и, в силу ограниченности  сверху, существует двойной предел
сверху, существует двойной предел  .
.
3. Сравнивая полученные неравенства легко получить, что суммы всех этих трех рядов равны между собой
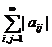 =
= 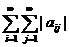 =
=  .
.
Но тогда ряды
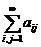 ,
, 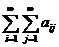 ,
, 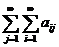 .
.
Сходятся абсолютно, и, в силу этого, в них можно произвольно переставлять слагаемые, их суммы от этого не изменятся. Поэтому
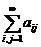 =
= 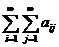 =
= 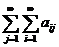 . <
. <
Бесконечные произведения
В заключение этой главы рассмотрим коротко достаточно экзотический раздел математического анализа - так называемые бесконечные произведения.
Определения.
Пусть имеем последовательность вещественных чисел  , которые все отличны от нуля.Рассмотрим так называемые частные произведения
, которые все отличны от нуля.Рассмотрим так называемые частные произведения
 ;
;  ;
; 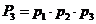 ; …
; …  .
.
Предел  называется бесконечным произведением. Если этот предел существует, конечен и отличен от нуля, то говорят, что бесконечное произведение сходится, в противном случае - расходится.
называется бесконечным произведением. Если этот предел существует, конечен и отличен от нуля, то говорят, что бесконечное произведение сходится, в противном случае - расходится.
Величина  называется остаточным произведением после п-го сомножителя.
называется остаточным произведением после п-го сомножителя.
Свойства
1. Если бесконечное произведение сходится, то " п сходится и остаточное произведение. Наоборот, если какое-то остаточное произведение сходится, то сходится и само бесконечное произведение и верна формула

Доказательство.
А) Пусть существует 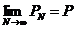 . Но тогда
. Но тогда 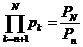 и, делая предельный переход N ® ¥, получим
и, делая предельный переход N ® ¥, получим
 .
.
Б) Пусть существует  . Но тогда
. Но тогда 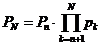 и поэтому
и поэтому 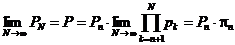 .
.
2. Если бесконечное произведение сходится, то 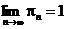 .
.
Действительно,  и поэтому
и поэтому 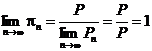 .
.
3. Если бесконечное произведение сходится, то  .
.
Действительно, 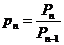 и поэтому
и поэтому  .
.
Следствие. Если бесконечное произведение сходится, то, начиная с некоторого N, все 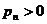 .
.
Этими простейшими свойствами мы ограничимся.
Признаки сходимости
Теорема 1. для того, чтобы бесконечное произведение сходилось необходимо и достаточно, чтобы сходился ряд  .
.
Доказательство.
Имеем
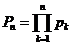 ;
;  ;
; 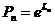 .
.
Используя непрерывность логарифмической и показательной функций, получаем:
А) 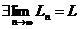 Þ
Þ 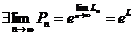 .
.
Б) 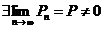 Þ
Þ 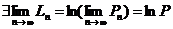 . <
. <
Так как  , то представим
, то представим 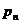 в виде
в виде  . Тогда
. Тогда 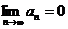 .
.
Теорема 2. Пусть, начиная с некоторого N, все 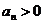 . Тогда, для сходимости бесконечного произведения необходимо и достаточно, чтобы сходился ряд
. Тогда, для сходимости бесконечного произведения необходимо и достаточно, чтобы сходился ряд 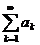 .
.
Доказательство.
Так как 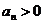 ,то
,то 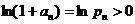 . Далее, так как
. Далее, так как 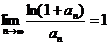 , то ряды
, то ряды 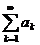 и
и 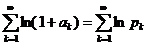 сходятся или расходятся одновременно. <
сходятся или расходятся одновременно. <
Теорема 3. Из сходимости рядов 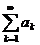 и
и  следует сходимость бесконечного произведения.
следует сходимость бесконечного произведения.
Доказательство.
Примем без доказательства неравенство 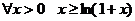 . Можете попытаться доказать его сами.
. Можете попытаться доказать его сами.
Далее, применяя правило Лопиталя, легко получить, что
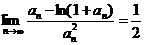 .
.
Далее идет следующая цепочка следований:
Ряд  сходится Þ ряд
сходится Þ ряд  также сходится. Но так как сходится ряд
также сходится. Но так как сходится ряд 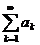 , то сходится и ряд
, то сходится и ряд 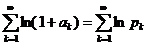 Þ бесконечное произведение сходится. <
Þ бесконечное произведение сходится. <
Еще кое-что
Бесконечное произведение  называется абсолютно сходящимся, если
называется абсолютно сходящимся, если 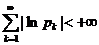 . Если ряд
. Если ряд 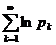 сходится, но
сходится, но  , то бесконечное произведение
, то бесконечное произведение  называется неабсолютно сходящимся
называется неабсолютно сходящимся
В абсолютно сходящемся произведении можно как угодно переставлять сомножители - от этого оно не изменится. В неабсолютно сходящемся произведении перестановка сомножителей может изменить значение бесконечного произведения.
