Простейшие свойства сходящихся рядов
Глава 9. Числовые ряды
Определения
Пусть дана последовательность вещественных чисел 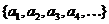 . Образуем новую последовательность по правилу
. Образуем новую последовательность по правилу
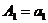 ;
;  ;
; 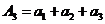 ; … ;
; … ; 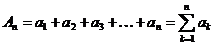 .
.
Эти величины называются частными суммамичислового ряда, а слагаемое 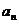 называют общим членомряда.
называют общим членомряда.
Рассмотрим теперь 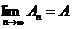 . Он называется числовым рядоми обозначается символом
. Он называется числовым рядоми обозначается символом
 .
.
Если этот предел существует и конечен, то говорят, что числовой ряд сходится, а само значение предела, то есть величину А, называют суммойчислового ряда. Если этот предел не существует или бесконечен, то говорят, что числовой ряд расходится(так как в данной главе других рядов не будет, то слово «числовой» мы будем опускать).
Обратите внимание на одну деталь: индекс суммирования в знаке бесконечной суммы может быть любым, то есть
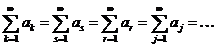 ,
,
от этого ничего не меняется. Как говорят, индекс суммирования является немым индексом,то есть он может быть обозначен любой буквой.
Величина

называется остатком ряда после n-го слагаемого.Его можно записать и так:
 .
.
Простейшие свойства сходящихся рядов
1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости остатка вытекает сходимость исходного ряда.
Доказательство.
Имеем:
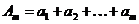
- частная сумма исходного ряда и

- частная сумма остатка ряда после п-го слагаемого. Очевидно, что между этими величинами имеет место соотношение
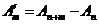
Если ряд сходится Þ  Þ
Þ 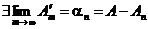 Þ остаток ряда после п-го слагаемого.
Þ остаток ряда после п-го слагаемого.
Далее, 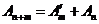 , и поэтому
, и поэтому
Если сходится остаток ряда после п-го слагаемого Þ 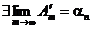 Þ
Þ  Þ исходный ряд сходится.
Þ исходный ряд сходится.
Обратите внимание на важное для дальнейшего соотношение 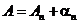 .
.
Следствие. Отбрасывание или изменение конечногочисла членов ряда не изменяет его сходимости.
2. Если ряд 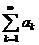 сходится, то
сходится, то  .
.
Действительно, из соотношения 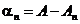 получаем
получаем
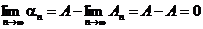 .
.
3. Если ряд 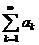 сходится, то его общий член стремится к нулю, то есть
сходится, то его общий член стремится к нулю, то есть 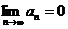 .
.
Действительно, из определения частных сумм легко видеть, что 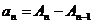 . Поэтому
. Поэтому
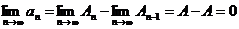
Следствие. (важно!)Признак расходимостиряда.
Если общий член ряда не стремится к нулю, то ряд расходится.
4. Если ряд 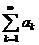 сходится, то ряд
сходится, то ряд 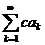 тоже сходится и верно соотношение
тоже сходится и верно соотношение
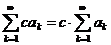 . Действительно, для частных сумм наших рядов имеем
. Действительно, для частных сумм наших рядов имеем
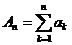 ;
; 
Делая предельный переход  , получаем
, получаем
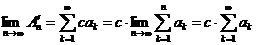 .
.
5. Если ряды 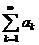 и
и  сходятся, то ряд
сходятся, то ряд 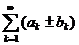 тоже сходится и верно соотношение
тоже сходится и верно соотношение
 .
.
Действительно, из определения частных сумм рядов получаем
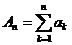 ;
;  ;
; 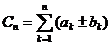 .
.
Отсюда видно, что между частными суммами рядов верно соотношение
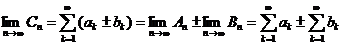 .
.
Признак сходимости Коши.
Пусть существует 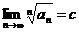 . Тогда
. Тогда
если с < 1, то ряд 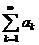 сходится;
сходится;
если с > 1, то ряд 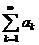 расходится;
расходится;
если с = 1, то вопрос о сходимости или расходимости ряда 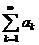 не может быть решен на основании данного признака.
не может быть решен на основании данного признака.
Этот признак сходимости носит название признака Коши.
Прежде, чем доказывать признак Коши рассмотрим ряд  , который называется геометрической прогрессией. Его частные суммы равны
, который называется геометрической прогрессией. Его частные суммы равны
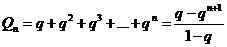 .
.
Рассмотрим теперь возможные варианты.
1. Пусть  . Тогда
. Тогда  и поэтому
и поэтому  и ряд
и ряд  сходится.
сходится.
2. Пусть 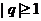 . Тогда общий член ряда
. Тогда общий член ряда  не стремится к нулю и, по признаку расходимости, ряд
не стремится к нулю и, по признаку расходимости, ряд  расходится.
расходится.
Таким образом, ряд  сходится при
сходится при  и расходится при
и расходится при 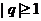 .
.
А теперь
Доказательство.
Прежде всего заметим, что существование 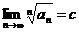 означает, что
означает, что
 .
.
А теперь - варианты.
1. Пусть 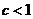 . Возьмем e настолько малым, чтобы было
. Возьмем e настолько малым, чтобы было 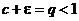 . Но тогда имеем
. Но тогда имеем
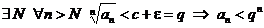 .
.
Но, так как 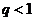 , ряд
, ряд  сходится, и, по теореме 2, сходится и ряд
сходится, и, по теореме 2, сходится и ряд 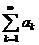 .
.
2. Пусть  . Возьмем e настолько малым, чтобы было
. Возьмем e настолько малым, чтобы было 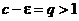 . Но тогда имеем
. Но тогда имеем
 .
.
Но, так как 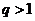 , ряд
, ряд  расходится, и, по теореме 2, расходится и ряд
расходится, и, по теореме 2, расходится и ряд 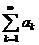 . <
. <
Теорема 3. Если "п выполнено условие  , тоиз сходимости ряда В следует сходимость ряда А, а из расходимости ряда А - расходимость ряда В.
, тоиз сходимости ряда В следует сходимость ряда А, а из расходимости ряда А - расходимость ряда В.
Доказательство.
Имеем следующую цепочку неравенств
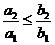 ;
;  ;
;  ; …
; … 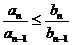 .
.
Перемножая эти неравенства, получаем
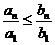 , или
, или  .
.
Ссылка на теорему 2 и доказывает эту теорему. <
Признак Даламбера
Пусть существует  . Тогда
. Тогда
если D < 1, то ряд 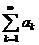 сходится;
сходится;
если D > 1, то ряд 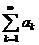 расходится;
расходится;
если D = 1, то вопрос о сходимости или расходимости ряда 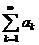 не может быть рншен на основании данного признака.
не может быть рншен на основании данного признака.
Доказательство.
Прежде всего заметим, что существование  означает, что
означает, что
 .
.
1. Пусть  . Возьмем e настолько малым, чтобы было
. Возьмем e настолько малым, чтобы было  . Но тогда имеем
. Но тогда имеем
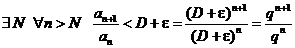 .
.
Но, так как 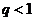 , ряд
, ряд  сходится, и, по теореме 3, сходится и ряд
сходится, и, по теореме 3, сходится и ряд 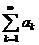 .
.
2. . Пусть  . Возьмем e настолько малым, чтобы было
. Возьмем e настолько малым, чтобы было 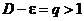 . Но тогда имеем
. Но тогда имеем
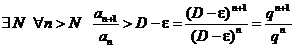 .
.
Но, так как 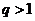 , ряд
, ряд  расходится, и, по теореме 3, расходится и ряд
расходится, и, по теореме 3, расходится и ряд 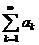 . <
. <
Теорема 4. Пусть существует 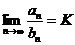 и
и 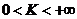 . Тогда ряды
. Тогда ряды 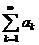 и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство.
1. Прежде всего отметим, что существование 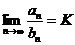 означает, что
означает, что
 .
.
2. Пусть ряд  сходится. Но тогда ряд
сходится. Но тогда ряд  также сходится, и, так как
также сходится, и, так как  , то, по теореме 2, сходится и ряд
, то, по теореме 2, сходится и ряд 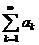 .
.
3. Так как 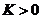 , то всегда можно взять e настолько малым, чтобы было
, то всегда можно взять e настолько малым, чтобы было  . Пусть теперь ряд
. Пусть теперь ряд 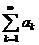 сходится. Но тогда сходится и ряд
сходится. Но тогда сходится и ряд 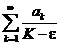 и, так как
и, так как  , то, по теореме 2, сходится и ряд
, то, по теореме 2, сходится и ряд  . <
. <
Гармонический ряд
Ряд
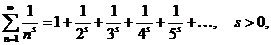
называется гармоническим рядом.
Теорема. Гармонический ряд сходится при  и расходится при
и расходится при  .
.
Доказательство.
Рассмотрим варианты.
1.  .
.
В этом случае гармонический ряд принимает вид
 .
.
Рассмотрим группу слагаемых следующего вида:
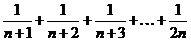 .
.
Очевидно, что в этой группе всего п слагаемых и самым маленьким является последнее слагаемое. Поэтому
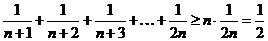 .
.
Теперь в ряде  сгруппируем слагаемые следующим образом
сгруппируем слагаемые следующим образом
 .
.
Группа  соответствует п = 2, группа
соответствует п = 2, группа 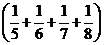 - п = 4 и т.д. Но тогда
- п = 4 и т.д. Но тогда
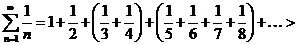

и поэтому 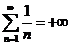 , то есть ряд
, то есть ряд  расходится.
расходится.
2.  .
.
Но в этом случае  ,
, 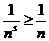 и поэтому
и поэтому 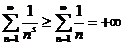 , то есть
, то есть  , и поэтому в этом случае ряд
, и поэтому в этом случае ряд 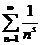 расходится.
расходится.
3.  .
.
В этом случае 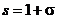 и
и  . Рассмотрим группу слагаемых вида
. Рассмотрим группу слагаемых вида
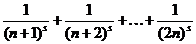 .
.
В этой группе п слагаемых и каждое из них меньше 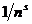 . Поэтому имеем
. Поэтому имеем
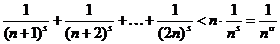 .
.
Теперь сгруппируем в гармоническом ряде слагаемые в группы
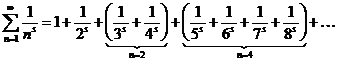 .
.
Группа  соответствует п = 2 и поэтому не превосходит
соответствует п = 2 и поэтому не превосходит 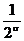 ; Группа
; Группа  соответствует п = 4 и поэтому не превосходит
соответствует п = 4 и поэтому не превосходит  ; последующая группа не превосходит
; последующая группа не превосходит 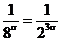 и т.д.
и т.д.
Окончательно получим
 .
.
Но стоящий в скобках ряд есть геометрическая прогрессия с  ; поэтому он сходится и, по теореме 2, сходится и ряд
; поэтому он сходится и, по теореме 2, сходится и ряд 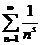 . <
. <
Следствие. Пусть существует  . Тогда при
. Тогда при  ряд
ряд  сходится, а при
сходится, а при  - расходится.
- расходится.
Доказательство. Рассмотрим ряд  с
с  . Тогда
. Тогда 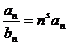 при выполнении условия
при выполнении условия  сходятся или расходятся одновременно (см. теорему 4). <
сходятся или расходятся одновременно (см. теорему 4). <
Заметим, что это не означает, что сходимость любого ряда можно выяснить с помощью этого признака. Например, для ряда 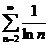
 при любом
при любом 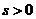 и следствие не работает.
и следствие не работает.
Интегральный признак Коши
Отсутствие универсального ряда для построения признака сходимости не означает, конечно, что не может быть других принципов для построения признаков сходимости числовых рядов. ниже будет разобран достаточно оригинальный признак сходимости, называемый интегральным признаком Коши.
Пусть функция 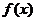
1. определена на промежутке  ;
;
2. монотонно убывает и  .
.
Рассмотрим ряд вида  , то есть слагаемые этого ряда имеют вид
, то есть слагаемые этого ряда имеют вид  .
.
Теорема. При указанных выше ограничениях ряд  сходится одновременно с несобственным интегралом
сходится одновременно с несобственным интегралом  .
.
Доказательство.
1. Основное неравенство.
Обозначим  . Так как
. Так как  , то
, то  . далее имеем
. далее имеем
 .
.
В силу монотонного убывания 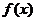
 ,
,
и поэтому в данном случае
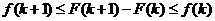 .
.
Это неравенство мы условно будем называть основным неравенством.
2. Пусть интеграл  сходится. Это значит, что
сходится. Это значит, что  . Но тогда имеем
. Но тогда имеем


 .
.
 | Переходя к пределу  , получаем, что , получаем, что  , откуда и следует, что ряд , откуда и следует, что ряд  сходится. Возникающая ситуация видна на прилагаемом рисунке: сумма площадей прямоугольников, каждый из которых равен одному слагаемому ряда, меньше площади, ограниченной функцией сходится. Возникающая ситуация видна на прилагаемом рисунке: сумма площадей прямоугольников, каждый из которых равен одному слагаемому ряда, меньше площади, ограниченной функцией 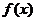 и осью абсцисс. и осью абсцисс. |
3. Пусть ряд  сходится.
сходится.
Тогда имеем
 ,
,
то есть  .
.
 | Переходя к пределу  , получаем, что , получаем, что  , откуда и следует, что интеграл , откуда и следует, что интеграл  сходится. Возникающая ситуация видна на прилагаемом рисунке: площадь, ограниченная функцией сходится. Возникающая ситуация видна на прилагаемом рисунке: площадь, ограниченная функцией 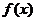 и осью абсцисс, меньше суммы площадей прямоугольников, каждый из которых равен одному слагаемому ряда. < и осью абсцисс, меньше суммы площадей прямоугольников, каждый из которых равен одному слагаемому ряда. < |
Знакопеременные ряды
Пусть имеется последовательность чисел 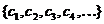 , такая, что
, такая, что 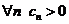 . Ряд
. Ряд
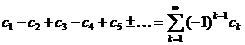
называется знакопеременным рядом.
Признак Лейбница. Если 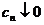 , то ряд
, то ряд 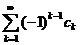 сходится.
сходится.
Доказательство.
Рассмотрим следующую частную сумму изучаемого ряда
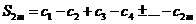
с чётныминдексом 2m. Ее можно записать двояко. Записывая ее в форме
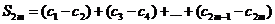
и вспоминая, что 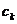 монотонно убывают,получаем,что все слагаемые положительны и поэтому
монотонно убывают,получаем,что все слагаемые положительны и поэтому 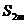 монотонно возрастают с ростом m. С другой стороны, записывая эту же частную сумму в виде
монотонно возрастают с ростом m. С другой стороны, записывая эту же частную сумму в виде
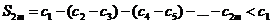 ,
,
так как все выражения, стоящие в скобках, опять-таки положительны. Поэтому, по теореме о пределе монотонно возрастающей последовательности, существует конечный 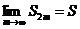 .
.
Рассмотрим теперь частные суммы знакопеременного ряда с нечетным индексом.Имеем
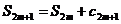 .
.
Но тогда
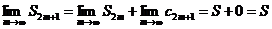 .
.
Поэтому вообще 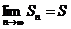 и ряд
и ряд 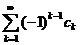 сходится. <
сходится. <
Признак Дирихле
Пусть
1. Все частные суммы ряда  ограничены, то есть
ограничены, то есть  ;
;
2.  .
.
Тогда ряд  сходится.
сходится.
Доказательство.
1. Согласно первому ограничению мы имеем

Пусть
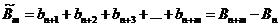 .
.
Тогда  .
.
2.  Þ
Þ  .
.
3. Считая, что 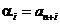 ,
,  , а также, что
, а также, что  и
и  используем преобразование Абеля. Получаем (вначале особых пояснений не требуется):
используем преобразование Абеля. Получаем (вначале особых пояснений не требуется):
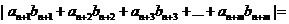 (делаем преобразование Абеля)
(делаем преобразование Абеля)


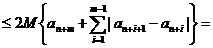
И тут наступает самый тонкий момент вывода. Вспомним, что, согласно ограничению 2, 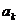 монотонно убывают. Поэтому все разности вида
монотонно убывают. Поэтому все разности вида  отрицательны,то есть
отрицательны,то есть  . В силу этого
. В силу этого
 ,
,
и, продолжая прерванный вывод, получим:
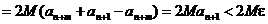 .
.
Но e сколь угодно мало. Поэтому, со ссылкой на признак сходимости Больцано-Коши, можно утверждать, что ряд  сходится. <
сходится. <
Следствие. Если  ,то сходятся ряды
,то сходятся ряды 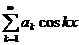 (при
(при 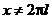 ) и
) и 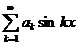 (при любых х).
(при любых х).
Доказательство.
Пусть  . Начнем с известной со школы формулы
. Начнем с известной со школы формулы
 .
.
Имеем
k = 1: 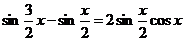 ;
;
k = 2: 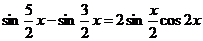 ;
;
k = 3:  ;
;
……………..
k = n: 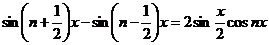 .
.
Складывая все эти равенства, получим:
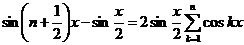 .
.
Теперь мы имеем очень интересную формулу
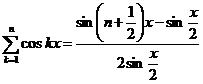 .
.
Но тогда
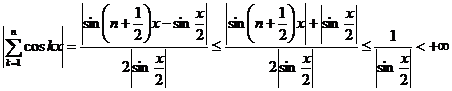 ,
,
если 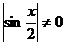 , то есть, если
, то есть, если 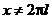 . По признаку Дирихле, при
. По признаку Дирихле, при 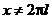 ряд
ряд 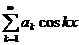 сходится.
сходится.
Для ряда 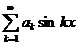 все выкладки совершенно аналогичны, надо только начинать с формулы
все выкладки совершенно аналогичны, надо только начинать с формулы
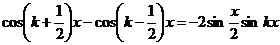 .
.
Условие 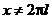 можно убрать, так как при
можно убрать, так как при 
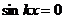 и сумма ряда просто равна нулю.
и сумма ряда просто равна нулю.
Признак Абеля. Если ряд  сходится (не обязательно абсолютно!), а последовательность чисел
сходится (не обязательно абсолютно!), а последовательность чисел 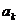 монотонна и ограничена, то ряд
монотонна и ограничена, то ряд  сходится.
сходится.
Доказательство.
1. Ряд  сходится Þ по признаку Больцано-Коши
сходится Þ по признаку Больцано-Коши
 .
.
2. Последовательность чисел 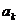 ограничена Þ
ограничена Þ 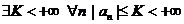 .
.
3. Дальнейшие выкладки сначала полностью повторяют признак Больцано-Коши
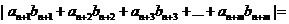 (делаем преобразование Абеля)
(делаем преобразование Абеля)


С этого момента начинаются отличия. Если раньше действовала оценка  , то теперь будет оценка
, то теперь будет оценка 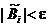 :
:

В этом месте - самый тонкий момент. Согласно ограничению, последовательность чисел 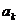 монотонна Þ все разности
монотонна Þ все разности 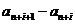 одного знака, или все положительные, или все отрицательные. Поэтому можно записать
одного знака, или все положительные, или все отрицательные. Поэтому можно записать
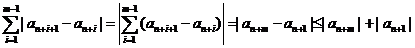 .
.
Поэтому, продолжая доказательство, можно записать:
 .
.
Заключительная фраза та же самая: e сколь угодно мало. Поэтому, со ссылкой на признак сходимости Больцано-Коши, можно утверждать, что ряд  сходится. <
сходится. <
Перемножение рядов
Пусть даны два ряда
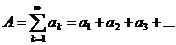 (ряд А) и
(ряд А) и
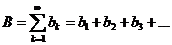 (ряд В).
(ряд В).
Как определить произведение этих рядов?
Рассмотрим бесконечную матрицу
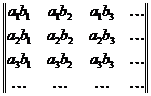 ,
,
составленную из всевозможных произведений вида 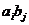 . Нам надо сложить все элементы этой матрицы. Как это сделать? Моно, например, по диагоналям складывать
. Нам надо сложить все элементы этой матрицы. Как это сделать? Моно, например, по диагоналям складывать
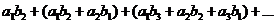 , (*)
, (*)
а можно и так
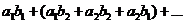 ,
,
можно еще тысячами разных способов. Но где гарантия, что все эти ряды имеют одну и ту же сумму?
Теорема Коши. Если ряды (А) и (В) сходятся абсолютно, то их произведение, составленное из слагаемых вида 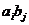 , взятых в любом порядке, также сходится и имеет своей суммой
, взятых в любом порядке, также сходится и имеет своей суммой 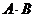 .
.
Доказательство.
Рассмотрим ряд вида
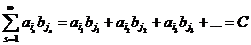
в которое входят все комбинации типа 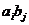 , и рассмотрим его частную сумму
, и рассмотрим его частную сумму
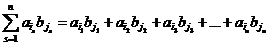 .
.
Пусть 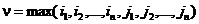 . Тогда
. Тогда
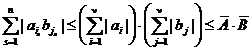 ,
,
где 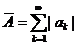 ,
, 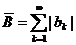 . Следовательно, ряд
. Следовательно, ряд 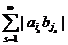 сходится. В силу этого ряд
сходится. В силу этого ряд 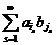 сходится абсолютно и поэтому его слагаемые можно располагать в любом порядке. Беря частные суммы ряда С в виде
сходится абсолютно и поэтому его слагаемые можно располагать в любом порядке. Беря частные суммы ряда С в виде
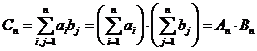
и поэтому 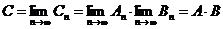 . <
. <
на практике чаще всего суммируют по диагоналям бесконечной матрицы, как в (*).
Двойные ряды
Обобщением рассмотренной выше ситуации является следующая. Дана бесконечная матрица
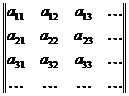 .
.
Рассмотрим суммы 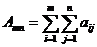 . Рассмотрим двойной предел, когда m и n одновременно независимо друг от друга стремятся в + ¥ (более строгое определение понятия двойного предела смотрите в следующей главе):
. Рассмотрим двойной предел, когда m и n одновременно независимо друг от друга стремятся в + ¥ (более строгое определение понятия двойного предела смотрите в следующей главе):
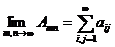 ,
,
который называется двойным рядом, и обозначается символом 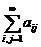 .
.
Кроме этого можно рассмотреть и так называемые повторные пределы, когда в + ¥ уходит сначала n, а потом т
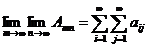 ,
,
или, наоборот, сначала т, а потом п
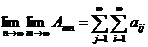 .
.
Они называются повторными рядами.
Теорема. Если из трех рядов
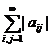 ,
, 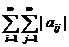 ,
, 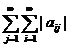
то сходятся и два остальные и верно равенство
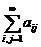 =
= 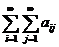 =
= 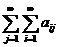 .
.
Доказательство.
1. Пусть 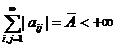 . Тогда очевидно, что
. Тогда очевидно, что 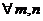
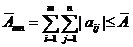 . Но
. Но 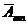 монотонно возрастает с ростом п, и, в силу ограниченности сверху, существует конечный предел
монотонно возрастает с ростом п, и, в силу ограниченности сверху, существует конечный предел 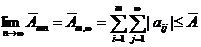 .
.
Но 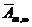 также монотонно возрастает с ростом т, и также ограничена сверху. Поэтому существует и повторный предел
также монотонно возрастает с ростом т, и также ограничена сверху. Поэтому существует и повторный предел
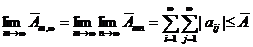
и ряд 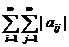 сходится. Совершенно аналогично показывается сходимость ряда
сходится. Совершенно аналогично показывается сходимость ряда 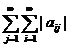 .
.
2. Пусть теперь 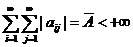 . Тогда
. Тогда 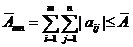 . Но
. Но 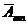 монотонно возрастают с ростом п и т, и, в силу ограниченности
монотонно возрастают с ростом п и т, и, в силу ограниченности 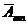 сверху, существует двойной предел
сверху, существует двойной предел 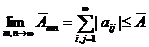 .
.
3. Сравнивая полученные неравенства легко получить, что суммы всех этих трех рядов равны между собой
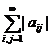 =
= 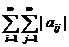 =
= 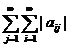 .
.
Но тогда ряды
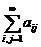 ,
, 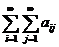 ,
, 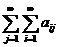 .
.
Сходятся абсолютно, и, в силу этого, в них можно произвольно переставлять слагаемые, их суммы от этого не изменятся. Поэтому
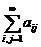 =
= 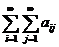 =
= 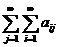 . <
. <
Бесконечные произведения
В заключение этой главы рассмотрим коротко достаточно экзотический раздел математического анализа - так называемые бесконечные произведения.
Определения.
Пусть имеем последовательность вещественных чисел 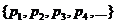 , которые все отличны от нуля.Рассмотрим так называемые частные произведения
, которые все отличны от нуля.Рассмотрим так называемые частные произведения
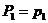 ;
; 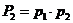 ;
; 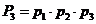 ; …
; … 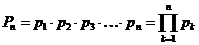 .
.
Предел 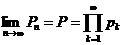 называется бесконечным произведением. Если этот предел существует, конечен и отличен от нуля, то говорят, что бесконечное произведение сходится, в противном случае - расходится.
называется бесконечным произведением. Если этот предел существует, конечен и отличен от нуля, то говорят, что бесконечное произведение сходится, в противном случае - расходится.
Величина 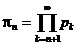 называется остаточным произведением после п-го сомножителя.
называется остаточным произведением после п-го сомножителя.
Свойства
1. Если бесконечное произведение сходится, то " п сходится и остаточное произведение. Наоборот, если какое-то остаточное произведение сходится, то сходится и само бесконечное произведение и верна формула
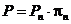
Доказательство.
А) Пусть существует 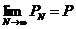 . Но тогда
. Но тогда 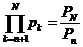 и, делая предельный переход N ® ¥, получим
и, делая предельный переход N ® ¥, получим
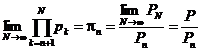 .
.
Б) Пусть существует 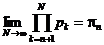 . Но тогда
. Но тогда 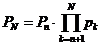 и поэтому
и поэтому 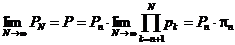 .
.
2. Если бесконечное произведение сходится, то 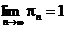 .
.
Действительно, 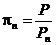 и поэтому
и поэтому 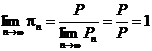 .
.
3. Если бесконечное произведение сходится, то 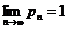 .
.
Действительно, 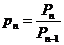 и поэтому
и поэтому 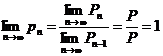 .
.
Следствие. Если бесконечное произведение сходится, то, начиная с некоторого N, все 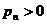 .
.
Этими простейшими свойствами мы ограничимся.
Признаки сходимости
Теорема 1. для того, чтобы бесконечное произведение сходилось необходимо и достаточно, чтобы сходился ряд 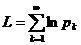 .
.
Доказательство.
Имеем
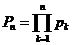 ;
; 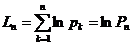 ;
; 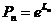 .
.
Используя непрерывность логарифмической и показательной функций, получаем:
А) 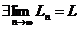 Þ
Þ 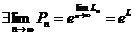 .
.
Б) 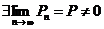 Þ
Þ 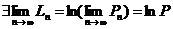 . <
. <
Так как 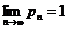 , то представим
, то представим 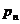 в виде
в виде 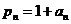 . Тогда
. Тогда 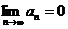 .
.
Теорема 2. Пусть, начиная с некоторого N, все 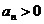 . Тогда, для сходимости бесконечного произведения необходимо и достаточно, чтобы сходился ряд
. Тогда, для сходимости бесконечного произведения необходимо и достаточно, чтобы сходился ряд 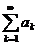 .
.
Доказательство.
Так как 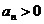 ,то
,то 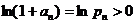 . Далее, так как
. Далее, так как 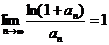 , то ряды
, то ряды 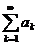 и
и 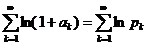 сходятся или расходятся одновременно. <
сходятся или расходятся одновременно. <
Теорема 3. Из сходимости рядов 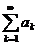 и
и 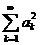 следует сходимость бесконечного произведения.
следует сходимость бесконечного произведения.
Доказательство.
Примем без доказательства неравенство 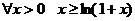 . Можете попытаться доказать его сами.
. Можете попытаться доказать его сами.
Далее, применяя правило Лопиталя, легко получить, что
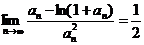 .
.
Далее идет следующая цепочка следований:
Ряд 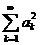 сходится Þ ряд
сходится Þ ряд 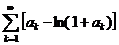 также сходится. Но так как сходится ряд
также сходится. Но так как сходится ряд 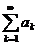 , то сходится и ряд
, то сходится и ряд 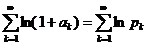 Þ бесконечное произведение сходится. <
Þ бесконечное произведение сходится. <
Еще кое-что
Бесконечное произведение 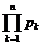 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если 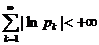 . Если ряд
. Если ряд 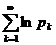 сходится, но
сходится, но 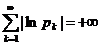 , то бесконечное произведение
, то бесконечное произведение 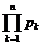 называется неабсолютно сходящимся
называется неабсолютно сходящимся
В абсолютно сходящемся произведении можно как угодно переставлять сомножители - от этого оно не изменится. В неабсолютно сходящемся произведении перестановка сомножителей может изменить значение бесконечного произведения.
Глава 9. Числовые ряды
Определения
Пусть дана последовательность вещественных чисел 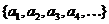 . Образуем новую последовательность по правилу
. Образуем новую последовательность по правилу
