Множества считаются равными тогда и только тогда, когда

Множества

Множества и элементы

Под множеством понимают произвольное собрание различных предметов. Предметы, входящие в это собрание, называются элементами этого множества. Множество состоит из своих элементов. Оно образовано из них.

То, что x является элементом множества A, обозначается формулой

x ∈ A.

При этом говорят, что x принадлежит множеству A и A содержит x.

Значок ∈ называется символом принадлежности.

Формулу x ∈ A записывают и так: A ∋ x. Этим подчёркивается очевидная аналогия с

символами 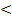и .

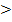Тот факт, что x не является элементом множества A, записывается формулой

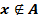или .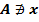

Равенство множеств

Множество определяется своими элементами. Оно есть не что иное, как собрание своих элементов. Наиболее выпукло это проявляется в следующем:

Множества считаются равными тогда и только тогда, когда

Они состоят из одних и тех же элементов.

В этом смысле слово “множество” имеет слегка уничижительный оттенок: когда мы говорим множество, мы подчёркиваем своё сиюминутное равнодушие к какой бы то ни было организации его элементов.

Например, говоря, что прямая есть множество точек, мы даём основание предположить, что две прямые совпадают тогда и только тогда, когда они состоят из одних и тех же точек. С другой стороны, мы обязуемся все взаимоотношения точек (расстояния между ними, их порядок на прямой и т. п.) рассматривать отдельно, не включая их в понятие прямой.

Элементы, в свою очередь, могут быть множествами, но постольку, поскольку они рассматриваются как элементы, они исполняют роль своего рода атомов, чья внутренняя жизнь игнорируется.

Множество можно представлять себе как воображаемый ящик, предназначенный для того, чтобы отделить элементы этого множества от прочих вещей. Соединение каких-то вещей в множество даёт возможность присвоить им общее имя и демонстрирует намерение рассматривать эти вещи как единую общность, не вдаваясь до поры до времени в их природу и отношения между собой.

Пустое множество

Итак, элемент не может быть без множества. А вот множество может быть без единого элемента. Имеется всего одно такое множество (поскольку множество определяется запасом своих элементов). Оно называется пустым и обозначается символом ∅.

Основные числовые множества

Наряду с ∅ имеются и другие уникальные множества, столь важные, что они получили свои собственные общепринятые названия и обозначения.

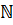- множество всех натуральных чисел, т. е. 1, 2, 3, 4, 5,…

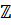- множество всех целых чисел (как положительных целых, т. е. натуральных чисел, так и отрицательных и нуля).

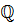- множество всех рациональных чисел (добавьте к целым числам числа, представимые дробями, т. е. такие, как, например, , ).

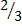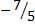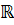- множество всех вещественных чисел (полученное присоединением к множеству 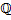иррациональных чисел таких, как, например, 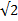и π = 3.14…).

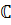- множество комплексных чисел.

Задание множества явным перечнем его элементов

Множество, заданное списком a, b,…, x своих элементов, обозначается символом

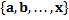
Другими словами, список объектов, заключенный в фигурные скобки, обозначает множество, элементы которого перечислены в этом списке.

Например, {1, 2, 123} – множество, состоящее из чисел 1, 2 и 123.

Формула {a, x,A} обозначает множество, состоящее из элементов a, x и A, какие бы объекты эти три буквы ни обозначали.

Примеры.

1. Что такое {∅}? Сколько элементов в этом множестве?

Множество {∅} состоит из одного элемента, каковым является пустое множество ∅. Конечно, сам этот элемент есть пустое множество, которое не содержит элементов, но множество {∅} состоит из единственного элемента ∅.

2. Нижеследующие формулы верны:

1)

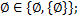
2)

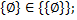
3) .

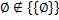Множество, состоящее из одного элемента, так и называется одноэлементным.

3. Является ли множество {{∅}} одноэлементным?

Да, множество {{∅}} состоит из одного элемента, его единственным элементом является множество {∅}.

Заметьте, что множества {1, 2, 3} и {3, 2, 1, 2} равны, поскольку они состоят из одних и тех же элементов. На первый взгляд, список с повторениями никогда не может возникнуть естественным образом. Появляется даже соблазн на всякий случай запретить списки с повторениями в подобных обозначениях. Однако, в данном случае запрет этот не был бы разумным. Действительно, часто никто не может сказать, имеются в списке повторения или нет. Например, если элементы списка зависят от параметра, то при одних значениях параметра некоторые члены списка могут совпасть, тогда как при других значениях они окажутся различными.

4. Сколько элементов содержат следующие множества?

1) {1, 2, 1} – 2 элемента;

2) 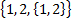– 3 элемента;

3) 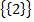– 1 элемент;

4) 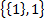– 2 элемента;

5) 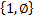– 2 элемента;

6) 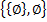– 2 элемента;

7) 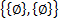– 1 элемент;

8) 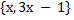при 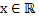– два элемента, если 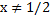, и один элемент, если ;

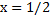Подмножества

Если каждый элемент множества A принадлежит и множеству B, то говорят, что A есть подмножество множества B и что B содержит множество A, а также пишут

A ⊂ B и B ⊃ A.

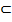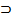Знаки и называются символами включения.

Не случайно они напоминают знаки неравенства 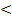и :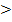

Утверждение.

Пусть множество A состоит из a элементов, а множество B - из b элементов. Если A ⊂ B, то a < b.

Доказательство.

Что значит, что A состоит из a элементов? Это значит, что мы можем пересчитать элементы множества A, присваивая им номера 1, 2, 3, и т. д. и что последний элемент при этом получит номер a. Известно, что результат не зависит от порядка, в котором мы расположили элементы множества. (В действительности, можно развить теорию множеств, которая включала бы теорию счёта, где это доказывалось бы как одна из основных теорем. Но поскольку это не вызывает сомнений, мы опускаем доказательство.) Поэтому мы можем начать подсчёт элементов множества B с подсчёта элементов множества A. Пересчитав элементы множества A, мы продолжим подсчёт, если какие-то элементы множества B к этому моменту останутся не сосчитанными. Поэтому число элементов множества A не превосходит числа элементов множества B.

Пример.

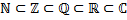
Свойства включения

I. Рефлексивность включения.

A ⊂ A для любого множества A,

Включение и принадлежность

I.

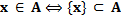
Доказательство.

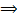
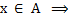по опр. включения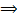

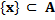
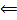
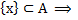любой элемент множества 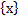является и элементом множества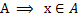

Замечание.

Несмотря на эту очевидную связь и похожесть символов принадлежности ∈ и включения ⊂, понятия принадлежности и включения весьма различны:

принадлежность A ∈ B означает что A - один из элементов множества B

(т. е. один из неделимых объектов, составляющих B),

включение A⊂B означает, что A состоит из некоторых элементов множества B.

II. Нерефлексивность принадлежности.

Существует такое множество A, что .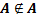

Доказательство.

Построить такое множество A, что A 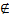A, легко. Возьмите, например, A = ∅, или A = N, или A = {1},…

III. . Нетранзитивность принадлежности.

Существуют такие множества A, B и C, что A ∈ B и B ∈ C, но .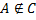

Доказательство.

Пусть 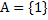, 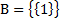и 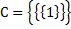. Ясно, что A ∈ B и B ∈ C, но .

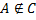На самом деле, труднее построить такие множества A, B и C, что A ∈ B, B ∈ C и A ∈ C. Вот один из простейших примеров: , ,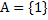

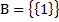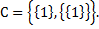
1.10. Задание подмножества заданием условия

Как мы знаем (см. п. 1.5), множество можно описать, представив список его элементов. К сожалению, этот простейший способ задания множеств не всегда доступен и уж во всяком случае не всегда лёгок. Например, легко сказать: “множество всех решений следующего уравнения” и выписать уравнение. Это - вполне приемлемое недвусмысленное описание множества. Приняв его, можно говорить об этом множестве, обсуждать его свойства, и, в результате, если повезёт, решить уравнение и выписать список всех его решений.

(Последнее может оказаться не лёгким делом, но тот факт, что мы не имеем списка всех решений уравнения, не должен помешать нам рассуждать о множестве всех его решений.)

Итак, множество можно задать, сформулировав свойства, выделяющие его элементы среди элементов более широкого и уже описанного множества. Соответствующее обозначение: подмножество множества A, состоящее из элементов x, которые удовлетворяют условию P(x), обозначается через

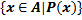или .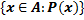

Примеры.

Зададим следующие множества списками их элементов (т. е. в виде {a, b,…}):

1) {x ∈ 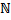| x < 5} = {1, 2, 3, 4};

2) {x ∈ 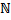| x < 0} = { };

3) {x ∈ 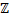| x < 0} = {−1,−2,−3,−4,−5,−6, . . .}.

Пересечение и объединение

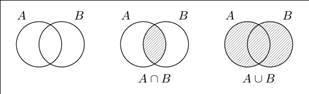
Пересечением множеств A и B называется множество, составленное из их общих элементов, т. е. элементов, принадлежащих и A, и B. Оно обозначается через A∩B. Его можно описать и формулой

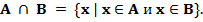
Множества A и B называются дизъюнктными или непересекающимися, если их пересечение пусто, т. е. A ∩ B = ∅.

Объединением множеств A и B называется множество, составленное из элементов, каждый из которых принадлежит хотя бы одному из множеств A и B.

Объединение множеств A и B обозначается через A ∪ B. Его можно описать формулой

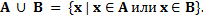
Здесь союз и л и понимается в неисключающем смысле: условие “x∈A или x∈ B” означает, что x принадлежит х о т я б ы о д н о м у из множеств A и B, а, быть может, и обоим.

Примеры.

1) ;

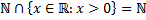2) ;

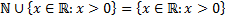3) ;

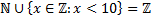I. Коммутативность

Для любых множеств A и B выполнены равенства

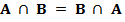
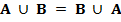
II. Ассоциативность

Для любых множеств A, B и C выполнены равенства

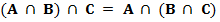
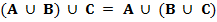
Разные разности

Разностью 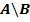множеств A и B называется совокупность тех элементов множества A, которые не принадлежат множеству B.

При этом, вообще говоря, не предполагается, что .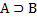

В случае, если 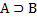, множество 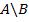называется также дополнением множества B в множестве A.

Свойства операции разности

I. Для любых множеств A и B

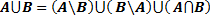
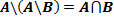
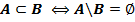
II. Для любых множеств A, B и C

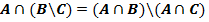
Симметрической разностью множеств A и B называется множество

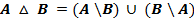
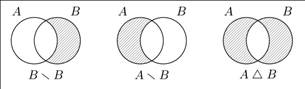
Формулы де Моргана

Пусть 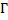– произвольная совокупность подмножеств множества .

Тогда

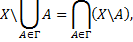
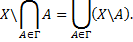
Доказательство.

1 часть.

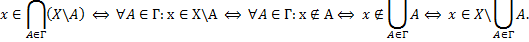
2 часть.

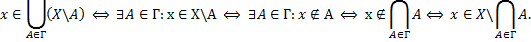
Промежутки

Пусть .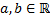

Отрезком (замкнутым промежутком) с концам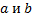и при 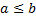называется множество

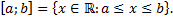
Интервалом(открытым промежутком)с концам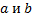и при 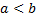называется множество

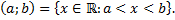
Полуоткрытыми промежуткамис концами 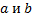называют множества

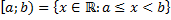
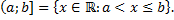
Замечание.

Если нам безразлично включаются ли концы в промежуток (произвольный промежуток), то будем употреблять угловые скобки .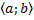

Лучами с концом 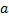будем называть следующие множества

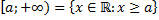
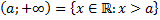
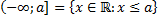
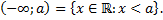
К промежуткам также будем относить числовую прямую

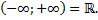
Отображения и функции

Отображения и функции

Определение.

Пусть 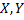– некоторые множества, а 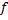– правило, сопоставляющее каждому элементу 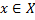единственный элемент 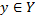, обозначаемый через 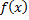, то есть :

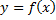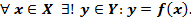
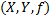– упорядоченная тройка – отображениемножества в множество .

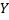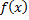– образ элемента 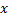при этом отображении;

– значение отображения на элементе .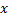

Множество – область (множество) задания отображения.

Множество 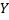– множество прибытия.

Замечание.

Иногда словом “отображение” называют только правило 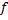, но при этом всегда подразумеваются указания множеств .

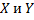В зависимости от множеств 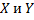отображение может обладать разными свойствами.

Пример.

Сравнить свойства следующих отображений:

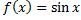
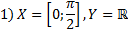
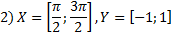
Обозначение отображения.

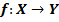
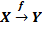
Замечание.

Синонимы термина “отображение”: оператор, операция, преобразование.

Иногда элементы называют независимой переменной, имея в виду, что элементы множества 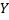меняются в зависимости от . (Понятие отображения выражает интуитивное представление о том, как одна величина полностью определяет значение другой.)

Функции

Функцией будем называть отображение в множество 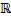, т.е. .

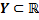Комплексная (комплекснозначная)функция– отображение в множество 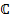, т.е. .

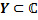Образ и прообраз

Определение прообраза.

Определение.

Пусть 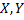– некоторые множества, , .

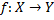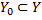Прообразом множества 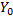при отображении 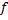называется множество

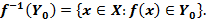
Определение образа.

Определение.

Пусть 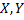– некоторые множества, , .

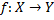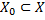Образом множества 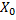при отображении 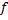называется множество всех тех 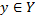, для которых существует 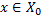, такое что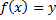

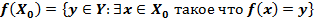
Замечание №1.

Не обязательно, образ всего множества совпадает со всем множеством .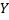

Мощность множества

Определение.

Пусть 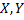– произвольные множества, говорят, что множества 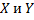имеют одинаковую мощность (являются равномощными), если существует биекция множества на множество .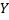

Замечание.

Конечные множества равномощны тогда и только тогда, когда имеют одинаковое число элементов.

Замечание.

Бывают неравномощные бесконечные множества. К примеру, множество 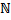неравномощно множеству .

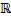Определение.

Множество, равномощное множеству 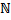, называют счётным.

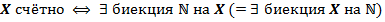
Определение.

Множество – не более чем счётное, если – конечно или счётно.

Теорема.

Множество 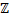счётно.

Доказательство.

Теорема.

Бесконечное подмножество счётного множества счётно.

Доказательство.

Замечание.

Любые 2 счётных множества равномощны.

Доказательство.

Теорема.

Прямое (декартово) произведение счётных множеств счётно.

Теорема.

Множество всех рациональных чисел 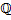счётно.

Композиция отображений

Определение.

Пусть 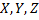– некоторые множества.

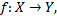
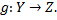
Композицией отображени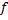й и 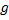называется отображение

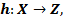
такое что

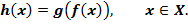
Обозначение композиции

Композиция отображени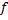й и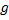

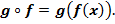
Замечание №1.

Выражение 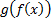имеет смысл, т.к. .

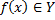Замечание №2.

Переставлять 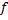и 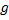местами вообще говоря нельзя.

Пример.

Пусть

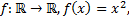
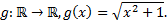
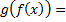
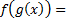
Замечание №3.

Аналогично можно определить композицию не 2-х, а 3-х и более отображений.

Придумайте примеры.

Обратное отображение

Пусть 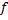– биекция множества на множество .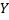

Рассмотрим отображение 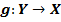, которое каждому 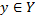сопоставляет 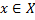, такое что 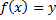, т.е.

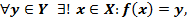
(существование и единственность такого элемента 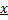следует из определения биекции)

Такое отображение 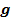называется обратными обозначается символом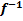

(т.е. )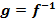

Примеры.

I. Пусть .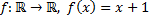

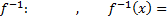
II. Пусть .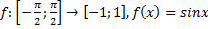

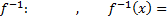
Замечание.

Пусть 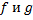– отображения

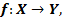
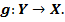
Тогда

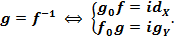
Функции и действия над ними

Сумма функций.

Определение.

Пусть 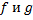– функции

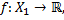
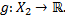
Суммой функций 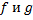называется функция

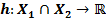
такая что

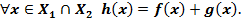
Пример.

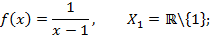
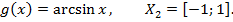
Тогда

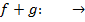
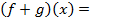
Разность функций.

Определение.

Пусть 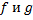– функции

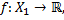
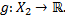
Разностью функций 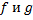называется функция

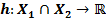
такая что

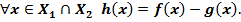
Произведение функций.

Определение.

Пусть 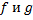– функции

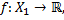
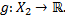
Произведением функций 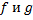называется функция

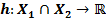
такая что

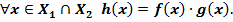
Частное функций.

Определение.

Пусть 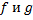– функции

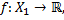
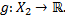
Пусть

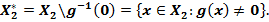
Частным функций 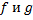называется функция

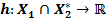
такая что

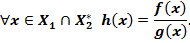
Степень функции.

Замечание.

Используя определения произведения и частного можем определить натуральную и целую степени функции.

Определение.

Пусть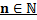

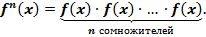
Пусть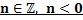

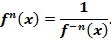
(функция 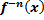определена, т.к. .)

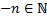Замечание.

Нельзя путать

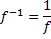
с обратным отображением и обозначением прообраза.

Окрестность точки.

Определение.

Пусть 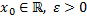. 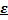- окрестностью точки 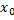называют множество

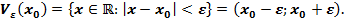
Проколотой 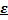- окрестностью точки 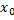называют множество

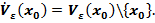
Если в течении достаточно большого промежутка времени фиксировано множество , в котором рассматриваются точки 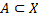, дополнением множества (до пространства ) называют множество

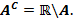
Часть.

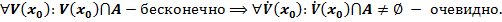
Часть.

.

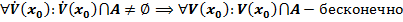Предположим от противного:

Пусть для 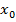выполнено условие: 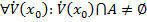, и при этом существует окрестность точки 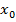, пересекающаяся с множеством 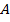по конечному множеству точек, т.е.

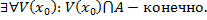
Занумеруем точки пересечения:

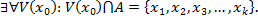
Выберем минимальное из расстояний между точкой 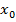и точками 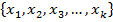, т.е.

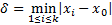
Тогда

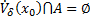
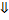
Получаем противоречие.

Замечания.

I. Изолированная точка множества не просто принадлежит множеству , но и является его граничной точкой.

II. Точки сгущения – предельные точки множества.

III. Точка сгущения может как принадлежать множеству , так и не принадлежать ему.

IV. Внешняя точка множества не может быть точкой сгущения.

V. Изолированная точка множества не может быть точкой сгущения.

Привести примеры к замечаниям.

Обозначение.

Множество всех предельных точек множества (всех его точек сгущения) называют производным множеством множества и обозначают

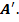
Задача.

Заполнить таблицу.

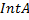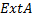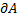				Изолированные точки

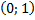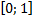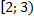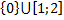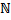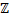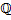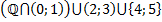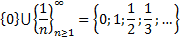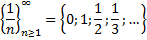Открытые множества

Определение.

Множество 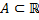называется открытым, если каждая его точка – внутренняя точка множества .

Замечание.

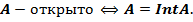
Теорема.

Открытое множество на прямой – объединение некоторого семейства лучей и интервалов.

Свойства открытых множеств.

Теорема 1.

Объединение любого семейства открытых множеств открыто.

Доказательство.

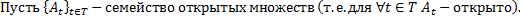
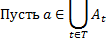
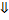
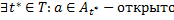
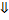
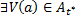
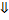
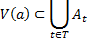
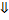
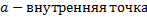
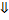
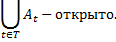
Замечание.

Пересечение любого семейства открытых множеств не обязано быть открытым.

Приведите пример.

Теорема 2.

Пересечение конечного числа открытых множеств открыто.

Доказательство.

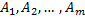– открытые множества.

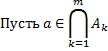
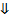
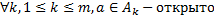
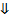
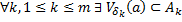
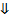
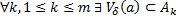
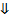
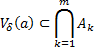
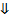
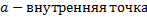
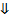
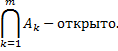
Замкнутые множества

Определение.

Множество 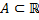называется замкнутым,

n если оно содержит все свои конечные точки сгущения, т.е. .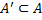

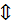
n если его дополнение открыто.

Доказательство равносильности.

1 часть. .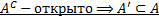

Предположим от противного:

Пусть 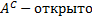, при этом существует хотя бы ода предельная точка, не содержащаяся в :

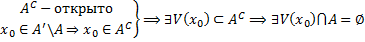
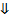
То есть, в окрестности 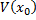нет ни одной точки множества .