Методика виконання завдання.

Луцьк 2014

УДК 515.2

ББК

Методичні вказівки до самостійної роботи для студентів напряму підготовки 0505 „Машинобудування” скороченого терміну денної та заочної форм навчання з дисципліни „Нарисна геометрія, інженерна та комп’ютерна графіка”. / Бурчак І. Н., Клак Ю.В. - Луцьк: РВВ ЛуцькогоНТУ, 2014.- 28 c.

Укладачі: к.т.н. доц.. Бурчак І.Н., ас. Клак Ю.В.

Рецензент: к.т.н. доц. Головачук І.П.

Відповідальний за випуск: к.т.н. доц. Головачук І.П.

Затверджено науково-методичною радою ЛДТУ,

Протокол № від 2014 р.

Рекомендовано до друку науково-методичною радою інституту НВІ ІІТ ЛДТУ,

Протокол № від 19.12 2014 р.

Розглянуто на засіданні методичного семінару кафедри інженерної

та комп’ютерної графіки.

Протокол № 7 від 11.12 2014 р.

ã І. Н. Бурчак, Ю.В.Клак 2014

Вступ

Розроблені методичні вказівки регламентують виконання самостійних робіт для студентів спеціальності Мс денної та заочної форм навчання та відповідають типовій робочій програмі – “Нарисна геометрія, інженерна та комп’ютерна графіка”, рекомендованої науково-методичним центром вищої освіти Міністерства освіти і науки України для студентів технічних спеціальностей вищих навчальних закладів України (К.: НАУКОВО-МЕТОДИЧНИЙ ЦЕНТР ВИЩОЇ ОСВІТИ, 2005).

Анотація. Комп'ютерною, або машинною, графікою називають наукову дисципліну, яка розробляє сукупність засобів та прийомів автоматизації кодування, обробки й декодування графічної інформації.

Геометричне моделювання має своєю метою опис об’єктів, предметів та явищ, що відзначаються геометричними властивостями, тому найбільш придатнім для них є графічне представлення.

Важливим розділом двовимірного та тривимірного моделювання є формування об’єкта засобами комп’ютерної графіки (КГ). Перш за все КГ ефективна при автоматизації трудомістких креслярських та конструкторських робіт. Комп’ютерна графіка успішно використовується також при виконанні робочих креслеників об’єктів машино- та приладобудування, будівництва та архітектури.

Комп’ютерна графіка, нарешті, широко впроваджується в сучасне мистецтво, дизайн та рекламу, особливо, якщо взяти до уваги, що зараз можна одержувати високоякісні зображення в різних проекційних системах з використанням кольору, світлотіні і, навіть, фактури поверхні.

Мета курсу – засвоєння теоретичних основ побудови растрових та векторних зображень, опанування студентами методів побудови зображень просторових форм, вміння користуватися CAD – системами, пов’язаних із просторових формами, набуття навичок складання раціональної послідовності розв’язання задач геометричного моделювання, вивчення методів побудови 2D та 3D зображень простих предметів.

Відповідно до навчального плану передбачаються лекції та лабораторні заняття. Згідно робочої програми студенти виконують чотири лабораторні роботи на виконання яких відведено на стаціонарі 18 годин, на заочній формі – 4 години.

Попередньо варто ознайомитися з програмою дисципліни, переліком питань, які винесені на підсумковий контроль, літературою.

Значна роль відведена конспекту при вивченні такого розділу, як комп’ютерна графіка, тому що конспектування привчає студента самостійно мислити і коротко формулювати основні положення курсу.

1. Графічні роботи

Студенти оформляють графічні роботи, які є результатом виконання лабораторних робіт і являють собою набір задач, виконаних на креслярському папері, а також “тверді” копії комп’ютерних зображень, виконаних за індивідуальним варіантом і оформлених відповідно до викладених вимог.

Варіант завдання на графічні та комп’ютерні роботи видається студенту на заняттях індивідуально. Правильність виконання студентом графічних робіт свідчить про засвоєння основних положень курсу і оволодіння технікою роботи з комп’ютером.

Студентам заочної форми навчання графічні роботи варто подавати для рецензії дотримуючись термінів, передбачених навчальним графіком. Кресленики графічних робіт виконуються на форматі А3(297х420мм), викреслюється титульний лист, скріпляється і подається для рецензування поштою або представляється особисто. На перевірку варто представляти графічні роботи тільки в повному обсязі (некомплектні роботи та роботи без електронних носіїв інформації повертаються студенту без перевірки).

Титульний лист

Титульний лист графічних робіт оформляється відповідно до ГОСТ 2.304-81. Зразок виконання титульного листа наведений на рис. 1. При перевірці графічних робіт студентів заочної форми навчання викладач кафедри складає рецензію на титульному листі, у якій коротко відзначає недоліки, а також дає остаточну оцінку: допущена чи не допущена робота до захисту. Робота допускається до захисту, якщо вона заслуговує позитивної оцінки. Якщо графічні роботи допущені до захисту, але містять зауваження, що вимагають внесення виправлень, то ці виправлення повинні бути внесені до моменту захисту робіт. Якщо графічніроботи не допущені до захисту, тобто оцінені оцінкою “незадовільно”, вони повинні бути виправлені, перероблені повністю або частково, відповідно до зауважень викладача і представлені на повторну рецензію.

На повторну рецензію варто висилати також і раніше підписані листи, що входять у роботу, разом із попередньою рецензією, а також комп’ютерні файли на носіях електронної інформації.

Захист графічних робіт є співбесідою викладача зі студентом по виконаних листах та перевіркою комп’ютерної інформації. При захисті з’ясовується хід рішення окремих задач, порядок виконання, обґрунтуванняспособу рішення, практичні навички роботи в комп’ютерних програмах. Захист графічних робіт проводиться після їх перевірки й одержанняна них позитивної рецензії (допущені до захисту) у час консультацій викладача протягом семестру в спеціально відведені години або в період сесії. Студент, що не захистив графічних робіт, до диференційованого заліку

не допускається.

Метою захисту графічних робіт є не лише перевірка на самостійність їх виконання, але й розвиток творчості студента, просторової уяви і логічного мислення, тобто є продовженням навчального процесу.

Рис.1

3. Вимоги до оформлення

самостійних та індивідуальних робіт

Графічні роботи повинні бути виконані згідно зі стандартами Єдиної системи конструкторської докумен-тації і вирізнятися виразністю, акуратністю і чіткістю графічного виконання. Якість графічного виконання креслеників має велике значення і воно визначено багатьма стандартами.

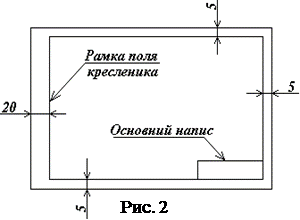
Зокрема, стандарти дозволяють контролеру повертати розроблювачу конструкторську документацію без розгляду у випадку недбалого її виконання. Це необхідно враховувати студентам при виконанні креслеників. Графічні роботи виконуються на креслярському папері формату А3(420x297мм). На кожному форматі, відповідно до ГОСТ 2.301-68, проводяться лінії рамки (рис. 2).

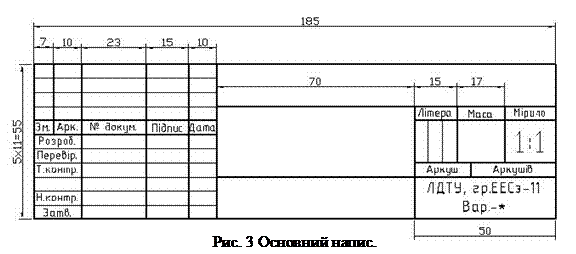
У правому нижньому куті формату міститься основний напис (штамп). Усі кресленики оформляють основним написом згідно з ГОСТ 2.104-68, розміри якого (55x185). У графах основного напису (номери граф на рис. 3 поміщені в лапки) вказується:

– назва кресленика відповідно до змісту роботи;

– назва вузу, групи;

– номер варіанта;

– шифр студента (№ залікової книжки);

– прізвище;

– підпису осіб, прізвища яких зазначені в графі 5;

– дата підписання;

– мірило зображення;

– порядковий номер аркуша;

– загальна кількість аркушів у роботі.

Написання букв і цифр повинно відповідати ГОСТ 2.304-81.

Товщина і тип ліній беруться відповідно до ГОСТ 2.303-68. Умови задач, усі геометричні побудови виконуються за допомогою креслярських інструментів, олівцем, спочатку тонкими лініями (0,3 мм), а потім лінії видимого контуру обводяться суцільною основною лінією товщиною 0,5-1,4 мм, лінії невидимого контуру - штриховою 0,3-0,5 мм, всі інші тонкі - 0,3 мм. Надписи та літери на аркушах виконуються стандартним шрифтом за ГОСТ 2.304-81. Висота цифр повинна бути не менше 3,5 мм. Кресленики та рисунки повинні бути виконані за розмірами, зазначеним у завданнях.

Завдання №1

Тема:	Епюр Монжа. Побудова ламаної за координатами точок.
Мета:	Навчитись будувати проекції та наочні зображення геометричних елементів координатним способом.
Зміст:	За варіантами табл. 7: 1. Побудувати три проекції ламаної АBCDEF (рис. 9). 2. Побудувати наочне зображення ламаної АBCDEF (косокутну диметричну проекцію), розмістивши всі точки на ребрах умовного паралелепіпеда (рис. 10). 3. Позначити видимість ланок ламаної (штриховими лініями) відносно граней паралелепіпеда (рис. 10). 4. Визначити розташування ланок ламаної відносно площин проекцій П1,П2,П3 (таблиця рис. 10). 5. Приклад виконання завдання (рис. 11)

Методика виконання завдання. Проекції точок на площинах проекцій будуються за двома координатами: П₁ – (х; y), П₂ – (х; z), П₃ – (y; z). У горизонтальній площині проекцій (П₁)за додатній напрямок осей приймають: для осі x – вліво від початку координат, для y – вниз; у фронтальній площині (П₂):додатній напрямок x – вліво, z – вгору; у профільній площині (П₃): додатній напрямок y – вправо, z – вгору.Для позначення додатного напрямку на кінцях осей використовують стрілки.

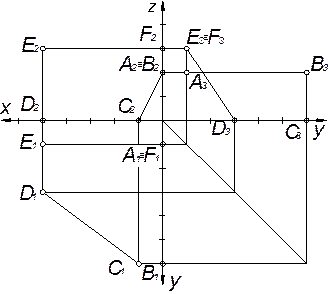Рис. 9

Накреслимо осі координат, побудуємо, проекції точки A(0;10;20) (рис.9). Так як координата х для цієї точки рівна нулю, її проекції А₁ і А₂ знаходяться на осі yz, а проекція А₃ на полі П₃.

Аналогічно будуємо проекції інших точок B (0;60;20), С(10; 60; 0), D(50; 30; 0), Е (50;10;30), F (0;10;30).

Для побудови наочного зображення використаємо косокутну диметричну проекцію, положення аксонометричних осей якої представлено на рис. 10, (де кут між додатнім напрямом осей х і у складає 45º, а між х і z – 90º). У цій системі координат по осях х i z встановлено масштаб 1:1, по осі у – 1:2. За координатами точок, використовуючи лінії зв’язку, будуємо їх проекції (рис. 10). Наочне зображення точки отримаємо, провівши взаємно перпендикулярні лінії зв’язку із кожної її проекції (рис. 10). Аналогічно будуємо наочні зображення всіх інших точок B, С, D, Е, F (рис. 10).

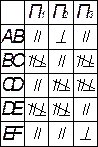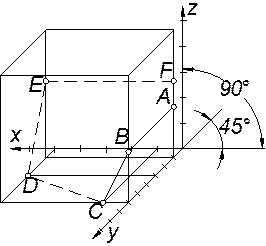Рис. 10

З’єднуємо послідовно точки А, В, С, D, Е і F, та отримаємо ламану лінію, відрізки якої в просторі можуть займати як загальне, так і окреме положення. Аналізуємо положення відрізків ламаної по відношенню до площин проекцій, результати зводимо до таблиці. Приклад виконання завдання зображено на рисунку 11.

Рис. 11

Таблиця 7

Завдання 2.Тема: Знаходження величини двогранного кута при ребрі SB (метод плоскопаралельного переміщення).

Завдання. 3.Тема: Визначити відстань між мимобіжними ребрами SA і ВС (метод заміни площин проекцій).

Зміст завдань

Задані координати вершин піраміди SАВС.

Визначити:

1. Величину двогранного кута при ребрі SB (метод плоскопаралельного переміщення).

2. Визначити відстань між мимобіжними ребрами SA і ВС(метод заміни площин проекцій).

Т Точки	X	Y	Z
А
В
С
S

Мета завдання– практично застосувати отримані знання, розвинути графічні навички і просторову уяву. В інженерній практиці трапляються задачі на визначення натуральних величин відрізків, кутів, фігур, що займають загальне положення відносно площин проекцій. Розв’язок таких задач виконується перетворенням вихідного креслення так, щоб елементи загального положення зайняли часткове положення. Задачі, що розв’язуються за допомогою методів перетворення, зводяться до чотирьох основних задач: пряму загального положення перетворити в пряму рівня, пряму рівня перетворити в проектуючу пряму, площину загального положення перетворити в проектуючу площину, проектуючу площину перетворити в площину рівня.

Варіанти завдань подані в таблиці 1.

Основні теоретичні положення.

До задачі 1. Плоскопаралельне переміщення.

Проекція заданого предмета на площину, паралельно якій проходить переміщення його точок, зберігає свої розміри і форму, змінюючи тільки положення відносно ліній зв’язку.

До задачі 2. Заміна площин проекцій.

Заданий об’єкт у просторі залишається нерухомим. Одна з площин проекцій замінюється новою площиною, яка стане в необхідне положення і буде перпендикулярною до основної площини проекцій. Можлива послідовна заміна обох площин проекцій.

Варіанти завдань до епюрів № 2 та 3

Таблиця 3

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

X

Y

Z

X

Y

Z

X

Y

Z

X

Y

Z

A

A

A

A

B

B

B

B

C

C

C

C

S

S

S

S

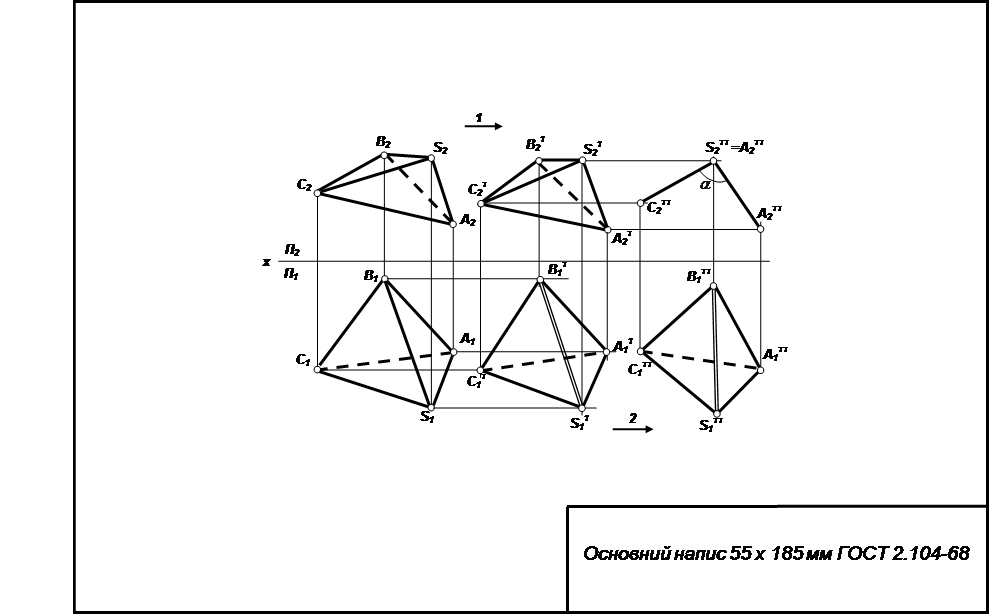
Зразок виконання роботи подано на рис. 6, 7, 8.

Питання для самоконтролю

1. Як повинен бути розташований трикутник АВС, щоб він проектувався на площину в натуральну величину?

2. Як виконується плоскопаралельне переміщення зображення?

3. Як перетворити площину трикутника загального положення у проектуюче?

4. Як перетворюється горизонталь на площині П₁ іП₂?

5. Яким чином вибираються площини П₄ і П₅?

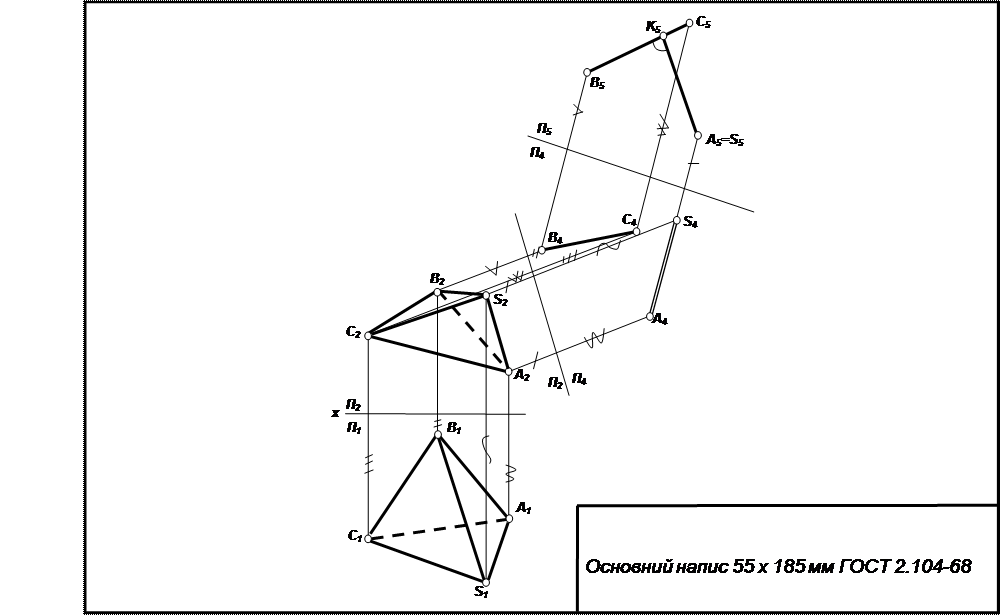
Методика виконання завдання.

Методична карта 1

Визначити величину двогранного кута при ребрі SB (метод плоско-паралельного переміщення).

1. Обертання проводиться на площині П₂ навколо невиявленої осі.

Ребро BS ║ П₁ (переміщення довільне). B₂S₂ ║ х, B₁¹S₁¹– натуральна величина. S₂A₂B₂C₂=S₂¹A₂¹B₂¹C₂¹. Проекція S₁¹A₁¹B₁¹C₁¹ будується по лініях зв’язку.

2. Обертання проводиться на площині П₁. B₁¹S₁¹ ┴ П₂. Визначається положення S₂¹¹A₂¹¹B₂¹¹C₂¹¹. S₂¹¹ ≡ B₂¹¹.

Кут C₂¹¹B₂¹¹A₂¹¹ – шуканий.

Методична карта 2

Визначити відстань між мимобіжними ребрами SA і ВС (метод заміни площин проекцій).

Проводиться заміна площин проекцій П₁ на П₄ ┴ П₂. Площина П₄ ║ SA.

S₄A₄=SA – натуральна величина на площині П₄.

В₄С₄ – проекція ребра ВС загального положення.

Проводиться заміна площини П₂ на П₅ ┴ П₄. П₅ ┴ SA.

Ребро SA проектується в точку на площині П₅. S₅ ≡ A₅.

Відрізок SK – шукана відстань. SK ┴ ВС.

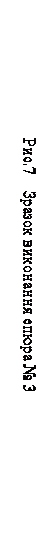
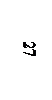
Лист 5

Завдання для виконання 2D креслень

В CAD-програмах

(робота №2)

На сьогоднішній день AutoCAD – найбільш поширена система автоматизованого проектування з тих, що працюють на ПК. Вона здатна виконувати всі види креслярських робіт, необхідних у найрізноманітніших формах технічного проектування.

Рекомендації до виконання роботи

Студенту, в процесі навчання, необхідно виконати кресленик плоскої деталі в AutoCAD.

Для цього формат А3 розкреслюється на дві частини. Зліва викреслюється рамка та основний напис по розміру формату А4. На ньому, згідно завдання взятого з рис.6, виконується кресленик деталі “в олівці” так, щоб вона займала близько 70% вільного місця. Приймається мірило 1:1 і проставляються розміри деталі.

Для виконання рисунків в AutoCAD студенти користуються методичними вказівками до лабораторних занять на тему: “Застосування 2D геометричного моделювання у програмі AutoCAD” Луцьк – 2003., та електронним підручником, який встановлений у комп’ютерному класі кафедри ІКГ.

Файл виконання кресленика, формату *.dwg необхідно розмістити в персональну папку, яку студенти створюють під час практичних занять в лабораторії комп’ютерної графіки.

Якщо використовується програмне забезпечення та техніка поза межами університету то слід звернути увагу на сумісність програмного забезпечення. Тобто, вищеназваний файл повинен бути збережений для використання у AutoCAD 2000.

Варіанти завдань представлені на рис.6.

Зразок готового графічного завдання до роботи № 2 представлений на рис.7.

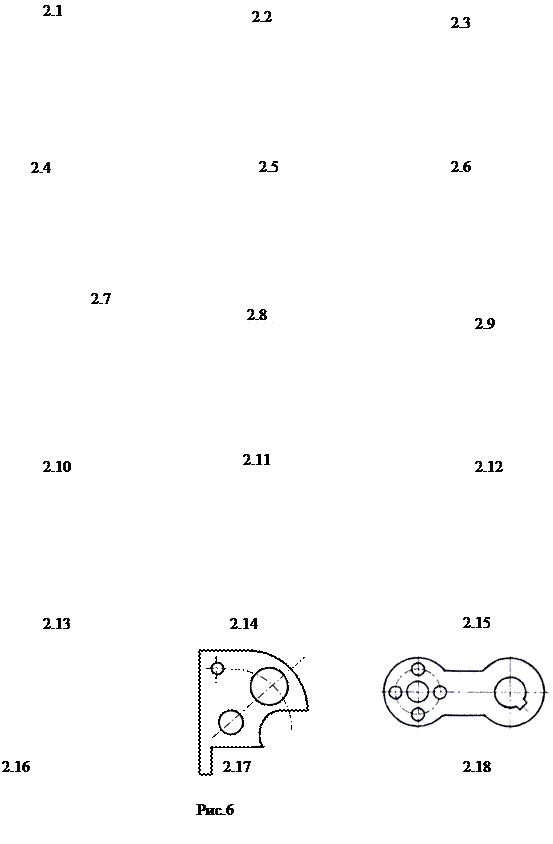
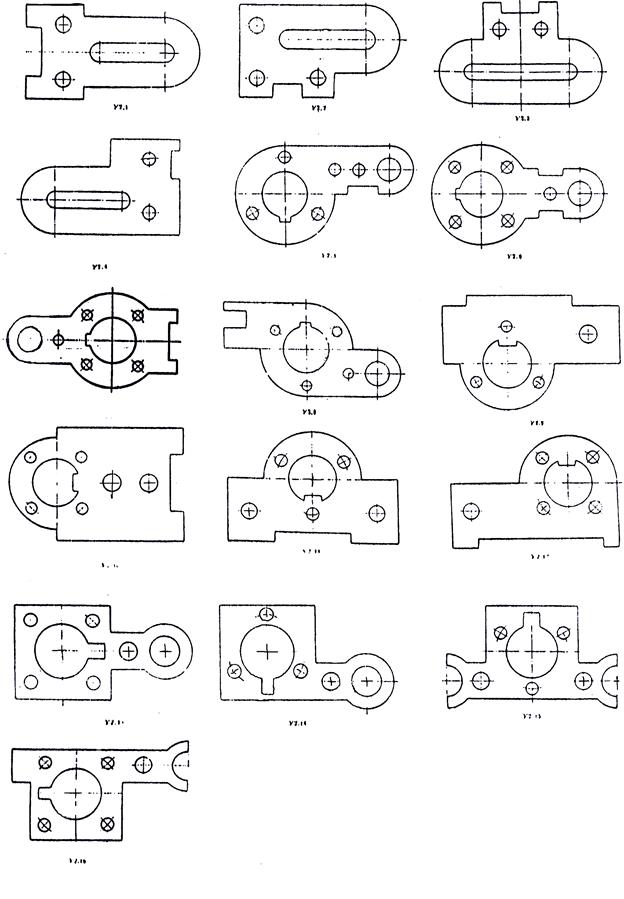
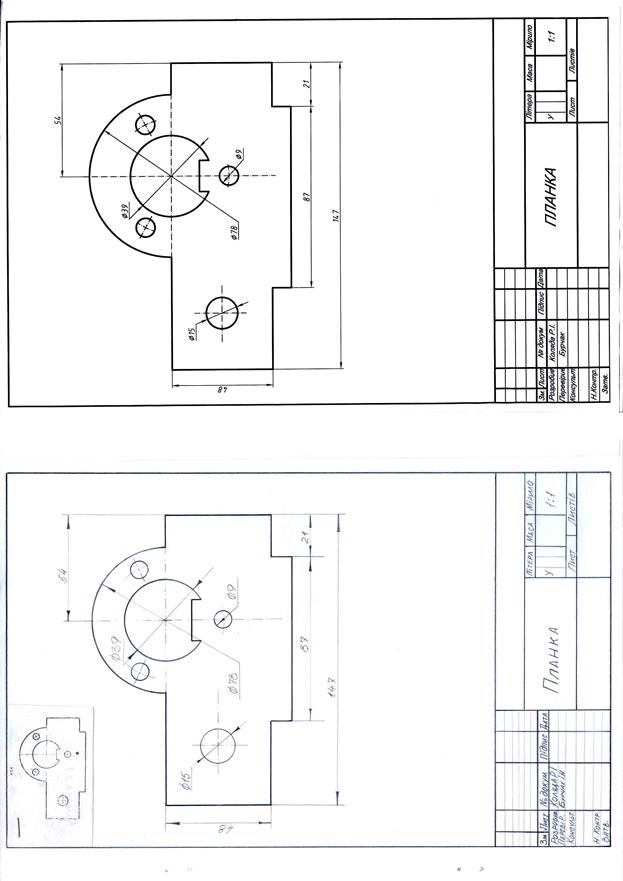
Рис.7

6. Завдання для виконання 3D твердотільної моделі

В CAD-програмах

(робота №3)

Рекомендації до виконання роботи

Побудувати вигляди та аксонометричну проекцію предмета за його описом. Предмет виконати з двома отворами – призматичним і циліндричним.

За описом, який наведено в таблиці 1, в просторі Model слід створити модель геометричного тіла (правильної форми) з вертикальним циліндричним і горизонтальним призматичним отворами (параметри отвору в таблиці 2).

У просторі Layout побудувати головні види (спереду, зверху і зліва) та аксонометричну проекцію з вирізом 1/4 частини предмета, яка найближча до спостерігача. На виді спереду і виді зліва слід виконати вид в сполученні з розрізом, розміщуючи з лівої сторони вид, а з правої – розріз (відповідно до вимог державного стандарту). На виді зверху розріз слід теж зробити і розмістити його в нижній частині цього зображення. Далі необхідно нанести розміри у відповідності до ГОСТ 2.307-68, звертаючи увагу на те, щоб розміри не повторювались на різних зображеннях і були характерними для параметрів геометричної поверхні.

Таблиця 1

Опис геометричної поверхні

№ варіанта	Зовнішня форма поверхні	Циліндричний вертикальний отвір
1, 19, 28	Шестикутна правильна призма. Діаметр кола, який описаний навколо шестикутника основи, дорівнює 90 мм. Дві вершини основи розміщені на горизонтальній осі симетрії. Висота призми – 100 мм.	Наскрізний отвір діаметром 30 мм. Вертикальна вісь проходить через центр шестикутника
2, 18, 29	П’ятикутна правильна призма. П’ятикутник основи вписаний в коло діаметром 90 мм. Одна з вершин п’ятикутника розміщена на вертикальній осі симетрії основи і є найближчою до спостерігача. Висота призми – 100 мм.	Наскрізний отвір діаметром 30 мм. Вертикальна вісь проходить через центр п’ятикутника.
3, 17, 25	Чотирикутна правильна призма. Сторона основи квадрата – 70 мм. Вершини квадрата розміщені на горизонтальній і вертикальній осях симетрії основи. Висота призми – 100 мм.	Наскрізний отвір діаметром 25 мм. Вертикальна вісь проходить через центр квадрата.
4, 16, 24	Прямий круговий циліндр. Діаметр основи – 90 мм. Висота циліндра – 100 мм.	Вертикальний отвір діаметром 25 мм проходить до верхньої площини призматичного отвору.
5, 15, 23	Сфера діаметром 100 мм. На висоті 80 мм зрізана горизонтальною площиною.	Наскрізний отвір діаметром 30 мм. Вісь отвору збігається з вертикальною віссю сфери.
6, 14, 22	Чотирикутна правильна призма. Сторона основи квадрата – 70 мм. Вершини квадрата розміщені на горизонтальній і вертикальній осях симетрії основи. Висота призми – 100 мм.	Наскрізний отвір діаметром 30 мм. Вертикальна вісь отвору проходить через центр квадрата.

Продовження таблиці 1

7, 13, 21	Шестикутна правильна призма. Діаметр кола, який описаний навколо шестикутника основи, дорівнює 80 мм. Дві вершини основи розміщені на горизонтальній осі симетрії. Висота призми – 100 мм.	Наскрізний отвір діаметром 25 мм. Вертикальна вісь отвору проходить через центр шестикутника.
8, 12, 20	Сфери діаметром 100 мм. На висоті 80 мм зрізана горизонтальною площиною.	Наскрізний отвір діаметром 25 мм. Вісь отвору збігається з вертикальною віссю сфери.
9, 11, 26	П’ятикутна правильна призма. П’ятикутник основи вписаний в коло діаметром 90 мм. Одна з вершин п’ятикутника розміщена на вертикальній осі симетрії основи і є найближчою до спостерігача. Висота призми – 100 мм.	Наскрізний отвір діаметром 25 мм. Вертикальна вісь проходить через центр п’ятикутника.
10, 27, 30	Прямий круговий циліндр. Діаметр основи – 90 мм. Висота циліндра – 100 мм.	Вертикальний отвір діамет­ром 30 мм проходить до верхньої площини призматичного отвору.

Завдання слід виконати на аркуші формату А3 (420х297 мм). Приклад виконання наведено на рис. 8.

Таблиця 2

Розміри призматичного отвору

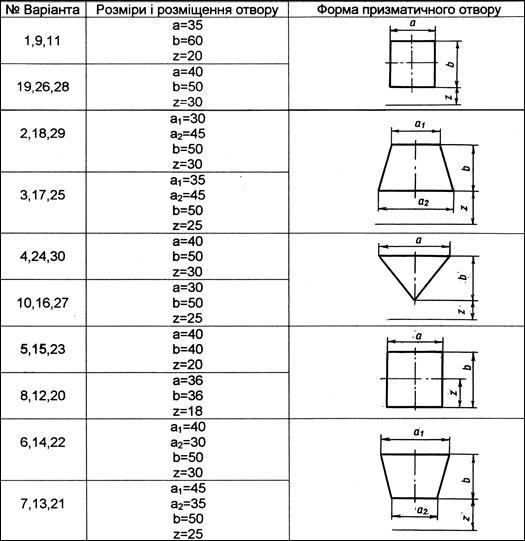
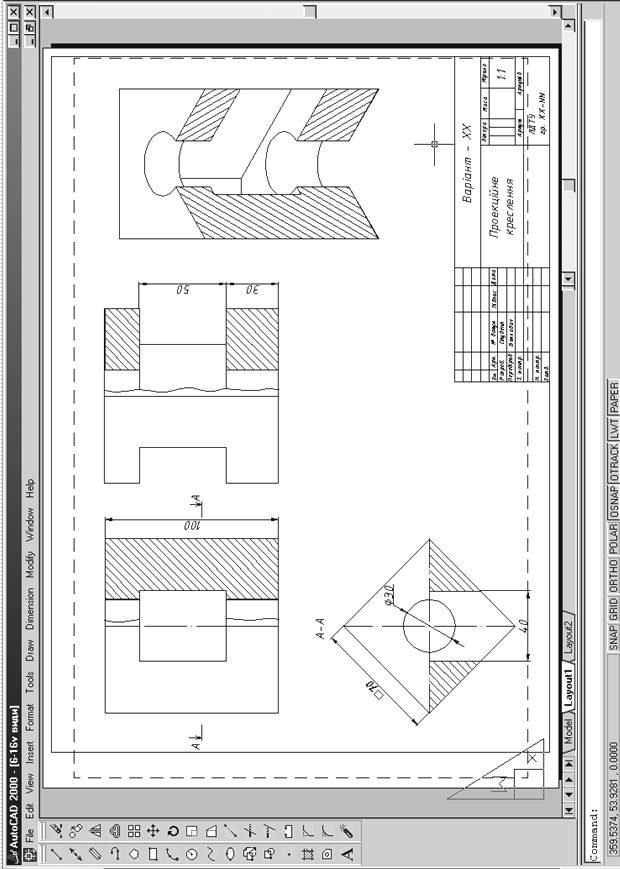
Рис.8

Список рекомендованої літератури

1. Бурчак І.Н., Місюк В.М., Сидорук А.М. Методичні вказівки до лабораторних занять на тему: “Застосування 2D геометричного моделювання у програмі AutoCAD”. – Луцьк.: РВВ ЛДТУ, 2003. – 46 с.

2. 3D геометричне моделювання в середовищі AutoCAD. Методичні вказівки до лабораторних занять. Для студентів технічних спеціальностей денної та заочної форм навчання. Величко В.Л.-Луцьк: РВВ ЛДТУ, 2006. – 58 с.

3. Растрова графіка. Методичні вказівки до лабораторних занять. Для студентів технічних спеціальностей денної та заочної форм навчання. Величко В.Л.-Луцьк: РВВ ЛДТУ, 2007. – 40 с.

4. Михайленко В.Є., Найдиш В.М., Підкоритов А.М., Скидан I.А. Інженерна та комп’ютерна графіка: Підручник; За ред. В. Є. Михайленка. – К.: Вища шк., 2000. – 342 с.

5. Михайленко В.Є., Пономарьов А.М. Інженерна графіка. – К.: Вища шк., 1986 – 286 с.

6. Геометрическоемоделирование и машинная графика в САПР: Учебник / В.Е.Михайленко, В.Н.Кислоокий, А.А.Лященко и др.- К.-: Выща шк., 1991. – 374 с.: ил.

7. Основи комп’ютерної графіки: У 2-х кн. Навчальний посібник для студентів вищих навчальних закладів / Г.В.Веселовська, В.Є.Ходаков, В.М.Веселовський; під ред.В.Є.Ходакова.- Херсон: “Олді-плюс”, 2001.-216 с.;іл..95.

8. Порев В.Н. Компьютерная графика.-СПб.:БХВ-Петербург,2002.
-432 с.:ил.

9. Михайленко В.Е., Ковалёв С.Н., Седлецкая Н.И. и др. Инженерная геометрия с элементами теории параметризации – К.: УМК ВО, 1989. – 83c.

10. Единая система конструкторской документации.

11. Островський О. Інженерне креслення з додатком основ комп’ютерного креслення (CAD). – Львів.: Оксарт, 1998. – 184 с.

12. Ковальов С.М.,Гумен М.С.,Пустюльга С.І.,Михайленко В.Є.,Бурчак І.Н Прикладна геометрія та інженерна графіка. Спеціальні розділи. Випуск 1. – Луцьк: Редакційно-видавничий відділ ЛДТУ, 2006. – 256 с.

13. Ванін В.В., Перевертун В.В., Надкернична Т.О. Комп’ютерна графіка в середовищі AutoCAD: Навч. посібник. – К.: Каравела, 2006. – 336 с.

Зміст

Вступ
1. Графічні роботи.
2. Титульний лист.
3. Вимоги до оформлення самостійних та індивідуальнихробіт.
4. Епюр Монжа. Побудова ламаної за координатами точок.
5. Визначити величину двогранного кута при ребрі SB (метод плоско-паралельного переміщення).
6. Визначити відстань між мимобіжними ребрами SA і ВС (метод заміни площин проекцій).
7. Завдання для виконання 2D креслень в CAD-програмах.
8. Завдання для виконання 3D твердотільної моделі в CAD-програмах.
Список рекомендованої літератури.

НАВЧАЛЬНО-МЕТОДИЧНЕ ВИДАННЯ

Методичні вказівки до самостійної роботи для студентів напряму підготовки 0505 „Машинобудування” скороченого терміну денної та заочної форм навчання з дисципліни „Нарисна геометрія, інженерна та комп’ютерна графіка”. / Бурчак І. Н., Клак Ю.В. - Луцьк: РВВ ЛДТУ, 2014.- 28 c.

Комп’ютерний набір та верстка: І.Н.Бурчак, Ю.В. Клак.

Редактор:

Підп. До друку ________Формат 60х84/16. Папір офс.

Гарн. Таймс. Ум. друк. арк. ____. Обл. вид. арк. ___

Тираж ____ прим. Зам. ______

Редакційно-видавничий відділ

Луцького національного технічного університету

43018 м. Луцьк, вул. Львівська, 75.

Друк – РВВ ЛуцькогоНТУ