П. 6. Понятие о ранге матрицы
Матрица имеет много миноров, причем некоторые из них могут равняться нулю, а другие быть отличными от нуля. Замечание. Миноры существуют и для прямоугольных матриц. Они получаются путем вычеркивания нескольких строк и столбцов, лишь бы количество оставшихся строк равнялось количеству оставшихся столбцов, при этом порядок минора матрицы размера 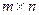 не превосходит меньшего из чисел m и n.
не превосходит меньшего из чисел m и n.
Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.
Определение 18. Наивысший из порядков миноров матрицы А, отличных от нуля, называется рангом матрицы А. Обозначение: rang A или r A.
Примеры.Найти ранг матрицы.
1. 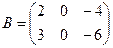 .
.
Решение. Найдем миноры 2-го порядка: 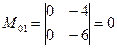 ,
, 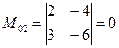 ,
, 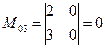 . Все определители второго порядка равны 0. Найдем миноры первого порядка: М2,23= 2 ≠ 0, следовательно, rang В = 1.
. Все определители второго порядка равны 0. Найдем миноры первого порядка: М2,23= 2 ≠ 0, следовательно, rang В = 1.
2. 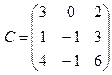 .
.
Решение. Так как матрица квадратная, то минором наивысшего порядка является определитель матрицы. Найдем его: 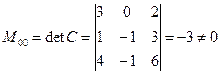 , следовательно, меньшие по порядку миноры можно не искать, наивысший (третий) найден, т.е. rang С = 3.
, следовательно, меньшие по порядку миноры можно не искать, наивысший (третий) найден, т.е. rang С = 3.
3. 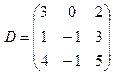 .
.
Решение. Так как матрица квадратная, то минором наивысшего порядка является определитель матрицы. Найдем его: 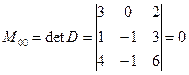 , следовательно, надо найти меньшие по порядку миноры.
, следовательно, надо найти меньшие по порядку миноры. 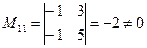 , минор второго порядка отличен от нуля, следовательно, rang D = 2.
, минор второго порядка отличен от нуля, следовательно, rang D = 2.
Определение 19. Строки матрицы А называются линейно зависимыми, если какая-либо из них линейно выражается через остальные. В противном случае – строки линейно независимы. (аналогично столбцы).
Пример. 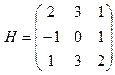 . Найти количество линейно независимых строк и столбцов.
. Найти количество линейно независимых строк и столбцов.
Решение.Обозначим строки: Е1 = (2 3 1), Е2 = (–1 0 1), Е3 = (1 3 2). Видно, что Е3 = Е1 + Е2, следовательно, Е1, Е2, Е3 – линейно зависимы. Е2 ≠ k Е1, следовательно, Е1 , Е2 – линейно независимы. Вывод: матрица имеет две линейно независимых строки.
Обозначим столбцы: F1, F2, F3. Видно, что F2 = F1 + F3, следовательно, F1, F2, F3 – линейно зависимы. F1 ≠ k F2, следовательно, F1, F2 – линейно независимы. Вывод: матрица имеет два линейно независимых столбца.
Можно доказать, что для любой матрицы максимальное число линейно независимых строк и максимальное число линейно независимых столбцов совпадают.
Определение 20.Ранг матрицы равен максимально возможному числу ее линейно независимых строк (столбцов).
Т.е. rang H = 2. Проверим первым способом. 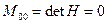 ,
, 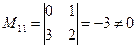 , т.е. rang H = 2.
, т.е. rang H = 2.
Замечание.Ранг квадратной матрицы не превосходит ее порядок. Ранг равен порядку в том и только в том случае, если матрица невырожденная. Ранг матрицы размера 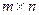 не превосходит меньшего из чисел m и n.
не превосходит меньшего из чисел m и n.
Не изменяют ранга элементарные преобразования над матрицами:
1. перестановка строк (столбцов),
2. умножение строки (столбца) на число, не равное нулю,
3. прибавление к строке (столбцу) другой строки (столбца), умноженной на число,
4. отбрасывание нулевых строк (столбцов),
5. транспонирование.
Если удастся путем элементарных преобразований привести матрицу к трапециевидной форме, то ееранг будет равен числу ее ненулевых строк!
При приведении матрицы к трапециевидной форме удобно пользоваться численным методом Гаусса:
1) переставляя строки, добиваемся, чтобы 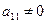 и
и 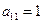 , последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на
, последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на 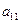 . Первую строку называют рабочей, а элемент
. Первую строку называют рабочей, а элемент 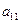 – ведущим.
– ведущим.
2) умножаем первую строку на числа ( 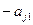 ), где
), где 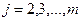 , прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под
, прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под 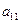 нули.
нули.
3) не трогая первой строки, добиваемся, чтобы 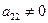 и
и 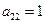 путем деления всей строки на
путем деления всей строки на 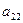 или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент
или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент 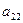 – ведущим.
– ведущим.
4) умножаем вторую строку на числа ( 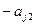 ), где
), где 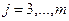 , прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под
, прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под 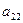 нули.
нули.
5) и т.д.
