Сравнение выборочных средних

Как правило, выборочные характеристикине совпадают по абсолютной величине с соответствующими генеральными параметрами. Величина отклонения выборочного показателя от его генерального параметра называется статистической ошибкой этого показателя или ошибкой репрезентативности. Статистические ошибки – это не ошибки, допускаемые при измерении биологических объектов. Они возникают исключительно в процессе отбора вариант из генеральной совокупности и к ошибкам измерений отношения не имеют.

Достоверность выборочных показателей устанавливают при помощи ошибки репрезентативности, или средней ошибки – (S_х) или (m_х), вытекающей из самой сущности выборочного обследования, при котором целое (генеральная совокупность) характеризуется на основании изучения части (выборки).

В малых выборках 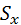вычисляется по следующей формуле:

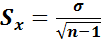; когда n < 30 , (5)

S_х – ошибка средней арифметической,

σ – среднее квадратическое отклонение,

n - количество признаков (вариант).

Согласно этой формуле, ошибка средней арифметической зависит от величины σ и n, причем, чем меньше разнообразие признака, тем меньше ошибка. При полной однородности совокупности по изучаемому признаку (σ = 0) средняя ошибка равна нулю, т.е. Х выборки становится равной Х генеральной совокупности. Величина средней ошибки находится в обратной зависимости от n. Чем больше вариант вошло в выборку, тем меньше ошибка выборочной Х. Допустим, в выборке из 30 коров среднесуточный удой – Х = 21,26 кг, а σ = ±3,68. Ошибка средней арифметической в данном случае составит:

= 0,68 кг

Это обозначает, что средняя ошибка на 30 голов составляет 0,68 кг. Следовательно, среднесуточные удои изученной выборки характеризуются Х ± S_х = 21,6 ± 0,68.

При больших вариационных рядах количество арифметических действий достигает многих десятков и даже сотен, что нередко ведет к, так называемым, ошибкам внимания. Существует более простой метод вычисления статистической ошибки средней арифметической, который дает возможность в несколько раз сократить количество арифметических действий и снизить при этом вероятность ошибок внимания.

Предлагаемый метод называется константный метод вычисления ошибки средней арифметической по формуле Петерса и константе Молденгауэра. Этот метод раньше применялся в биологических исследованиях, его использовал Е.В.Монцевичуте – Эрингене в работах по медицинской онкологии. Однако он не получил до сих пор широкого применения и не описывается в руководствах по биометрии.

Ошибку средней арифметической вычисляют константным методом по формуле:

S_х (m) = К × Σ а,(6)

где К – константа Молденгауэра, вычисленная по формуле

К = , (7)

Σ –знак суммы, а – отклонения вариантов от средней арифметической (х – Х). В табл. 4 представлены вычисленные константы от различного количества вариант от 3 до 101 по порядку, а затем через каждые 50 до 1000.

Ход вычисления прост. После определения средней арифметической величины (Х = Σх : n) находят от неё отклонения (а) для каждого варианта. Последние суммируют без учета арифметических знаков и полученную сумму умножают на константу в таблице 4 в строке соответствующего количества вариант или близкой к нему. В результате получают значение статистической ошибки средней арифметической величины.

Таблица 4 -Константы Молденгауэра для вычисления ошибок

Средних арифметических

Число вариант	Конс-танты	Число вариант	Конс-танты	Число вариант	Конс-танты	Число вариант	Конс-танты
	0,2904		0,0096		0,0037	93-96	0,0014
	0,1809		0,0091		0,0036	97-100	0,0013
	0,1253		0,0086		0,0035		0,0012
	0,0934		0,0082		0,0034		0,00062
	0,0731		0,0078		0,0033		0,00045
	0,0592		0,0074		0,0032		0,00032
	0,0492		0,0070		0,0031		0,00024
	0,0418		0,0067		0,0030		0,00019
	0,0360		0,0064	57-58	0,0029		0,00016
	0,0315		0,0062		0,0028		0,00013
	0,0278		0,0059	60-61	0,0027		0,000107
	0,0248		0,0056		0,0026		0,000097
	0,0223		0,0054	63-64	0,0025		0,000085
	0,0202		0,0052	65-66	0,0024		0,000076
	0,0184		0,0050	67-68	0,0023		0,00068
Продолжение таблицы 4
	0,0169		0,0048	69-70	0,0022		0,000061
	0,0156		0,0047	71-72	0,0021		0,000055
	0,0144		0,0045	73-74	0,0020		0,000050
	0,0133		0,0043	75-77	0,0019		0,000046
	0,0124		0,0042	78-80	0,0018		0,000043
	0,0110		0,0040	81-83	0,0017		0,000040
	0,0102		0,0039	84-87	0,0016	-	-
	0,0099		0,0038	88-92	0,0015	-	-

Таким образом, константный метод не требует возведения в квадрат каждого отклонения от средней арифметической (или самих вариант) и вычисления квадратного корня.

Пример. Вычислить среднюю арифметическую величину и ее статистическую ошибку следующего вариационного ряда.

Варианты (х)											Σ х = 130
Отклонения а = х - Х											Σ а = 12

При n = 10 средняя арифметическая равна Х = 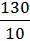= 13,0

Константа Молденгауэра (К) при десяти вариантах равна 0,0418. Подставляем в формулу Петерса:

S_х = К × Σ а = 0,0418 × 12 = 0,5016 ≈ 0,5

Таким образом, данный вариационный ряд характеризуется

Х ± S_х = 13,0 ± 0,50