Теория мономолекулярной адсорбции Ленгмюра
Рассмотрим основные положения мономолекулярной адсорбции, которая была развита в 1915 г. И. Ленгмюром.
1. На поверхности адсорбента имеются локализованные адсорбционные центры. Ими могут быть дефекты кристаллической поверхности – грани кристаллов, механические дефекты, микротрещины, углубления, вкрапления тяжёлых металлов, определённые функциональные группы (гидроксильные, карбоксильные, фосфатные, карбамидные и т. д.).
2. Адсорбция является мономолекулярной, т. е. в локализованном центре может находится только одна молекула адсорбата или не одной.
3. Процесс адсорбции является обратимым и равновесным – адсорбированная молекула удерживается активным центром некоторое время, после чего десорбируется; таким образом, через некоторое время между процессами адсорбции и десорбции устанавливается динамическое равновесие.
4. Адсорбционные центры не взаимодействуют между собой, т.е. они «работают» независимо друг от друга.
Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, связанные с ограниченностью адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
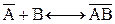 | (5.3) |
где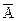 
– адсорбционные центры поверхности; В – распределяемое вещество; 
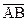– образующийся комплекс на поверхности.
По мере увеличения концентрации вещества В реакция сдвигается в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия
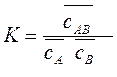 | (5.4) |
В этом соотношени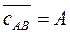и
 и 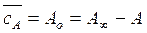 | (5.5) |
где А – величина адсорбции;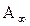 
– емкость адсорбционного монослоя; 
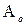–число оставшихся свободными адсорбционных центров, приходящихся на единицу площади поверхности или на единицу массы адсорбента.
Подставляя уравнение (5.5) в уравнение (5.4) , получаем:
,
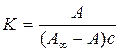или
.
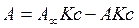Окончательно имеем:
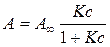 | (5.6) |
Выражение (5.6) называется уравнением изотермы Ленгмюра.
При описании процесса адсорбции газов в уравнении (6) концентрация может быть заменена пропорциональной величиной парциального давления газа:
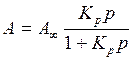 | (5.7) |
Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра (К и Кр) характеризует энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия.
 |  |
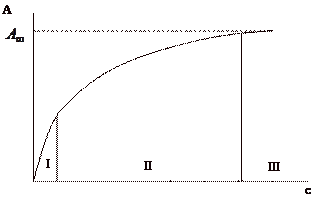Изотерма адсорбции, рассчитанная по уравнению Ленгмюра, как видно из рис. Является параболой. Величина 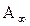соответствует максимальному заполнению поверхности монослоем адсорбированного вещества. Возможны следующие ситуации.
1. При малых концентрациях или давлениях, когда с→0 получаем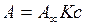 
. Уравнение Ленгмюра принимает вид, тождественный уравнению Генри: величина адсорбции линейно растёт с увеличением концентрации. Этот случай соответствует начальному, прямолинейному участку изотермы (I).
2. Концентрация (давление) адсорбтива имеет промежуточное значение – выполняются уравнения (6), (7). Адсорбция описывается переходным участком (II) изотермы.
3. При больших концентрациях и давлениях, когда Кс>>1 и Кр>>1 уравнения (6) и (7) переходят в соотношение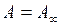 
. Адсорбция описывается графиком, параллельным оси абсцисс (III), что соответствует максимальному заполнению поверхности слоем адсорбированного вещества.
Для графического решения (с целью определения констант 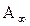и К) уравнение Ленгмюра с помощью элементарных преобразований приводим к линеаризованному виду:
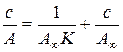 . | (5.8) |
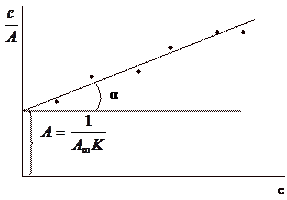
Полученное уравнение является уравнением прямой в координатах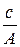 
от с (рис. ). Экстраполяция зависимости до оси ординат даёт отрезок, равный 
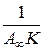, а тангенс угла наклона прямой α равен 
.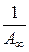