Диаграмма состава сополимеров
Зависимость состава сополимеров от состава смеси мономеров удобно характеризовать диаграммой состав мономерной смеси – состав сополимеров (рис.4.1). Форма получаемых кривых (1-5) зависит от значения r1 и r2. При этом возможны следующие случаи:
1)r1 = r2 = 1 т.е. для всех соотношений концентрации мономеров в реакционной смеси состав сополимеров равен составу исходной смеси;
2)r1 > 1; r1 < 1 для всех соотношений мономеров в исходной смеси сополимер обогащен звеньями M1 (r1 > 1 значит k11 > k12; r2 < 1 значит k22 > k21);
|
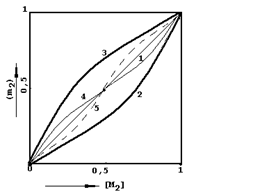 |
3)r1 < 1; r2 > 1, для всех исходных соотношений концентрации мономеров сополимеров обогащен звеньями M2 (r1 < 1 значит k11 < k12; r2 > 1 значит k22 > k21);
4)r1 < 1и r2 < 1, т.е. при малых содержания M1в исходной смеси мономеров сополимер обогащен звеньями M1, а при больших – звеньями M2, другими словами M'1 легче реагирует с M2 а M'2 с M1.
5)Случай, когда r1 > 1 и r2 > 1, которому должна соответствовать тенденция к раздельной полимеризации мономеров в смеси, на практике не реализуется. M'1 легче реагирует с M1.
Значение констант сополимеризации позволяет определить состав сополимеров. При r1 * r2 = 1 процес называется идеальной сополимеризацией.
При r1 * r2 = 0 процесс называется чередующейся сополимеризацией, при которой растущая цепь, состоящая из звеньев мономера одного типа, соединяет молекулу другого мономера.
Схема “Q – e”.Реакционная способность мономеров существенно зависит от их строения. Взаимосвязь r1 и r2 с величинами, зависящими только от строения мономеров, установлена Алфреем и Прайсом. Авторами предложена эмпирическая схема “Q – e”, согласно которой
r1 = (Q1/Q2) exp [ - e1 (e1 – e2)] (6)
r2 = (Q2/Q1) exp [ - e2 (e2 – e1)] (7)
r1 * r2 = exp [ - (e1 – e2)] или ln r1 * r2 = - (e1 – e2) (8)
где Q1 и Q2 – величины, характеризующие реакционную способность соответствующего радикала и мономера; e2 и e1 – параметры, определяющие соответствующие радикалы и мономеры. С полярности молекул М и М' – ла.
Согласно приведенным уравнениям, произведение r1 * r2 будет тем меньше, чем больше различие в значениях e1 и e2. Уменьшение этой величины свидетельствует о повышении способности мономеров к сополимеризации.
Используя схему “Q – e”, можно оценить относительную реакционную способность мономеров и влияние полярных факторов на сополимеризацию мономеров. При этом за стандартный мономер был принят стирол с Q = 1 и e = -0,8. Схема “Q – e” имеет только эмпирический характер, однако на ее основе можно проводить качественный анализ влияния строения мономера на его активность, а также сравнительный анализ бинарной статистической сополимеризации классических систем.
Методы определения констант сополимеризации. Наиболее распространенным являются методы Майо – Лъюиса и Файнмана – Росса, которые могут использоваться при небольших степенях конверсии ( < 10 % ).
Метод Майо – Лъюиса. Для опредиления констант сополимеризации по этому методу используют уравнение (5), решая его относительно r2.
    | [M1] | [m2] | [M1] | ||||||||
   r2 = r2 = | * | ( 1 + | * | r1) - 1 | |||||||
   | [M2] | [m1] | [M2] |
| |||||||
Для нахождения r1 и r2 определяют составы сополимеров ([m1]и [m2]]) для различных соотношений мономеров в исходной смеси (не менее трех). Затем по уравнению (9) рассчитывают r2, задаваясь произвольно выбранными значениями r1. Каждая сопряженная пара значений [M1], [M2] с [m1], [m2] дает прямую линию в системе координат r1 и r2. По координатам точки пересечения нескольких прямых определяют константы r1 и r2. Вследствие погрешностей опытов и анализов ( на основании которых определяют [m1] и [m2] эти прямые, как правило, не пересекаются в одной точке, а ограничивают некоторую наиболее вероятную область значений r1 и r2, в которой можно рассчитать среднее значения.
Метод Фрайнмана – Росса. В этом случае уравнение состава сополимера (5) преобразуют к виду
| F | 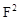 | |||||
 | (  f – 1) f – 1) | = r1 |  |
| ||
| f | f |

где F = [M1]/[M2] и f = [m1]/[m2]
По данным эксперимента строят график зависиZмости F/f (f-1) j от F2/f. Каждый опыт (т.е. пара значений F и f) дает точку на этом графике, а серия опытов прямую. Угловой коэффициент прямой соответствует значению r1 , а отрезок, отсекаемый на оси ординат, - значению r2 с обратным знаком.
