Многокомпонентная сополимеризация

Как уже упоминалось, в практическом отношении весьма важна терполимеризация, которая используется для придания сополимеру специфических свойств - сшиваемость, окрашиваемость, ударопрочность и т. п. В терполимеризации необходимо учитывать девять реакций роста цепи с участием трех типов активных центров:

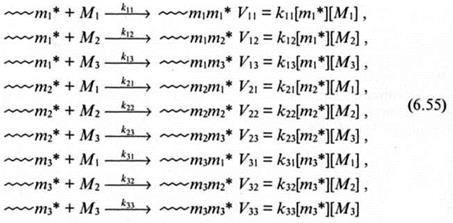
и шесть относительных активностей мономеров - констант сополимеризации:

Следует подчеркнуть, что константы относительной активности мономеров в терполимеризации являются константами бинарной сополимеризации, например:

Скорости исчерпания каждого из мономеров определяются суммой скоростей трех элементарных реакций:

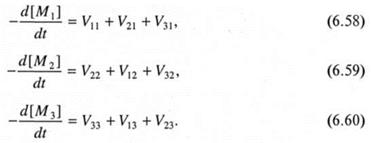
Предполагается, что терполимеризация, как и бинарная сополимеризация, быстро - за время, соизмеримое со временем жизни радикалов, - выходит на стационарный режим, для которого характерно постоянство активных центров каждого типа. Условие стационарности может быть выражено двумя путями. В первом случае приравниваются суммы скоростей реакций перекрестного роста:

Совместное решение (6.58) —(6.60) и (6.61) —(6.63) с использованием выражений для скоростей элементарных реакций приводит к весьма громоздкому уравнению состава:

Во втором случае условие стационарности выражается через равенство отдельных скоростей перекрестного роста:

В результате процедуры, описанной выше, получают более простое уравнение состава терполимера:

Таблица 6.2 Предсказанные и определенные экспериментально составы сополимеров, полученных радикальной тер- и тетраполимеризацией

Состав исходной смеси мономеров	Состав терполнмера, мол.%
система	Мономер	Содержание, мол.%	Определено экспериментально	Вычислено по уравнению
(6.64)	(6.66)
	Стирол Метилметакрилат Винилиденхлорид	31,24 31,12 37,64	43,4 39,4 17,2	44,3 41,2 14,5	44,3 42,7 13,0
	Метилметакрилат Акрилонитрил Винилиденхлорид	35,10 28,24 36,66	50,8 28,3 20,9	54,3 29,7 16,0	56,6 23,5 19,9
	Стирол Акрилонитрил Винилиденхлорид	34,03 34,49 31,48	52,8 36,7 10,5	52,4 40,5 7,1	53,8 36,6 9,6
	Стирол Метилметакрилат Акрилонитрил	35,92 36,03 28,05	44,7 26,1 29,2	43,6 29,2 26,2	45,2 33,8 21,0
	Стирол Акрилонитрил Винилиденхлорид	20,00 20,00 60,00	55,2 40,3 4,5	55,8 41,3 2,9	55,8 41,4 2,8
	Стирол Метилметакрилат Акрилонитрил Винилиденхлорид	25,21 25,48 25,40 23,91	40,7 25,5 25,8 8,0	41,0 27,3 24,8 6,9	41,0 29,3 22,8 6,9

Уравнение (6.66) можно получить статистическим методом, используя «правило произведения вероятностей». Исходя из (6.65), можно записать:

что приводит к

Переходные вероятности в терполимеризации выражаются обычным образом - через отношение скорости роста рассматриваемой реакции к сумме скоростей роста всех возможных реакций роста с участием данного типа активных центров. Уравнение состава, получаемое статистическим методом, идентично уравнению (6.66). Оба уравнения состава терполимера приводят к одинаковым результатам, о чем можно судить по данным табл. 6.2.

Как кинетическим, так и статистическим методом могут быть получены уравнения состава сополимера для более сложных систем, включающих четыре и более мономеров. Константы сополимеризации в этих уравнениях также являются относительными активностями бинарной сополимеризации.